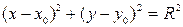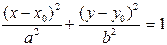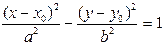Для практики большое значение имеют линии, которые в прямоугольной системе координат описываются алгебраическими уравнениями второй степени
Ax2 + B xy + C y2 + Dx + Ey + F = 0 (11)
причем хотя бы один из коэффициентов А, B, С должен быть не равен нулю. Рассмотрим наиболее важные частные случаи уравнения (11).
Окружность. Окружностью называется геометрическое место точек равноудаленных от данной точки, называемой центром окружности.
Уравнение окружности радиуса R с центром в точке M(а,b) имеет вид
(x - a)2 + (y - b)2 = R2 (12)
Если раскрыть скобки, то мы увидим, что уравнение (11) получается из уравнения (12), если A = C = 1, B = 0, D = -2a, E = -2b, F = - R2 + a2 + b2.
Пример. Пусть задано уравнение х2 + y2 - 4x = 0. Является ли это уравнение уравнением окружности и, если да, то каков ее радиус и координаты центра? Решение. Приведем данное уравнение к виду (12). Выделим полный квадрат относительно х, прибавляя и вычитая число 4.
x2 + y2 - 4x = (x2 - 4x + 4) + y2 - 4 = 0 или (x - 2)2 + y2 = 22. (13)
Сравнивая (12) с (13), видим, что заданное уравнение есть уравнение окружности радиусом R =2 и с центром в точке M с координатами а = 2, b = 0.
Эллипс. Эллипс - замкнутая кривая, для всех точек которой сумма расстояний до двух фиксированных точек, называемых фокусами эллипса, одинакова и равна, по определению, 2а. Для эллипса, представленного на рис.19, сумма расстояний MF1 и MF2 равна сумме расстояний NF1 и NF2 и равна 2а. Каноническое уравнение эллипса, центр симметрии которого находится в начале координат, а фокусы лежат на оси ОХ симметрично относительно оси OY
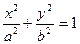 (14)
(14)
Параметры a и b называются его полуосями. Уравнение (11) получим из (14) если B = D = E = 0, A = 1/a2, C = 1/b2, F = -1. Очевидно, что окружность - частный случай эллипса, у которого a = b = R, а центр находится в начале координат.
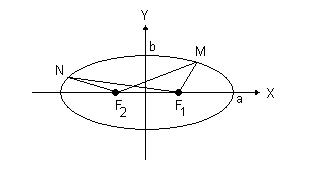
Рис. 19. Эллипс
Гипербола. Гипербола – неограниченная кривая, для всех точек которой разность расстояний до двух фиксированных точек, называемых фокусами, есть величина постоянная (рис. 20). Разность MF2 – MF1 равна разности NF1 – NF2 и по определению равна 2а. Каноническое уравнение гиперболы, центр симметрии которой совпадает с началом координат, а фокусы лежат на ост OX симметрично оси OY
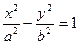 , (15)
, (15)
Параметры а и b называются полуосью и мнимой полуосью гиперболы. Уравнение (11) получим из (15) если B = D = E = 0, A =1 /a2, C = (-1)/b2, F = -1. Особенность гиперболы – наличие асимптот - прямых к которым неограниченно приближается кривая при 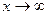 . Уравнения асимптот
. Уравнения асимптот 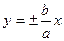 .
.

Рис. 20. Гипербола
Парабола. Парабола - неограниченная кривая, все точки которой (см. рис.21) равноудалены от точки, называемой фокусом и прямой, называемой директриссой. Для параболы изображенной на рис. 21 расстояния MK = MF, NF = NL и DO = OF. Каноническое уравнение параболы, ось которой совпадает с осью ОХ, а вершина лежит в начале координат
y2 = 2px, (16)
Уравнение (11) получим из (16) если A = B = E = F = 0, C = 1, D = -2p.

Рис. 21. Парабола.
Сделав поворот и сдвиг системы координат любое уравнение (11) можно привести только к одному из трех уравнений второй степени: (13-15) или к уравнению вида а2 х2 = b2 y2 , которому соответствуют две прямые. Это означает, что уравнениями второй степени можно описать только эллипс (и его частный случай окружность), гиперболу или параболу. Все другие кривые в прямоугольной системе координат будут описываться уравнениями более высокого порядка.
Ниже приведены канонические уравнения кривых второго порядка с центром симметрии (в случае параболы – вершиной) в начале координат (случай А) и в точке С (x 0, y 0) (случай В).
А В
| Окружность | 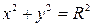
|
| |
| Эллипс | 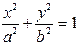
|
| |
| Гипербола | 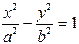
|
| |
| Парабола | 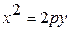
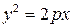
| 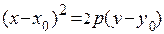 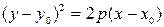
| |
Пример. Дано уравнение кривой второго порядка  . Определить тип кривой и сделать чертеж.
. Определить тип кривой и сделать чертеж.
Решение. Сравнивая с табличными данными находим, что это парабола, вершига которой находится в точке С (x 0, y 0). приводим уравнение параболы к виду 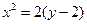 .
.
х0 = 0, у0 = 2, р = 1. Чертеж
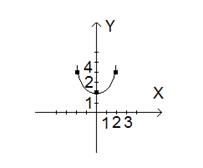
Рис. 22.
 2020-04-12
2020-04-12 127
127