Первісна фінкції та визначений інтеграл

14.

  n -вимірний векторний простір

Основні поняття

Означення. Сукупність упорядкованих систем з n дійсних чисел, для яких визначено дії додавання і множення на число, утворює n-вимірний векторний простір Vn.

Елементами заданого таким чином простору будуть впорядковані системи чисел, які називатимемо n - вимірними векторами і записуватимемо:. Числа ai, i = 1, 2, 3,..., n називаються компонентами вектора. Якщо розглянути ще один елемент простору Vn — вектор, то у просторі Vn можна виконувати такі дії.

Додавання двох векторів за правилом:

.

Множення вектора на число a, за правилом:

.

Два вектори і вважаються рівними, якщо виконуються рівності. Роль нуля відіграє. З означень дій додавання і множення вектора на число випливають властивості:

Означення. Вектор називається лінійною комбінацією векторів, якщо існують такі числа, що.

Система векторів називається лінійно залежною, якщо існують такі числа хоча б одне з яких відмінне від нуля, що виконується рівність

. (1.16)

Якщо рівність (1.16) можлива лише в разі, коли всі, то система векторів називається лінійно незалежною.

Постає запитання: а чи існують взагалі системи лінійно незалежних векторів? Розглянемо систему векторів в n -вимірному просторі Vn:

яку далі називатимемо одиничною системою векторів. Покажемо, що така система векторів лінійно незалежна. Для цього утворимо лінійну комбінацію:. Ліва частина цієї рівності є вектор. Звідси випливає, що всі.

 

 

15 Метод інтегрування частинами

Детальніше: Інтегрування частинами

Цей метод застосовується тоді, коли під інтегралом є добуток функцій, причому хоча би одна з них є трансцендентною (не степеневою).

Нехай u та v деякі функції х, тобто .

Розглянемо диференціал добутку цих функцій.

Інтегруючи обидві частини рівності, одержимо

Звідси, враховуючи властивість невизначеного інтеграла, маємо

Отже, одержали формулу

яку називають формулою інтегрування частинами.

Ця формула дозволяє знаходження інтеграла звести до зна­ходження інтеграла 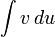. При вдалому обранні u то dv інтеграл може бути табличним або простішим ніж заданий інтеграл

Приклад. Знайти

Розв'язування. Нехай u = lnx, dv = dx. Тоді v = x

За формулою інтегрування частинами одержимо

 

№ 16. ВИЗНАЧНИКИ ДРУГОГО ТА ТРЕТЬОГО ПОРЯДКУ

 

Визначником другого порядку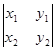

називається число =x₁y₂–y₁x₂

 

Визначником третього порядку  називається число =x₁y₂z₃+y₁z₂x₃+z₁x₂y₃–z₁y₂x₃–y₁x₂z₃– x₁z₂y₃

 

У визначнику можна визначити дві діагоналі. Головну діагональ визначника 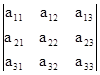утворюють елементи а₁₁, а₂₂, а₃₃. Побічну діагональ цього визначника складають елементи а₁₃, а₂₂, а₃₁.

Для обчислення визначника третього порядку існує правило трикутників. Визначник є сумою 6-и добутків, з яких три беруться зі знаком „+” і три – зі знаком „–”. Зі знаком „+” береться добуток елементів головної діагоналі і добуток елементів, які знаходяться у вершинах двох трикутників з основами, паралельними головній діагоналі

*	*	*
*	*	*	зі знаком „+”.
*	*	*

 

Зі знаком „–” береться добуток елементів побічної діагоналі і добутки елементів, що знаходяться у вершинах двох трикутників з основами, паралельними побічній діагоналі

*	*	*
*	*	*	зі знаком „–”
*	*	*

 

ПРИКЛАД:

1	5	-3
6	-8	2	=1∙(-8)∙1+5∙2∙9+6∙3∙(-3)–(-3)∙(-8)∙9- 6∙5∙1–3∙2∙1=
9	3	1	= -8+90–54–216–30–6=-224

 

Нехай дана система лінійних рівнянь другого порядку

α₁₁x+ α₁₂y=β₁

α₂₁x+ α₂₂y=β₂

Головним визначником системи називається визначник

	α11	α12
Δ=
	α21	α22	.

 

Якщо Δ≠0, для розв’язання системи існують формули Крамера. Домножимо перше рівняння системи на α₂₂, а друге рівняння - на α₁₂ і віднімемо з першого рівняння друге. При цьому одержимо рівняння, що є наслідком рівнянь системи, в цьому рівнянні залишається одна змінна х

(α₁₁α₂₂–α₁₂α₂₁)x=β₁α₂₂–β₂α₁₂

Згадуючи означення визначника другого порядку, це рівняння можна записати так:

 

	α11	α12		β1	α12
			x =
	α21	α22		β2	α22

Повернемось до початкової системи: домножимо перше рівняння на α₁₂, друге – на α₁₁ і віднімемо від другого рівняння перше. Одержимо рівняння, в якому лише одна змінна у.

(α₁₁α₂₂–α₁₂α₂₁)y= α₁₁β₂– α₂₁β₁

Або

	α11	α12		α11	β1
			y =
	α21	α22		α21	β2

Оскільки

	α11	α12
Δ=			≠0,	то з одержаних рівнянь знаходимо єдиний розв’язок
	α21	α22		початкової системи:

 

		β1		α12			α11	β1
x=		β2		α22	y =		α21	β2
	Δ						Δ

 

Позначаючи

 

	β1	α12		α11	β1
Δx=			Δy =			, остаточно отримаємо
	β2	α22		α21	β2

 

x= Δ_x/Δ, y= Δ_y/Δ.

Ці формули є формулами Крамера для системи лінійних рівнянь другого порядку.

Перейдемо до систем лінійних рівнянь третього порядку:

α₁₁x+α₁₂y+α₁₃z=β₁

α₂₁x+α₂₂y+α₂₃z=β₂

α₃₁x+α₂₃y+α₃₃z=β₃

Аналогічно системам другого порядку, головним визначником системи називається визначник

	α11	α23	α13
Δ=	α21	α22	α23
	α31	α32	α33

 

Покажемо, що при Δ≠0 для розв’язування системи третього порядку також існують формули Крамера.

Домножимо перше рівняння системи на число (α₂₂α₃₃ – α₂₃α₃₂), друге рівняння домножимо на (α₁₃α₃₂ – α₁₂α₃₃), третє рівняння – на (α₁₂α₂₃ – α₁₃α₃₃) і всі рівняння додамо. При цьому одержимо рівняння, що є наслідком системи і містить лише одну змінну х.

α₁₂α₂₂α₃₃–α₁₁α₂₃α₃₂+α₂₁α₁₃α₃₂–α₂₁α₁₂α₃₃+α₃₁α₁₂α₂₃–α₃₁α₁₃α₂₂)х=

β₁α₂₂α₃₃–β₁α₂₃α₃₂+β₂α₁₃α₃₂–β₂α₁₂α₃₃+β₃α₁₂α₂₃–β₃α₁₃α₂₂

Згадуючи означення визначника третього порядку, перепишемо рівняння у вигляді

 

	α11	α12	α13		β1	α12	α13
	α21	α22	α23	x=	β2	α22	α23
	α31	α32	α33		β3	α32	α33

Покладемо

 

	β1	α23	α13
Δx=	β2	α22	α23	і при Δ≠0 одержуємо x= Δx/Δ.
	β3	α32	α33

 

Проводячи аналогічні міркування для змінних y і z одержимо y= Δ_y/Δ z=Δ_z/Δ, де

	α11	β1	α13		α11	α12	β1
Δy=	α21	β2	α23	Δz=	α21	α22	β2
	α31	β3	α33		α31	α32	β3

 

Таким чином, якщо головний визначник Δ системи лінійних рівнянь третього порядку не дорівнює 0, система має єдиний розв’язок, який можна знайти за формулами Крамера

x= Δ_x/Δ y= Δ_y/Δ z=Δ_z/Δ

Нехай дана система лінійних рівнянь n -го порядку

α₁₁x₁+α₁₂x₂+…+α₁₃x_n=β₁

α₂₁x₁+α₂₂x₂+…+α₂₃x_n=β₂

………………………

α₃₁x₁+α₂₃x₂+…+α₃₃x_n=β_n

Для розв’язування подібних систем також існують формули Кроамера. Для того, щоб записати ці формули, потрібно ввести поняття визначника n -го порядку.

 

№ 17. Формула Ньютона – Лейбніца

 

Безпосередньо за означенням інтеграли легко обчислювати лише для найпростіших функцій, таких, як y = k x, y = x² Для інших функцій, наприклад тригонометричних, обчислення границь сум ускладнюється.

Виникає запитання: чи не можна обчислювати інтеграли іншим способом? Такий спосіб був знайдений лише у ХVII ст. англійським вченим Ісааком Ньютоном (1643 – 1727) і німецьким математиком Готфрідом Лейбніцом (1646 – 1716). Строге доведення формули Ньютон – Лейбніца дають у курсі математичного аналізу. Ми лише проілюструємо правильність формули геометричним міркуванням.

Виберемо довільну точку x є [ a; b]і проведемо через неї пенпендикуляр хК до осі Ох. Площа фігури а А К х змінюється зі змінною х. Позначемо цю функцію через S (x) і покажемо, що існує її похідна причина, при чому S΄(x)=ƒ(x), де y=ƒ(x) – підінтегральна функція, графік якої обмежує криволінійну трапецію. Інакше кажучи, покажемо, що S (x) є первісною для ƒ(x).

Надамо змінній x приросту Δx, вважаючи (для спрощення міркування), що Δx > 0. Тоді й фенкція S (x) набуде приросту ΔS (x). У курсі математичного аналізу доводиться, що неперервна на відрізку[ a; b]функція y=ƒ(x)досягає на цьому найбільшого і найменшого значень. Оскільки підінтегральна функція y=ƒ(x) є неперервною на відрізку[x,x+Δx], то вона досягає на цьому відрізку найменшого і найбільшого значень. Отже,

m Δx < Δ S (x) < M Δx

Позначимо через F(x)будь-яку первісну для функції y=ƒ(x). За основною властивістю первісної будь-які первісні для однієї і тієї самої функції можуть відрізнятися лише сталим додатком C. Тому

S(x) = F(x)+ C. (1)

При x=a криволінійна трапеція вироджується у відрізок a A, тому S(x) = 0.

Підставивши у рівність (1) замість х число а, а замість S(x) число 0, одер-жимо C= - F(a). Після підстановки замість C у рівність (1) його значення маємо

S(x) = F(x)-F(a). (2)

Коли x=b, то площа криволінійної трапеції дорівнює числуS=S(b). Крім того, за цією умови рівність (2) матиме вигляд

S(b) = F(b)-F(a).

Раніше було встановлено, що площа криволінійної трапеції дорівнює

b

значенню ∫ ƒ(x) dx. Тому можна зробити висновок, що

a

b

∫ ƒ(x) dx = F(b)-F(a). (3)

Це і є формула Ньютона-Лейбніца, яка показує, що значення інтегралу на відрізку[a;b] дорівнює різниці значень первісної підінтегральної функції при x=b i x=a.

Різницю F(b)-F(a) позначають. Тому рівність (3) можна записати так:

(кв. од.)

 

18.

18) Матриці: що складається з чисел , називають матрицею, а числа - елементами цієї матриці, де i вказує номер рядка, а j – номер стовпця. Добуток кількості рядків на кількість стовпчиків називають розміром матриці.

Коротко матрицю позначають так:

де , .

Матрицю розміру позначають .

Def. Матрицю, у якої число рядків дорівнює числу стовпців, називають квадратною. В іншому випадку матрицю називають прямокутною.

Def. Якщо всі елементи матриці дорівнюють нулю, то матрицю називають нульовою.

Елементи утворюють головну діагональ квадратної матриці, а елементи – побічну діагональ.

Def. Квадратну матрицю називають трикутною, якщо всі елементи, що розташовані під (над) головною діагоналлю, дорівнюють нулю, а серед тих, що залишилися, є ненульові.

Def. Квадратну матрицю, всі елементи якої, крім діагональних, дорівнюють нулю, називають діагональною.

Def. Квадратну матрицю, всі елементи головної діагоналі якої дорівнюють одиниці, а всі інші – нулю, називають одиничною і позначають

Def. Матрицю називають транспонованою до матриці , якщо рядки матриці є стовпцями матриці , а стовпці – рядками матриці .

Def. Матрицю, яка містить один стовпець, чи один рядок, називають вектор-стовпцем чи вектор-рядком відповідно. Наприклад,

 

Будь-якій квадратній матриці можна поставити у відповідність визначник (або ):

Def. Квадратну матрицю , визначник якої не дорівнює нулю, називають невиродженою.

Якщо , то матрицю називають відродженою.

N.B. Прямокутна матриця, яка не є квадратною, визначника не має.

 

19) Властивості визначеного інтеграла

Властивість 1. Постійний множник можна виносити за знак визначеного інтегралу: якщо , то  Властивість 2. Визначений інтеграл від алгебраїчної суми декількох функцій рівний алгебраїчній сумі інтегралів від доданків

Властивість 3. Якщо на відрізку де , функції і 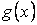задовольняють умові , то Властивість 4. Якщо і - найменше і найбільше значення функції на відрізку і , то  Властивість 5 (теорема про середнє). Якщо функція неперервна на відрізку , то на цьому відрізку знайдеться така точка 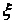, що справедлива рівність Властивість 6. Для будь-яких чисел справедлива рівність

первісна фінкції та визначений інтеграл.

Функція зветься первісною функції на деякому інтервалі дійсних чисел, якщо — похідна функції на цьому інтервалі, тобто в усіх внутрішніх точках інтервалу виконується рівність

Можна довести, що у будь-якої неперервної на інтервалі функції існує первісна, яка також є неперервною функцією на цьому інтервалі.

Якщо — будь-яка первісна функція то , де C - довільна стала, — також первісна цієї функції і "невизначений інтеграл функції " посилається до множини яка складається з усіх первісних функції де — довільнаконстанта.

      Визначений інтеграл — в математичному аналізі це інтеграл функції з вказаною областю інтегрування. Визначений інтеграл є неперервнимфункціоналом, лінійним по підінтегральним функціям і адитивним по області інтегрування. У найпростішому випадку область інтегрування — цевідрізок числової осі. Геометричний смисл цього визначеного інтеграла — це площа криволінійної фігури, обмеженої віссю абсцис, двома вертикалями на краях відрізка і кривою графіка функції.