Обчислення наближених значень деяких елементарних функцій

Нехай потрібно обчислити значення функції f(x) при х = х ₁ із заданою точністю .

Якщо функцію f(x) в інтервалі (-R; R) можна розкласти у степеневий ряд і , то точне значення f(x ₁) дорівнює сумі ряду при х = х ₁, тобто 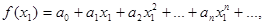а наближене - частковій сумі  тобто .

23.Обернена матриця, її побудова.

Якщо для квадратної матриці A існує така матриця X, що AX = XA = E (одинична матриця), то матрицю X називають оберненою матрицею до матриці A і позначають A ^-1.

Обернена матриця для кожної матриці єдина.

Матриця, детермінант якої дорівнює нулю, називається особливою (виродженою). В іншому випадку, матриця називається неособливою (невиродженою).

Щоб матриця мала обернену, необхідно і достатньо, щоб вона була неособливою.

Якщо detA =0, то

A −1=1 detA = } =1 detAA

, де Aij - алгебраїчні доповнення. Матрицю A називають приєднанною до матриці A.

24. Система n-лінійних рівнянь з n невідомими.

У загальному випадку система m лінійних рівнянь з n невідомими x 1, x 2…., xn має слідуючий вигляд:

a 11 x 1 + a 12 x 2 + … + a 1 nxn = b 1

a 21 x 1 + a 22 x 2 + … + a 2 nxn= b 2

am 1 x 1 + am 2 x 2+…+ amnxn = bm

Числа aij називають коефіцієнтами системи, а числа bi -- вільними членам и системи.

Розв'язком системи лінійних рівнянь називається упорядкована сукупність чисел a1, а2…а n (тобто, вектор), яка при підстановці замість невідомих перетворює кожне рівняння системи в тотожність.

Система лінійних рівнянь, яка має хоч один розв'язок, називається сумісною. Якщо система не має розв'язків, то вона називається несумісною.

Якщо сумісна система має лише один розв'язок, то її називають визначеною; в іншому випадку сумісну систему називають невизначеною.

Дві системи називаються рівносильними або еквівалентними, якщо вони мають одну і ту ж множину розв'язків.

Матрицю коефіцієнтів системи лінійних рівнянь називають основною матрицею або, просто, матрицею системи.

Систему лінійних рівнянь перепишемо у вигляді:

1)матричний спосіб

)

()

)

А^-1А*х=А^-1*В

Х=А^-1*В

2)Метод Крамера

∆₁=

∆₂=

3)метод гаусса

Спочатку зведемо розширену матрицю системи до східчастого виду. Нехай у матриці східчастого виду r ненульових рядків. Якщо в останньому ненульовому рядку всі елементи дорівнюють нулю, крім елемента з стовпця вільних членів, то система несумісна. Інакше, нехай перші ненульові коефіцієнти ненульових рядків матриці східчастого виду розташовані в стовпцях з номерами k 1…. kr. Тоді невідомі xk 1…. xkr називатимемо головними, а усі інші - вільними. Очевидно, кількість вільних невідомих дорівнює n − r. З матриці східчастого виду одержимо систему r рівняннь з n невідомими. Дістанемо вирази головних невўіомих через вільні. Ці вирази називаються загальним розв'язком системи.

25.Диференціал функції.Правила обчислення диференціалів.

Поняття диференціала тісно пов'язане з поняттям похідної, і е одним з найважливіших в математиці. Диференціал наближено до­рівнює приросту функції і пропорційний приросту аргументу. Вна­слідок цього диференціал широко застосовується при дослідженні різ­номанітних процесів і явищ. Будь-який процес протягом достатньо малого проміжку часу змінюється майже рівномірно, тому дійсний приріст величини, що характеризує процес, можна замінити дифе­ренціалом цієї величини на даному проміжку часу. Таку заміну на­зивають лінеаризацією процесу.

Термін «диференціал» (від латинського слова differentia — різни­ця) ввів у математику Лейбніц.

1. Означення, геометричний та механічний зміст диференціала

Нехай функція у = f (х) диференційовна в точці х [а; b], тобто в цій точці має похідну

Тоді з властивості 1o

при х 0,

звідки

(1)

Перший з доданків лінійний відносно х і при х 0 та f' (х) 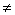0 є нескінченно малою одного порядку з х, тому що (гл. 4, п. 4.3):

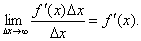
Другий доданок — нескінченно мала вищого порядку, ніж х, тому що

Цей доданок не є лінійним відносно х, тобто містить х в степені, вищому від одиниці. Таким чином, перший доданок у формулі (1) є головною частиною приросту функції, лінійною відносно приросту аргументу.

Диференціалом dy функції у = f (х) в точці х називається головна, лінійна відносно х, частина приросту функції f(х) в цій точці:

dy = f' (х) х. (2)

Диференціал dy називають також диференціалом першого порядку. Якщо у = х, то у' = х' = 1, тому dy = dx = х, тобто диферен­ціал dx незалежної змінної х збігається з її приростом х. Тому формулу (2) можна записати так:

dy = f'(x)dx. (3)

Формула (4) дає змогу розглядати похідну як відношення диферен­ціала функції до диференціала незалежної змінної.

Зауважимо, що коли в точці х0 похідна f' (х0) = 0, то перши й доданок у формулі (1) дорівнює нулеві і вже не є головною части­ною приросту . Але і в цьому випадку диференціал dy знаходять за формулою (4).

Геометричний зміст диференціала зрозумілий з рис. 5.18. Маємо

PN = y, QN = MNtg = хf'(x) = f'(x)dx = dy.

Отже, диференціал функції f (х) при заданих значеннях х і х до­рівнює приросту ординати дотичної до кривої у = f (х) в точці х. Приріст функції y при цьому дорівнює приросту ординати кривої. Таким чином, заміна приросту функції на її диференціал геометрично означає заміну ординати АР кривої ординатою дотичної AQ. Зрозумі­ло, що така заміна доцільна лише для достатньо малих значень х.

З'ясуємо механічний зміст диферен­ціала. Нехай матеріальна точка руха­ється за відомим законом

S = f(t), де f(t) — диференційовна на деякому про­міжку функція. Тоді диференціал цієї функції dS = f'(t) при фіксованих значеннях t і — це той шлях, який пройшла б матеріальна точка за час , якби вона рухалась прямолінійно і рів­номірно із сталою швидкістю . Зрозуміло, що фактичний шлях S у випадку нерівномірного руху на від­міну від диференціала dS не є лінійною функцією часу і тому відрізняється від шляху dS. Проте якщо час достатньо малий, то швидкість руху не встигає суттєво змінитись, і тому рух точки на проміжку часу від t до t + є майже рівномірним.

Поняття диференціала можна проілюструвати і на інших прикла­дах, які розглянуто в п. 1.1. У кожному з них поняття диференціала набуває конкретного фізичного змісту.

2. Властивості диференціала. Інваріантність форми диференціала

Оскільки диференціал функції дoрівнює добутку її похідної на диференціал незалежної змінної, то властивості диференціала можна легко дістати із відповідних властивостей похідної. Якщо, наприклад, и і v — диференційовні функції від х, С — стала, то маємо такі правила знаходження диференціалів:

d (u ± ) = du ± d ;

Доведемо, наприклад, четверту формулу. За означенням диферен­ціала маємо

d (uv) = (uv)'xdx = (u'v + uv') dx — = vu'dx + uv'dx = vdu + udv.

Таблиця диференціалів

26

26.Метод Крамера — спосіб розв'язання квадратних систем лінійних алгебраїчних рівнянь із ненульовим визначником основної матриці (при цьому для таких рівнянь розв'язок існує і є єдиним). Метод було створено Габріелем Крамером у 1750 році. Для системи лінійних рівнянь з невідомими (над довільним полем)з визначником матриці системи , що не рівний нулю, розв'язок записується у такому вигляді:1-й стовпчик матриці системи замінюється стовпчиком вільних членів).

1.[A]=0 чи не =0,

Система лінійних рівнянь:     2.- дельта [А]

Визначники:

Розв'язок: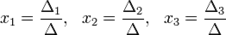

Приклад:

Визначники:

 

27. Правила диференціювання

 

28 Зміст похідної

Похідна́ — основне поняття диференційного числення, що характеризує швидкість зміни функції. Визначається як границя відношення приросту функції до приросту її аргументу коли приріст аргументу прямує до нуля (якщо така границя існує). Функцію, що має скінченну похідну, називають диференційовною

Похідна функції має такий фізичний зміст: похідна функції в заданій точці – швидкість зміни функції в заданій точці.

Похідна функції має такий геометричний зміст: похідна функції в заданій точці є кутовим коефіцієнтом дотичної до графіка функції в цій точці, тобто дорівнює тангенсу кута нахилу дотичної до графіка функції в заданій точці.

 

29 Означення похідної

Похідною функції f(x) у точці х₀ називається границя (якщо вона існує) відношення приросту функції у точці х₀ до приросту аргументу Δх, якщо приріст аргументу прямує до нуля і позначається f'(x₀).

Дія знаходження похідної функції називається диференціюванням.

 

30 Метод потенціалів

Транспортна задача є задачею лінійного програмування, яку можна розв’язати симплекс-методом. Але специфічна структура транспортної задачі дає змогу використовувати для її розв’я­зування ефективніший метод, який повторює, по суті, кроки симплекс-алгоритму. Таким є метод потенціалів.
Алгоритм методу потенціалів складається з таких етапів.
1. Визначення типу транспортної задачі (відкрита чи закрита).
2. Побудова першого опорного плану транспортної задачі.
3. Перевірка плану транспортної задачі на оптимальність.
4. Якщо умова оптимальності виконується, то маємо оптимальний розв’язок транспортної задачі. Якщо ж умова оптимальності не виконується, необхідно перейти до наступного опорного плану.
5. Новий план знову перевіряють на оптимальність, тобто повторюють дії п. 3, і т. д.

Пит.36

Функцію можна задавати:

· аналітично (коли функція задається формулами);

· табличним способом – при цьому в таблиці надаються значення змінної х і відповідні їм значення у;

· описовим способом – коли функція задається словесним описом;

· графічно – коли функція задається її графіком.

37

Елементарні функції — клас функцій, що містить в собі степеневі функції, многочлени, показникові функції, логарифмічні функції, тригонометричні функції, зворотні тригонометричні функції, а також функції, що отримуються із перелічених вище за допомогою чотирьох арифметичних операцій (додавання, віднімання, множення, ділення) та композиції, застосованих скінченну кількість разів. Наприклад, раціональні функції є відношеннями многочленів, тому вони належать до елементарних функцій. Так само, неважко переконатися, що до елементарних функцій належать гіперболічні та зворотні гіперболічні функції.

Показнико́ва фу́нкція — функція виду , де — стале число (додатне, але не дорівнює одиниці). Показникова функція може бути визначена двома еквівалентними способами. Через ряд Тейлора:

або через границю:

Логарифмічна функція ставить у відповідність кожному значенню змінної її логарифм за наперед обраною основою .

Тригонометри́чні фу́нкції — це функції кута, особливо корисні при дослідженні та моделюванні періодичних подій. Вони можуть бути визначені як відношення двох сторін трикутника що містить кут, або як відношення координат точок по колу, або, більш загально, як нескінченні ряди, або як розв'язок диференційного рівняння. ЧОТИРИ базових тригонометричних функцій.

синус (sin) косинус (cos) тангенс (tg = sin / cos) котангенс (ctg = cos / sin)