Интервальные оценки для генеральной дисперсии и среднего квадратического отклонения

Пусть из генеральной совокупности X, распределённой по нормальному закону N(μ;σ), взята случайная выборка объёмом n и вычислена выборочная дисперсия S². Требуется определить с надёжностью γ интервальные оценки для генеральной дисперсии σ² и среднего квадратического отклонения σ при малом объёме выборки (n ≤ 30).

Построение доверительного интервала для генеральной дисперсии основывается на том, что случайная величина имеет распределение Пирсона (χ²) с k = n – 1 степенями свободы.

Для выбранной доверительной вероятности γ = 1 – α, учитывая, что имеет распределение χ² с k = n – 1 степенями свободы, можно записать:

 Далее по таблице χ²-распределения нужно выбрать такие два значения и , чтобы площадь, заключённая под дифференциальной функцией распределения χ² между 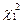и , была равна γ = 1 – α.

Обычно 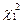и выбирают так, чтобы

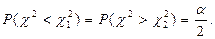
Тогда имеем

Так как таблица χ²-распределения содержит лишь , то для вычисления запишем следующее тождество:

Осуществив подстановку значений, получим:

Отсюда

Эта формула используется при решении обратной задачи – нахождении доверительной вероятности по заданному доверительному интервалу генеральной дисперсии.

Причём

Преобразовав двойное неравенство окончательно получим:

 Это и есть доверительный интервал для генеральной дисперсии, когда неизвестно значение генеральной средней и по выборке объёмом n вычисляется выборочная дисперсия S².

Ширина доверительного интервала для генеральной дисперсии равна:

Доверительный интервал для генерального среднего квадратического отклонения σ при n ≤ 30 равен:

При достаточно больших объёмах выборки (n > 30) значения и определяют по формулам:

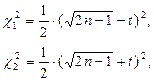
а доверительный интервал для генерального среднего квадратического отклонения определяется по формуле:

где t – нормированное значение нормальной случайной величины, соответствующее заданной надёжности γ и определяемое по таблице функции Лапласа Ф(t).

Пример 3. По результатам контроля n = 9 деталей вычислено выборочное среднее квадратическое отклонение S = 5 мм. В предположении, что ошибка изготовления деталей распределена нормально, определить с надёжностью γ = 0,95 доверительный интервал для параметра σ.

Решение. Так как n < 30, то используется χ²-распределение:

По таблице χ²-распределения для числа степеней свободы k = n – 1 = 8 и найденных вероятностей 0,975 и 0,025 определяем, что 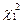= 2,180 и         = 17,535.

Вычисляем и .

Доверительный интервал для среднего квадратического отклонения равен:

и окончательно получаем: 3,6 ≤ σ ≤ 10,2 (мм).