y''+py'+qy=f(x),где p и q – const
f(x)  неоднородное,
неоднородное,  – общее решение неоднородного
– общее решение неоднородного
f(x)=0 однородное 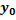 – общее решение соответствующего однородного
– общее решение соответствующего однородного
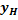 =
= 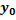 +
+  где
где  – любое решение неоднородного уравнения
– любое решение неоднородного уравнения
Общее решение однородного уравнения
y''+py'+qy=0
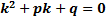 – характеристическое уравнение
– характеристическое уравнение
1) 
2) 
3)k= 
Примеры. Найти общее решение линейного однородного уравнения
1) 
Шаг 1: составляем характеристическое уравнение:
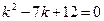
Шаг 2: находим корни характеристического уравнения:
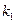 =3,
=3, 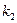 =4. Здесь
=4. Здесь 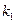
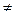
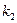 , случай 1,
, случай 1,
Шаг 3: выписываем решение, формула (5).
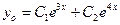
2) 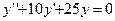
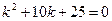
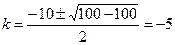
Здесь 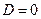 ,
, 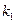 =
= 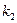 = -5, случай 2,
= -5, случай 2,  находим по формуле (6)
находим по формуле (6)

3) 


Здесь случай 3, 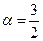 ,
, 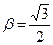 , для
, для  выбираем формулу (7)
выбираем формулу (7)

4) 
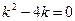
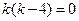
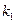 =0,
=0, 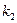 =4,
=4, 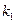
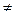
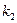 , случай 1), формула (5).
, случай 1), формула (5).


5) 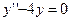
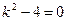
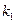 =2,
=2, 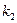 = -2,
= -2, 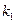
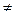
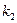 , случай 1), формула (5).
, случай 1), формула (5).
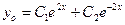
6) 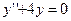
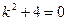
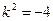 ,
, 
Здесь случай 3,  ,
,  , формула (7)
, формула (7)
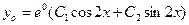

Метод неопределенных коэффициентов определения 
1) f(x)= 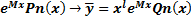
l= 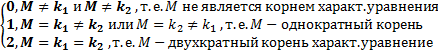
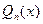 – многочлен той же степени, что и
– многочлен той же степени, что и  , но с неопределенными коэффициентами.
, но с неопределенными коэффициентами.
2) f(x)= 
l= 
Замечание 1.  – частный случай
– частный случай  первого типа при
первого типа при 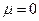 .
.
 (А – постоянная величина) – частный случай
(А – постоянная величина) – частный случай  первого типа, здесь
первого типа, здесь  =А – многочлен нулевой степени.
=А – многочлен нулевой степени.
Замечание 2. Как записывается 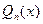 .
.
Обозначим неопределенные коэффициенты А, В, С, … Тогда 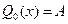 ,
, 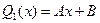 ,
,
 ,
,  ,…
,…
7) а) Найти общее решение уравнения y''-2y'= 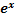 (
(  -x-3)
-x-3)
1.Находим общее решение соответствующего однородного уравнения y''-2y'=0.
 -2k=0 k(k-2)=0
-2k=0 k(k-2)=0  =0
=0  =2
=2 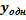 =
= 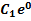 + C2e2x=
+ C2e2x= 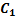 + C2e2x
+ C2e2x
2. Анализируем правую часть уравнения и выписываем  с неопределенными коэффициентами в соответствии с формулами (8)
с неопределенными коэффициентами в соответствии с формулами (8)
f(x)= 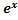 (
(  -x-3),
-x-3), 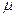 = 1
= 1  .
.  -x-3=
-x-3=  (x)
(x) 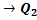 (x)
(x)
 =
=  (x)=
(x)= 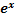 (A
(A  +Bx+C).
+Bx+C).
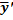 =
= 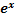 (A
(A  +Bx+C)+
+Bx+C)+ 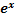 (2Ax+B)=
(2Ax+B)= 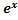 (A
(A  +Bx+C+2Ax+B)
+Bx+C+2Ax+B)
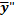 =
= 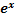 (A
(A  +Bx+C+2Ax+B)+
+Bx+C+2Ax+B)+ 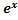 (2Ax+B+2A)=
(2Ax+B+2A)= 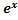 (A
(A  +Bx+C+4Ax+2B+2A)
+Bx+C+4Ax+2B+2A)
Подставляем 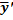 и
и 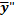 в левую часть исходного уравнения, общий множитель ex выносим за скобки
в левую часть исходного уравнения, общий множитель ex выносим за скобки
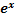 (A
(A  +Bx+C+4Ax+2B+2A-2A
+Bx+C+4Ax+2B+2A-2A  -2Bx-2C-4Ax-2B)=
-2Bx-2C-4Ax-2B)= 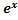 (
(  -x-3)
-x-3)
Многочлен в левой части распишем по степеням x
 (A-2A)+x(B+4A-2B-4A)+C+2B+2A-2C-2B=
(A-2A)+x(B+4A-2B-4A)+C+2B+2A-2C-2B=  -x-3
-x-3
Два многочлена могут быть равны тогда и только тогда, когда у них равны коэффициенты при одинаковых степенях x. Приравнивая коэффициенты при одинаковых степенях x в правой и левойчасти, получаем систему линейных уравнений для определения A, B и C
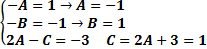
Итак,  =
= 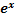 (-
(-  +x+1)
+x+1)
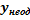 =
= 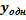 +
+  =
= 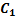 +C2e2x +
+C2e2x + 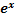 (-
(-  +x+1).
+x+1).
б)Найти частное решение исходного уравнения yчастн, удовлетворяющее заданным начальным условиям
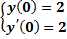
y(0)=2 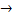
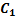 +
+  +1=2
+1=2  +
+  =1
=1
 =2
=2  +
+ 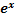 (-
(-  +x+1)+
+x+1)+ 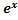 (-2x+1)
(-2x+1)
y'(0)=2 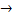 2
2  +1+1=2
+1+1=2 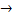 2
2  =0
=0  =0
=0 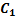 =1;
=1; 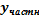 =1+
=1+ 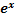 (-
(-  +x+1)
+x+1)
Примеры.
1)Найти общее решение уравнения y''- 4y'+4y=3 e2x
1.Находим общее решение соответствующего однородного уравнения y''-4y'+4y=0.
 -4k+4= 0
-4k+4= 0  =
=  =2
=2 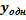 =(
=( 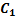 x+ C2) e2x
x+ C2) e2x
2. Анализируем правую часть уравнения и выписываем  с неопределенными коэффициентами в соответствии с формулами (8)
с неопределенными коэффициентами в соответствии с формулами (8)
f(x)=3 e2x , 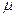 =2=k1=k2
=2=k1=k2  l=2 3=P0(x)
l=2 3=P0(x) 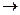 Q0(x)=A
Q0(x)=A
 = Ax2e2x
= Ax2e2x 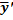 = 2 e2x A
= 2 e2x A  +2Ax e2x = e2x (2A
+2Ax e2x = e2x (2A  +2Ax)
+2Ax)
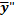 =2 e2x (2A
=2 e2x (2A  + 2Ax)+ e2x (4Ax+2A)= e2x (4A
+ 2Ax)+ e2x (4Ax+2A)= e2x (4A  +8Ax+2A)
+8Ax+2A)
Подставляем 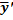 и
и 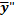 в левую часть исходного уравнения, общий множитель e2x выносим за скобки
в левую часть исходного уравнения, общий множитель e2x выносим за скобки
e2x (4A  +8Ax+2A-8A
+8Ax+2A-8A  -8Ax+ 4Ax2)= 3e2x
-8Ax+ 4Ax2)= 3e2x
Многочлен в левой части распишем по степеням x
 (4A-8A+4A)+x(8A-8A)+2A=3
(4A-8A+4A)+x(8A-8A)+2A=3 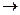 2A=3, A=1.5
2A=3, A=1.5
Итак,  =1.5x2e2x;
=1.5x2e2x;
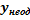 =
= 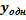 +
+  =(
=( 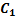 x+C2) e2x +1.5x2e2x
x+C2) e2x +1.5x2e2x
2)Найти общее решение уравнения y''- 4y'+8y=sin2x
1.Находим общее решение соответствующего однородного уравнения y''-4y'+8y=0.
 -4k+8=0 k=
-4k+8=0 k= 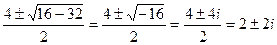 ,
, 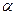 =2,
=2,  ,
, 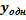 =(
=( 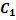 cos2x+ C2sin2x) e2x
cos2x+ C2sin2x) e2x
2. Анализируем правую часть уравнения и выписываем  с неопределенными коэффициентами в соответствии с формулами (9)
с неопределенными коэффициентами в соответствии с формулами (9)
f(x)=sin 2x, 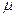 =0
=0  =2,
=2, 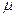 +i
+i  =2i
=2i  l=0
l=0
 = x0(Acos2x+Bsin2x)= Acos2x+Bsin2x,
= x0(Acos2x+Bsin2x)= Acos2x+Bsin2x,
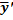 = -2Asin2x+2Bcos2x,
= -2Asin2x+2Bcos2x, 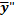 = -4Acos2x-4Bsin2x,
= -4Acos2x-4Bsin2x,
Подставляем 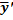 и
и 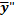 в левую часть исходного уравнения
в левую часть исходного уравнения
-4Acos2x-4Bsin2x+8Asin2x-8Bcos2x+8Acos2x+8Bsin2x=sin2x
Cos2x(4A-8B)+sin2x(8A+4B)=sin2x
Равенства вида Mcos 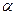 x+Nsin
x+Nsin 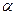 x= Pcos
x= Pcos 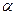 x+Qsin
x+Qsin 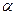 x имеют место тогда и только тогда, когда коэффициенты при cos
x имеют место тогда и только тогда, когда коэффициенты при cos 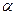 x и sin
x и sin 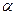 x слева и справа соответственно равны, то есть
x слева и справа соответственно равны, то есть
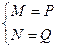
Таким образом, коэффициенты A и B – решения системы уравнений

A=0.1, B=0.05
 =
= 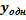 +
+  =(
=( 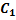 cos2x+ C2sin2x) e2x+0.1cos2x+0.05sin2x
cos2x+ C2sin2x) e2x+0.1cos2x+0.05sin2x
3)y''-2y'= 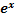 (
( 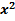 -x-3)
-x-3) 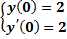
y''-2y'=0 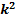 -2k=0 k(k-2)=0
-2k=0 k(k-2)=0  =0
=0 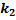 =2
=2 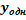 =
= 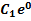 +
+  =
= 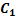 +
+ 
f(x)= 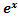 (
( 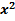 -x-3) M=1
-x-3) M=1 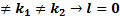
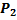 (x)
(x) 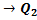 (x)
(x)
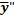 =
=  (x)=
(x)= 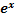 (A
(A 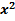 +Bx+C)
+Bx+C)
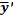 =
= 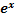 (A
(A 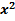 +Bx+C)+
+Bx+C)+ 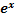 (2Ax+B)=
(2Ax+B)= 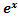 (A
(A 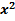 +Bx+C+2Ax+B)
+Bx+C+2Ax+B)
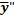 =
= 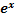 (A
(A 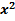 +Bx+C+2Ax+B)+
+Bx+C+2Ax+B)+ 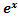 (2Ax+B+2A)=
(2Ax+B+2A)= 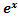 (A
(A 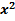 +Bx+C+4Ax+2B+2A)
+Bx+C+4Ax+2B+2A)
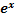 (A
(A 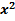 +Bx+C+4Ax+2B+2A-2A
+Bx+C+4Ax+2B+2A-2A 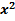 -2Bx-2C-4Ax-2B)=
-2Bx-2C-4Ax-2B)= 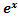 (
( 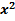 -x-3)
-x-3)
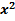 (A-2A)+x(B+4A-2B-4A)+C+2B+2A-2C-2B=
(A-2A)+x(B+4A-2B-4A)+C+2B+2A-2C-2B= 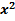 -x-3
-x-3
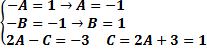
 =
= 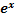 (-
(- 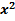 +x+1)
+x+1)  =
= 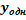 +
+  =
= 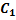 +
+  +
+ 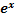 (-
(- 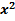 +x+1)
+x+1)
y(0)=2 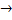 =
= 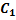 +
+ 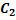 +1
+1 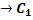 +
+ 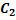 =1
=1
 =2
=2 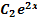 +
+ 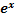 (-
(- 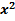 +x+1)+
+x+1)+ 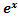 (-2x+1)
(-2x+1)
y’(0)=2 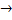 2=2
2=2 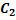 +1+1
+1+1 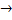 2
2 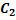 =0
=0  =0
=0 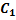 =1
=1 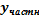 =1+
=1+ 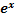 (-
(- 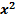 +x+1)
+x+1)
4)y”+9y=37 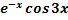
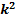 +9=0
+9=0 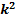 =-9
=-9 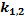 =
= 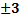
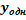 =
= 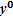 (
( 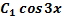 +
+  )=
)= 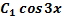 +
+ 
f(x)= 37 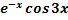 M=-1 V=3 M+iV=-1+3i
M=-1 V=3 M+iV=-1+3i 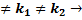 l=0
l=0
 =
= 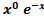 (Acos3x+Bsin3x)=
(Acos3x+Bsin3x)= 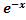 (Acos3x+Bsin3x)=
(Acos3x+Bsin3x)= 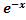 (Acos3x+Bsin3x)
(Acos3x+Bsin3x)
 ’=-
’=-  (-Acos3x-Bsin3x-3Asin3x+3Bcos3x)+
(-Acos3x-Bsin3x-3Asin3x+3Bcos3x)+ 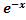 (3Asin3x-3Bcos3x-9Acos3x-9Bsin3x)=-9Acos3x-9Bsin3x)
(3Asin3x-3Bcos3x-9Acos3x-9Bsin3x)=-9Acos3x-9Bsin3x)
 (-8Acos3x-8Bsin3x+6Asin3x-6Bcos3x+9Acos3x+9Bsin3x)= 37
(-8Acos3x-8Bsin3x+6Asin3x-6Bcos3x+9Acos3x+9Bsin3x)= 37 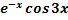
cos3x(A-6B)+sin3x(B+6A)= 37 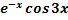
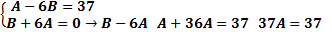 A=1 B=-6
A=1 B=-6
 =-
=-  (cos3x-6sin3x)
(cos3x-6sin3x)
 =
=  +
+  =
= 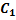 cos3x+
cos3x+ 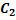 sin3x+
sin3x+  (cos3x-6sin3x)
(cos3x-6sin3x)
5) Найти общее решение уравнения
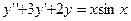
Характеристическое уравнение имеет вид 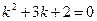 , его корни
, его корни  = -1,
= -1, 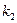 = -2. Здесь
= -2. Здесь 
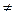
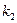 , случай 1, решение однородного уравнения выписывается по формуле (5):
, случай 1, решение однородного уравнения выписывается по формуле (5): 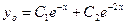
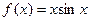 – правая часть третьего типа,
– правая часть третьего типа,  определяется формулой (10).
определяется формулой (10).
Здесь  и
и 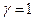 ,
, 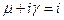 не является корнем характеристического уравнения
не является корнем характеристического уравнения 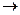
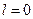 .
.
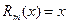 – многочлен первой степени (m=1).
– многочлен первой степени (m=1).
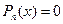 – многочлен нулевой степени (n=1).
– многочлен нулевой степени (n=1).
В формуле (10) 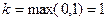
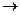


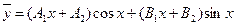 ,
,
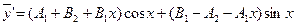 ,
,
 .
.
Подставляя эти выражения в исходное уравнение, будем иметь
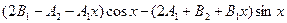 +
+  +
+
+ 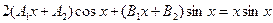
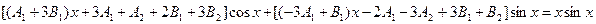
Отсюда получаем систему линейных уравнений относительно 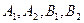
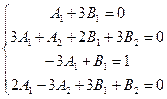
Решая эту систему, найдем  ,
, 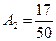 ,
,  ,
,  и частное решение
и частное решение 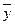 запишется так:
запишется так:
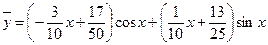 .
.
Общее решение данного уравнения
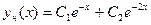 +
+ 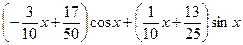 .
.
6) Проинтегрировать уравнение 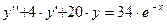 .
.
Найдем сначала общее решение соответствующего однородного уравнения
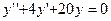 .
.
Характеристическое уравнение  имеет корни
имеет корни
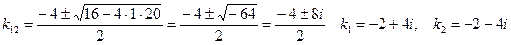
Следовательно, общее решение однородного уравнения определяется формулой
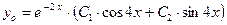 .
.
Переходим к отысканию частного решения исходного уравнения.
Так как в данном случае 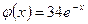 (т.е. имеет вид
(т.е. имеет вид 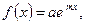 где
где  ,
, 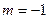 ) и
) и 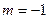 не является корнем характеристического уравнения, то частное решение ищем в виде
не является корнем характеристического уравнения, то частное решение ищем в виде
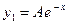 .
.
Найдя производные этой функции
 и
и 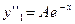 ,
,
и подставляя выражения для 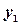 ,
, 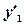
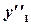 в исходное уравнение, получаем
в исходное уравнение, получаем
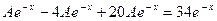 .
.
Так как 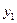 - решение уравнения, то последнее равенство выполняется для всех
- решение уравнения, то последнее равенство выполняется для всех  , т.е. является тождеством:
, т.е. является тождеством:
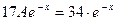
откуда 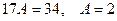 . Следовательно, частное решение имеет вид
. Следовательно, частное решение имеет вид
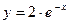 .
.
Соответственно, общее решение
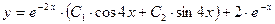 .
.
7) Решить уравнение 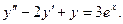
Составим характеристическое уравнение для соответствующего линейного однородного дифференциального уравнения:
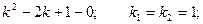
Общее решение однородного уравнения: 
Теперь найдем частное решение неоднородного уравнения в виде:
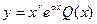
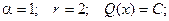
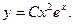
Воспользуемся методом неопределенных коэффициентов.
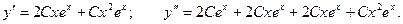
Подставляя в исходное уравнение, получаем:


Частное решение имеет вид: 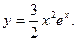
Общее решение линейного неоднородного уравнения: 
8) Решить уравнение 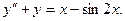
Правую часть дифференциального уравнения представим в виде суммы двух функций f1(x) + f2(x) = x + (- sin x).
Составим и решим характеристическое уравнение: 
1. Для функции f1 (x) решение ищем в виде  .
.
Получаем:  Т.е.
Т.е. 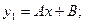

Итого: 
2. Для функции f2 (x) решение ищем в виде:  .
.
Анализируя функцию f2 (x), получаем: 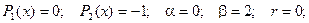
Таким образом, 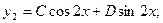

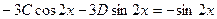
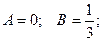
Итого: 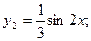
Т.е. искомое частное решение имеет вид: 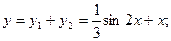
Общее решение неоднородного дифференциального уравнения:

 2020-04-12
2020-04-12 992
992






