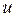Отыскание параметров выборочного уравнения линейной регрессии по сгруппированным данным

При большом числе опытов одно и то же значение x_i может встретиться 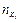раз, а одно и то же значение y_j соответственно раз. Одна и та же пара значений (x_i,y_j) может наблюдаться  раз. Поэтому наблюдаемые значения могут быть сгруппированы. Для этого подсчитывают частоты и результаты заносят в таблицу, которая обычно называется корреляционной. Примером корреляционной таблицы является таблица 12.1.

Таблица 12.1.

yj	xi
	10	20	30	40	nyj
3 5 7	4 2 -	7 1 2	3 6 -	5 5 3	19 13 5
nxi	6	10	9	13

На пересечении строк и столбцов указывается частота n_ij  для пары (x_i,y_j). Очевидно, что . В этом случае выборочное уравнение прямой линии регрессии Y на X имеет вид:

(12.1)

где  – условная средняя;  и  – выборочные средние признаков X и Y;  и  – выборочные средние квадратические отклонения; r_в – выборочный коэффициент корреляции, причем:

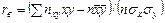
(12.2)

 

Выборочное уравнение прямой линии регрессии X на Y имеет вид:

(12.3)

Если данные наблюдений над признаками X и Y заданы в виде корреляционной таблицы с равноотстоящими вариантами, то целесообразно перейти к условным вариантам:

,          ,

где С₁ – «ложный нуль» вариант X (новое начало отсчета); в качестве ложного нуля выгодно принять варианту, которая расположена примерно в середине вариационного ряда (условимся принимать в качестве ложного нуля варианту, имеющую наибольшую частоту); h ₁ – шаг, т.е. разность между двумя соседними вариантами X; С ₂ – ложный нуль вариант Y; h ₂ – шаг вариант Y.

В этом случае выборочный коэффициент корреляции:

(12.4)

причем слагаемое  удобно вычислять, используя расчетную таблицу 12.3.

Величины , , ,  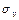могут быть найдены либо методом произведений (при большом числе данных), либо непосредственно по формулам:

, , ,

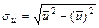1. Зная эти величины, можно определить входящие в уравнения регрессии (12.1) и (12.3) величины по формулам:

 

, , ,

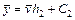Для оценки силы линейной корреляционной связи служит выборочный коэффициент корреляции r_в.

Для обоснованного суждения о наличии связи между количественными признаками следует проверить, значим ли выборочный коэффициент корреляции.

Пример 12.1. Найти выборочное уравнение прямой линии регрессии Y на X по данным, приведенным в корреляционной таблице 12.2.

Таблица 12.2

Y	X					ny
	20	25	30	35	40
16	4	6	-	-	-	10
26	-	8	10	-	-	18
36	-	-	32	3	9	44
46	-	-	4	12	6	22
56	-	-	-	1	5	6
nx	4	14	46	16	20	n = 100

Решение: Составим корреляционную таблицу 12.3 в условных вариантах, выбрав в качестве ложных нулей С ₁ = 30 и С ₂ = 36 (каждая из этих вариант расположена в середине соответствующего вариационного ряда).

Таблица 12.3

	-2	-1	0	1	2
-2	4	6	-	-	-	10
-1	-	8	10	-	-	18
0	-	-	32	3	9	44
1	-	-	4	12	6	22
2	-	-	-	1	5	6
	4	14	46	16	20	n = 100

Найдем 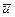 и :

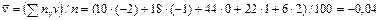
Найдем вспомогательные величины  и :

Найдем  и :

Найдем , для чего составим расчетную таблицу 12.4.

Таблица 12.4

	u
	-2			-1			0			1			2
-2			-8			-6	-			-			-			-14	28
	4			6
	-8			-12
-1	-					-8			0	-			-			-8	8
				8			10
				-8			-10
0	-			-					0			3			18	21	0
							32			3			9
							0			0			0
1	-			-					0			12			12	24	24
							4			12			6
							4			12			6
2	-			-			-					1			10	11	22
											1			5
										2			10
	-8			-20			-6			14			16
	16			20			0			14			32

 Суммируя числа последнего столбца таблицы 12.3, находим:

2. Для контроля вычислений находим сумму чисел последней строки:

3. Совпадение сумм свидетельствует о правильности вычислений.

Пояснения к составлению таблицы 3.

1. Произведение частоты  на варианту u, т.е. , записывают в правом верхнем углу клетки, содержащей значение частоты. Например, в правых верхних углах клеток первой строки записаны произведения: ; .

2. Складывают все числа, помещенные в правых верхних углах клеток одной строки, и их сумму помещают в клетку этой же строки «столбца U». Например, для первой строки .

4. Наконец, умножают варианту v на U и полученное произведение записывают в соответствующую клетку «столбца vU». Например, в первой строке таблицы , , следовательно, .

5. Сложив все числа «столбца vU», получают сумму , которая равна искомой сумме . Например, для таблицы 3, 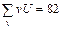, следовательно, искомая сумма .

Для контроля аналогичные вычисления производят по столбцам: произведения  записывают в левый нижний угол клетки, содержащей значение частоты; все числа, помещенные в левых нижних углах клеток одного столбца, складывают и их сумму помещают в «строку V»; наконец, умножают каждую варианту u на V и результат записывают в клетках последней строки.

Сложив все числа последней строки, получают сумму , которая также равна искомой сумме . Например, для таблицы 12.3, , следовательно, .

Найдем искомый выборочный коэффициент корреляции:

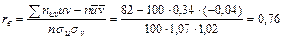
Найдем шаги h ₁ и h ₂ (разности между любыми двумя соседними вариантами): ;

Найдем 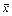 и 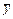, учитывая, что С ₁ = 30, С ₂ = 36:

Найдем 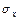 и :

;

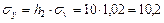
Подставив найденные величины в соотношение 12.1, получим искомое уравнение прямой линии регрессии Y на X:

,

или окончательно: