Интегральные уравнения электростатики проводников

     12.1. Интегральные уравнения первого рода. Электрический потенциал поля, которое возбужденно заряженным проводником, можно определить в любой точке пространства, если известна плотность зарядов на поверхности проводника S:

     Если задан потенциал проводника 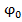, то, поместив точку наблюдения 1 на поверхность S, получаем интегральное уравнение первого рода относительно плотности заряда σ:

 

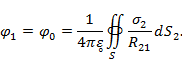
Ядро интеграла имеет интегрируемую особенность. Заменив интеграл конечной суммой, можно найти приближенное решение интегрального уравнения как решение системы линейных алгебраических уравнений.

     Если задан заряд проводника q, то в уравнении (24) можно произвольно задать постоянную 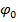 и, решив его, найти соответствующий заряд

.

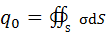Заряд и потенциал проводника пропорциональны

,

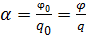где φ-потенциал проводника с зарядом q. Следовательно. φ=αq.

     Электрический потенциал в любой точке пространства и плотность заряда в любой точке на поверхности проводника пропорциональны его заряду. Поэтому плотность заряда на поверхности проводника с зарядом q во столько раз больше плотности заряда на поверхности того же проводника с зарядом 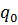, во сколько раз q больше, чем 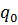, т.е. 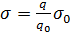, где 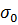- решение интегрального уравнения (24), соответствующее выбранному значению потенциала проводника  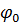и его заряду .

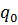     12.2. Интегральные уравнения второго рода. Если известна плотность электрического заряда σ на поверхности S заряженного проводника, то напряженность электрического поля в любой точке пространства можно определить методом интегрирования источников,

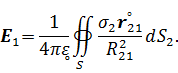
     На поверхности проводника напряженность имеет только нормальную составляющую, которая испытывает разрыв первого рода величиной 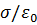. Если в окрестности точки наблюдения поверхность S является гладкой, то вектор напряженности можно разложить на две составляющих: на наружной стороне поверхности проводника

и на её внутренней стороне

.

 

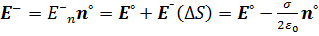Здесь использованы обозначения:

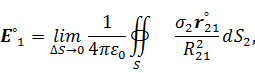
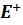 (ΔS)- напряженность поля, созданного заряженным элементом поверхности ΔS на его наружной стороне, 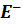(ΔS)- напряженность того же поля на внутренней стороне поверхности S (рис.22а.).

     Перейдем к скалярным уравнениям, умножив векторные уравнения почлено на 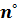 (единичную нормаль в точке наблюдения):

,

.

 

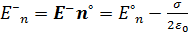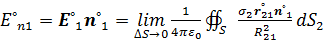Главное значение несобственного интеграла 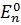 не изменяется при ΔS 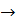0, потому, что на гладком элементе ΔS в окрестности точки наблюдения 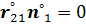и он не дает никакого вклада в интеграл (рис.22б).

      а) 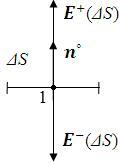                            б)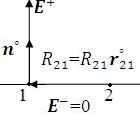          

Рис.22. Собственное поле заряженного элемента поверхности ΔS (а) и поле заряженного проводника в окрестности этого элемента (б).

     Подставим выражение (26) для 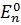 в правую часть равенства (25) и учтём, что внутри проводника электрического поля нет ( 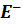=0). В результате получается интегральное уравнение второго рода относительно плотности заряда на поверхности проводника

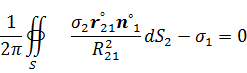
Точка наблюдения 1 находится на поверхности проводника S. Когда точка интегрирования 2 приближается к точке наблюдения 2 функция 1/ 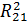 неограниченно возрастает. В последней формуле предполагается главное значение несобственного интеграла. В математической физике ядро этого интеграла принято записывать в виде

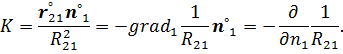
     Интегральное уравнение (27) является однородным, его решением σ(x,y,z) является собственная функция интегрального оператора с ядром K на поверхности S, соответствующая характеристическому числу 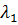=1/2π. Собственная функция определяется с точностью до коэффициента, поэтому решение интегрального уравнения следует нормировать условием

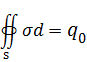
где q₀ - заряд проводника. При необходимости можно найти потенциал проводника φ₀ по формуле (24) и его потенциальный коэффициент α=φ₀/q₀. Зная величину α, можно подогнать заряд проводника и соответственно функцию σ к любому значению его потенциала.

     12.3. Дополнения к §12. Заряженный проводник во внешнем электрическом поле. Если рядом с проводником расположен точечный заряд 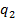, то потенциал проводника  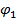зависит от его собственного заряда 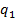и заряда :

.

 

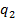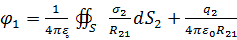В интегральном уравнении первого рода (24) появилось дополнительное слагаемое, которое представляет собой известную функцию координат и не оказывает существенного влияния на решение задачи.

     Если рядом с заряженным проводником находится другой заряженный проводник, то на поверхности первого проводника(т.1є )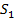

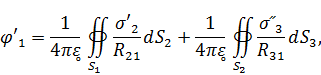
а на поверхности второго(т.1є )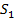

.

 

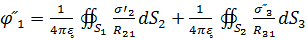Если известны потенциалы проводников φ ׳ и φ ״, то два последних уравнения образуют систему интегральных уравнений первого рода относительно плотности заряда на каждом из проводников σ׳(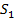) и σ״().

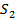     Если проводник находится во внешнем электрическом поле 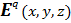, то интегральное уравнение второго рода (27) приобретает дополнительное слагаемое

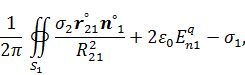
где 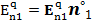 - нормальная составляющая напряженности внешнего поля в точке наблюдения 1 на поверхности проводника. Так как коэффициент перед интегральным оператором 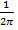равен его характеристическому числу, то к решению неоднородного интегрального уравнения (28) можно добавить решение однородного уравнения(27), умноженную на произвольную постоянную.

     Решение интегрального уравнения (28) можно получить как сумму его частного решения σ'(x,y,z)  ,удовлетворяющего условию

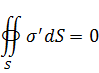
И решение однородного уравнения (27) σ ̋(x,y,z)  ,нормированного условием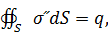                

где q - заданный заряд проводника. Частное решение дает распределение заряда на незаряженном проводнике под действием внешнего поля, решение однородного уравнения дает распределение заряда q по поверхности проводника при отсутствии внешнего поля.

     Если уравнение (28) и(27) решаются численными методами путем замены интеграла конечной суммой, то соответствующие системы алгебраических уравнений имеют определители, практически равные нулю. Чтобы обеспечить единственность решения уравнения (28), можно в соответствующей системе алгебраических уравнений заменить одно из её уравнений конечно-разностным соотношением, представляющим условие (29). Аналогично при решении однородного уравнения (27) можно ввести в систему алгебраических уравнений конечно-разностное соотношение, соответствующее условию (30).

     В системе двух заряженных проводников электрическое поле описывается системой двух интегральных уравнений второго рода. Одно из них получается из выражения для напряженности электрического поля, когда точка наблюдения помещается на поверхность первого проводника, второе, -когда точка наблюдения оказывается на поверхности второго проводника.

     Краткое содержание шестой лекции.

Электрическое поле в пространстве между заряженными проводниками удовлетворяет уравнению Лапласа 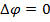 для потенциала 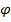. Поверхности проводников u, может быть, поверхность бесконечно большого радиуса ограничивают область существования поля. Если на этих поверхностях задать значения потенциала (на бесконечности 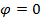), то получается краевая задача Дирихле.

Если по условию задачи заданы заряды проводников, то приходится решать столько краевых задач, сколько потенциальных коэффициентов в системе заряженных тел. Решения этих задач позволяют, во-первых, найти потенциальные коэффициенты и потенциалы проводников, соответствующие их заряда, во-вторых, скомбинировать решение исходной задачи из решения уже решенных частных задач.

Из выражения для потенциала заряженных проводников

 

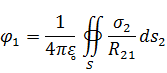
получается интегральное уравнение первого рода, если точку наблюдения поместить на поверхность S и прировнять потенциал в этой точке заданной величине.

Из выражения для напряженности электрического поля

 

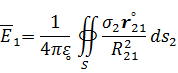
получается интегральное уравнение второго ряда, если точку наблюдения поместить на поверхность проводника S и прировнять среднее значение нормальной составляющей напряженности в этой точке величине, пропорциональной искомой плотности заряда:

.

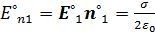Если заданы заряды в системе проводников, то с помощью интегральных уравнений определяются потенциальные коэффициенты, а затем решение исходной задачи находится как линейная комбинация из решений уравнений, уже решенных при определении потенциальных коэффициентов.