Задача 1. У мамы 2 яблока и 3 груши. Каждый день в течение 5 дней подряд она выдает по одному фрукту. Сколькими способами это может быть сделано?
Задача 2. Предприятие может предоставить работу по одной специальности 4 женщинами, по другой - 6 мужчинам, по третьей - 3 работникам независимо от пола. Сколькими способами можно заполнить вакантные места, если имеются 14 претендентов: 6 женщин и 8 мужчин?
Задача 3. В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человека, при условии, что все они должны ехать в различных вагонах?
Задача 4. В группе 9 человек. Сколько можно образовать разных подгрупп при условии, что в подгруппу входит не менее 2 человек?
Задача 5. Группу из 20 студентов нужно разделить на 3 бригады, причем в первую бригаду должны входить 3 человека, во вторую — 5 и в третью — 12. Сколькими способами это можно сделать.
Задача 6. Для участия в команде тренер отбирает 5 мальчиков из 10. Сколькими способами он может сформировать команду, если 2 определенных мальчика должны войти в команду?
Задача 7. В шахматном турнире принимали участие 15 шахматистов, причем каждый из них сыграл только одну партию с каждым из остальных. Сколько всего партий было сыграно в этом турнире?
Задача 8. Сколько различных дробей можно составить из чисел 3, 5, 7, 11, 13, 17 так, чтобы в каждую дробь входили 2 различных числа? Сколько среди них будет правильных дробей?
Задача 9. Сколько слов можно получить, переставляя буквы в слове Гора и Институт?
Задача 10. Каких чисел от 1 до 1 000 000 больше: тех, в записи которых встречается единица, или тех, в которых она не встречается?
1 Задание. У мамы 2 яблока и 3 груши. Каждый день в течение 5 дней подряд она выдает по одному фрукту. Сколькими способами это может быть сделано? Решение. Имеем набор {я, я, г, г, г}. Всего перестановок пятиэлементного множества 5!, но мы не должны учитывать перестановки, в которых объекты одного типа меняются местами несколько раз, поэтому нужно поделить на возможное число таких перестановок: 2! · 3!. Получаем в итоге 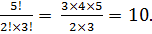
Ответ: 10 способов.
2. Задание. Предприятие может предоставить работу по одной специальности 4 женщинами, по другой - 6 мужчинам, по третьей - 3 работникам независимо от пола. Сколькими способами можно заполнить вакантные места, если имеются 14 претендентов: 6 женщин и 8 мужчин?
Решение.
Имеем 14 претендентов и 13 рабочих мест. Сначала выберем работников на первую специальность, то есть 4 женщин из 6: 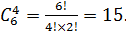
Далее независимо аналогичным образом выберем мужчин на вторую специальность: 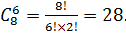
Осталось 2 женщины, 2 мужчин и 3 вакантных места, которые, по условию, могут занять любые из четырех оставшихся человек. Это может быть сделано 2 вариантами:
1. 1 женщина и 2 мужчин (выбираем женщину 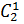 = 2 способами)
= 2 способами)
2. 1 мужчина и 2 женщины (выбираем мужчину 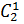 = 2 способами).
= 2 способами).
В итогt получаем 15 · 28(2 + 2) = 1680 способов.
Ответ: 1680 способов.
3 ЗАДАНИЕ. В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человека, при условии, что все они должны ехать в различных вагонах?
РЕШЕНИЕ.
Т.к. все пассажиры должны ехать в разных вагонах, требуется отобрать 4 вагона из 9 с учетом порядка (вагоны отличаются №), эти выборки – размещения из n различных элементов по m элементов, где n = 9, m = 4. Число таких размещений находим по формуле: 
Получаем: 
ОТВЕТ. 3024 способами можно рассадить в поезде 4 человека.
4 ЗАДАНИЕ. В группе 9 человек. Сколько можно образовать разных подгрупп при условии, что в подгруппу входит не менее 2 человек?
РЕШЕНИЕ.
Не менее 2-х человек, т.е. 2+7 или 3+6 или 4+5 человек (5+4, 6+3, 7+2 – те же самые комбинации). В каждой выборке важен только состав, т.к. члены подгруппы не различаются по ролям, т.е. выборки − сочетания из n различных элементов по m элементов, их число: 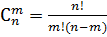 , где n!= 1⋅ 2 ⋅3⋅...⋅ n.
, где n!= 1⋅ 2 ⋅3⋅...⋅ n.
Число выборок из 2-х человек: 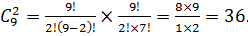
Число выборок из 3-х человек: 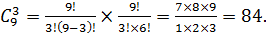
Число выборок из 4-х человек: 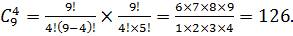
Применяем правило сложения: 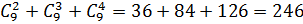 способов.
способов.
ОТВЕТ. 246 способов.
5 ЗАДАНИЕ. Группу из 20 студентов нужно разделить на 3 бригады, причем в первую бригаду должны входить 3 человека, во вторую — 5 и в третью — 12. Сколькими способами это можно сделать.
РЕШЕНИЕ.
Создавая первую бригаду, отбирают 3 человека из 20, создавая вторую – 5 из оставшихся 17, создавая третью – 12 из оставшихся 12. Для выборок важен только состав (роли членов бригады не различаются).
Эти выборки - сочетания из n различных элементов по m элементов, их число:
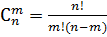 ,
,
Создавая сложную выборку (из 3-х бригад), воспользуемся правилом умножения:
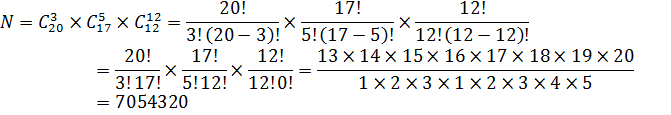
ОТВЕТ. 7054320 способов.
6 ЗАДАНИЕ. Для участия в команде тренер отбирает 5 мальчиков из 10. Сколькими способами он может сформировать команду, если 2 определенных мальчика должны войти в команду?
РЕШЕНИЕ.
Т.к. известно, что двое мальчиков войдут в команду, то остается отобрать 3 из 8. Для выборки важен только состав (по условию все члены команды не различаются по ролям). Следовательно, выборки – сочетания из n различных элементов по m элементов, их число: 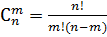 , где n!= 1⋅ 2 ⋅3⋅...⋅ n, при n = 8, m = 3.
, где n!= 1⋅ 2 ⋅3⋅...⋅ n, при n = 8, m = 3.
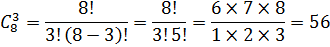
ОТВЕТ. 56 способов сформировать команду
7 ЗАДАНИЕ. В шахматном турнире принимали участие 15 шахматистов, причем каждый из них сыграл только одну партию с каждым из остальных. Сколько всего партий было сыграно в этом турнире?
РЕШЕНИЕ.
Способ 1. В одной игре участвуют 2 человека, следовательно, нужно вычислить, сколькими способами можно отобрать 2-х человек из 15, причем порядок в таких парах не важен. Воспользуемся формулой для нахождения числа сочетаний (выборок, отличающихся только составом) из n различных элементов по m элементов 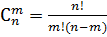 , где n!= 1⋅ 2 ⋅3⋅...⋅ n, при n =15, m =2.
, где n!= 1⋅ 2 ⋅3⋅...⋅ n, при n =15, m =2.
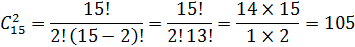
В процессе решения исключили 13! Из 15!, т.е. сократили произведение 15! = 1⋅ 2 ⋅3⋅...⋅15 на 13! = 1⋅ 2 ⋅ 3⋅...⋅13, остались после сокращения множители 14 и 15).
Способ 2. Первый игрок сыграл 14 партий (с2-м, 3-м, 4-м, и так до 15-го), 2- ой игрок сыграл 13 партий (3-м, 4-м, и т.д. до 15-го, исключаем то, что с первым партия уже была), 3-ий игрок − 12 партий, 4-ый − 11 партий, 5 – 10 партий, 6 – 9 партий, 7 – 8 партий, 8 – 7 партий,
9 – 6
10 – 5
11 – 4
12 – 3
13 – 2
14 – 1, а 15-ый уже играл со всеми.
Итого: 14+13+12+11+10+9+8+7+6+5+4+3+2+1=105 партий
ОТВЕТ. 105 партий.
8 ЗАДАНИЕ. Сколько различных дробей можно составить из чисел 3, 5, 7, 11, 13, 17 так, чтобы в каждую дробь входили 2 различных числа? Сколько среди них будет правильных дробей?
РЕШЕНИЕ.
Различных дробей из 6 чисел: 3, 5, 7, 11, 13, 17 можно составить

штук (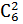 способами выбираем два числа из 6, и двумя способами составляем из них дробь: сначала одно число – числитель, другое знаменатель и наоборот). Из этих 30 дробей ровно 15 будут правильные (т.е., когда числитель меньше знаменателя):
способами выбираем два числа из 6, и двумя способами составляем из них дробь: сначала одно число – числитель, другое знаменатель и наоборот). Из этих 30 дробей ровно 15 будут правильные (т.е., когда числитель меньше знаменателя):
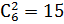
способами выбираем два числа из 6, и единственным образом составляем дробь так, чтобы числитель был меньше знаменателя.
ОТВЕТ. 30; 15.
9 ЗАДАНИЕ. Сколько слов можно получить, переставляя буквы в слове Гора и Институт?
РЕШЕНИЕ.
1) В слове «гора» четыре буквы, все они различны, поэтому можно получить всего N1 = 4! = 1 *2* 3 *4 = 24 различных слова.
2) В слове «институт» 8 букв, из них две буквы «и», три буквы «т» и по одной букве «н», «с» и «у». Поэтому всего можно получить перестановками букв
N2 = 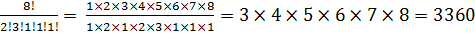
ОТВЕТ. 24 и 3360 слов.
10 ЗАДАНИЕ. Каких чисел от 1 до 1 000 000 больше: тех, в записи которых встречается единица, или тех, в которых она не встречается?
РЕШЕНИЕ. Подсчитаем количество чисел от 1 до 999999 (число 1 000 000 содержит единицу, его сразу отбросим), в записи которых нет единиц. Каждую цифру можно выбрать 9 способами (любая цифра кроме 1), поэтому все 6 цифр (по правилу произведения) можно выбрать 96 способами (если в числе до значащих цифр стоят нули, мы их просто отбрасываем). При этом один вариант (000000) нужно убрать, так как число 0 не рассматривается. Получаем всего N = 96 – 1 = 531440 чисел.
Так как всего чисел 1 000 000, то видно, что чисел без единицы среди чисел от 1 до 1 000 000 больше, чем тех, в записи которых единица есть.
 2020-04-12
2020-04-12 18450
18450






