В предыдущем разделе, совмещая табличное и последовательное расположения, мы
познакомились с примером так называемого вложенного расположения (nested layou:*»
основная идея которого очень проста — вы создаете несколько контейнеров с различ
ными менеджерами расположения, а затем добавляете их друг в друга для получения
искомого результата. Подбирая соответствующим образом менеджеры расположения, можно добиться абсолютно любого расположения компонентов.
В принципе, обычный пользовательский интерфейс вполне можно создать на основе
рассмотренных нами простейших расположений. Но, честно говоря, хотелось бы более гибкого подхода, особенно это касается расположения компонентов по вертикали. И потом, рассмотренные нами до этого
расположения очень неаккуратно работают с расстоянием между компонентами — его можно задать один раз, причем сразу для всех входящих в расположение компонентов. Между тем, в качественном интерфейсе расстояние между компонентами играет важнейшую роль, и чаще всего между разными компонентами оно разное. Поэтому создавать большую часть интерфейса с помощью этой идеи мы, конечно, не станем, а рассмотрим универсальные расположения, применяемые при создании пользовательского интерфейса чаще других.
| ti | 1 | 2 | 3 | 4 | 5 | 6 |
| yi | 1,25 | 1,14 | 1,18 | 1,20 | 1,25 | 1,00 |
| f(ti) | 1,2555 | 1,1441 | 1,1833 | 1,2024 | 1,2515 | 1,004 |
| ε(ti) | -0,0055 | -0,0041 | -0,0033 | -0,0024 | -0,0015 | -0,0004 |
| Поворотные точки | ||||||
| ti | 7 | 8 | 9 | 10 | 11 | 12 |
| yi | 0,99 | 1,04 | 1,06 | 1,10 | 1,20 | 1,35 |
| f(ti) | 0,9896 | 1,0388 | 1,0579 | 1,0969 | 1,1957 | 1,3441 |
| ε(ti) | 0,0004 | 0,0012 | 0,0021 | 0,0031 | 0,0043 | 0.0059 |
| Поворотные точки |
Систему уравнений (9) можно преобразовать к виду, в котором матрица системы будет симметричной. Для этого умножим i-е уравнение системы (9) на ci; получим систему уравнений 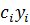 -λ
-λ 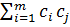 K(
K( ,
, 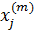 )
) 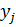 =
=  , i=1,…,m, (10)
, i=1,…,m, (10)
уже с симметричной матрицей.
Другой возможный способ симметризации состоит в следующем. Умножим i-е уравнение в (9) на 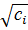 и положим
и положим 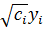 =
=  . Получим систему уравнений
. Получим систему уравнений
 -λ
-λ  K(
K( ,
, 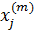 )
) 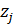 =
= 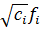 . (11)
. (11)
В случае Cj> 0 второй способ симметризации является более предпочтительным, поскольку разброс собственных значений у матрицы системы (11), как правило, меньше, чем у матрицы системы (10).
Заметим, что в случае, когда в квадратуре (6) все веса одинаковы:
 =…=
=…= 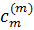 =(b-a)/m, (12)
=(b-a)/m, (12)
Необходимость в таких симметризациях отпадает.
Задача 1. Рассмотреть случай комплексного самосопряженного ядра
 K(x,s)=K(x,s). Проверить, что в этом случае при использовании описанных способов получается система уравнений с самосопряженным ядром.
K(x,s)=K(x,s). Проверить, что в этом случае при использовании описанных способов получается система уравнений с самосопряженным ядром.
Конечно, как и в случае решения произвольных систем линейных алгебраических уравнений, при использовании методов Гаусса или квадратного корня в процессе вычислений может возникнуть операция деления на нуль или переполнение.
 2020-04-07
2020-04-07 193
193







