2020-04-12
107
§1. Системы линейных уравнений: метод простых итераций, метод Зейделя
Задача: Дано: 
, i =1,..., m.
Найти: 
, удовлетворяющее системе.
Пусть система Крамеровская, т.е. m = n.
Запишем систему в матричной форме:
(1),
где 
– столбец неизвестных, 
– столбец свободных коэффициентов.
Метод простых итераций:
1. Преобразуем уравнение (1) в уравнение вида 
(2) (B=E-A);
2. Составим рекуррентную формулу: 
(3);
3. Выберем любое начальное приближение 
.
По формуле (3) найдем 
, 
, …, 
;
4. Если метод сходится, то последнее найденное приближение 
приблизительно равно решению системы (2).
Определения нормы вектора:
Опр. 1. 
.
Опр. 2.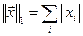 
.
Опр. 3. 
.
Определения нормы матрицы, согласованной с нормой вектора:
Опр. 
.
Следовательно:
Опр. 1. 
.
Опр. 2. 
.
Опр. 3. 
, где 
– собственное значение матрицы 
, 
– сопряженная к A матрица (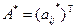
.
Замечание: Если 
уменьшается при 
, то метод простых итераций сходится.
Теорема. (Достаточное условие сходимости метода простых итераций)
Если || B || < 1, то система (2) имеет единственное решение, и итерационный процесс по формуле (3) сходится со скоростью убывающей геометрическое прогрессии.
Док-во:
1. Если 
– решение системы (2), то
.
Тогда однородная система 
имеет решение, удовлетворяющее
, т.е. решение существует (нулевой вектор) и единственное.
Следовательно система (2) имеет единственное решение (по теореме об общем решении СЛУ, равной сумме общего решения однородной системы и частного решения неоднородной).
2. Пусть 
– точное решение системы (2).
Тогда 
– погрешность на шаге k, и
; 
при 
.
Если обозначить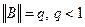 
, то норма погрешности меньше членов убывающей геометрической прогрессии с шагом q.
Теорема 2. (без док-ва) (Необходимое и достаточное условие сходимости метода простых итераций)
Пусть система (2) имеет единственное решение. Итерационный процесс по формуле (3) сходится к решению системы (2) при любом начальном приближении тогда и только тогда, когда все собственные значения матрицы B по модулю меньше 1.
Своеобразная модификация метода простых итераций – метод Зейделя.
Метод Зейделя:
Пусть в системе (1) в матрице A все диагональные элементы отличны от нуля.
1. Определим матрицы 
; 
.
Получим систему 
(4).
2. Построим рекуррентную формулу 
(5).
3. Выберем любое начальное приближение 
.
Система (5) имеет вид 
Из первого уравнения системы (5) найдем 
, из второго уравнения системы (5) найдем 
, и т.д. Таким образом, найдем 
. Аналогично, найдем 
, …, 
.
4. Если норма разности 
уменьшается, то метод сходится, и последнее найденное приближение 
приблизительно равно решению системы (4).
Замечание: Формула (5) равносильна формуле 
. Тогда 
. Итерационный процесс сходится, если все собственные значения матрицы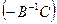 
по модулю меньше 1.
Теорема 3. (без док-ва)
Если A – вещественная, симметричная, положительно определенная (т.е. все главные миноры положительны) матрица, то метод Зейделя сходится.
§2. Метод наискорейшего спуска
Итерационные методы решения СЛУ сводятся к поиску вектора , минимизирующего функцию 
.
Воспользуемся теорией ФНП из мат.анализа:
– вектор, в направлении которого скорость возрастания 
наибольшая.
, где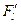 
– частная производная по переменной l.
Получаем рекуррентную формулу:
(6),
где 
– некоторый параметр, определяемый из условия:
.
Особый случай.
Пусть A – симметричная и положительно определенная матрица.
Пусть 
.
Точка минимума такой функции является решением уравнения 
.
Доказывается подстановкой и по определению – пропускаем.
Тогда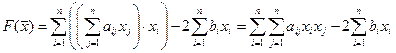 
.
.
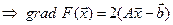
Пусть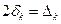 
.
, где 
– параметр, определяемый из условия:
.
Выведем формулу для нахождения .
Рассмотрим 
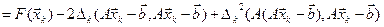
(т.к. A – симметричная, то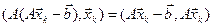 
Т.о. 
– квадратная функция с положительным коэффициентом при 
.
(т.к. A – положительно определенная, то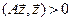 
для любого 
)
в точкеминимума.
– значение, при котором 
.
§ 3. Обратная интерполяция для решения нелинейных уравнений
Задача: Дано: f (x) = 0
Найти: x 0, такой, что f (x 0)=0.
Пусть точное решение x T Î [ a, b ] и f (x) обратима на [ a, b ], т.е. существует обратная функция g (x) = f –1(x): g (f (x))= x.
Тогда g (0)= g (f (x T))= x T.
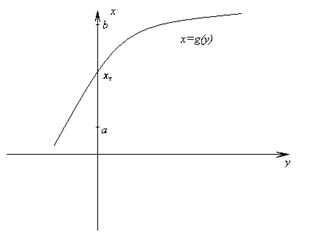
Алгоритм:
1) Выбрать [ a, b ]: f (x) обратима (монотонна).
2) Выбрать узлы x 0,..., x n Î [ a, b ].
Вычислить значения f (x) в узлах: f (x 0),..., f (x n).
3) Для g (x): f (x 0),..., f (x n) — узлы
x 0,..., x n — значения в узлах.
Найти интерполяционный многочлен Ln (x)» g (x).
4) Ln (0)» g (0) = x T — приближенное значение корня уравнения.
§ 4. Системы нелинейных уравнений: метод простых итераций
Задача: Дано: 
(7),
где 
– столбец неизвестных, 
– столбец, состоящий из скалярных функций от n переменных.
Метод простых итераций:
1) Преобразовать уравнение (7) в уравнение вида 
(8);
2) Составить рекуррентную формулу: 
(9);
3) Выбрать любое начальное приближение 
. По формуле (9) найти 
, 
, …, ;
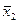4) Если норма разности 
уменьшается, то метод сходится, и последнее найденное приближение приблизительно равно решению системы (7).
Опр. Метрическое пространство H — множество, на котором задана функция метрики (расстояния) r (a, b), удовлетворяющая условиям:
1) r (a, b) ³ 0, и r (a, b) = 0 Û a = b;
2) r (a, b) = r (b, a);
3) r (a, b) + r (b,c) ³ r (a, c).
В нашем случае H = ú n, 
.
Опр. Отображением в метрическом пространстве называется функция
g: H ® H.
Опр. Отображение называется сжимающим, если существует число q:
0 ≤ q < 1, такое, что для любых x 1, x 2 Î H выполняется
r (g (x 1), g (x 2)) ≤ q × r (x 1, x 2).
Теорема.
Если отображение 
является сжимающим, то уравнение 
имеет единственное решение 
и 
.
Док-во:
1. Поскольку 
является сжимающим, то
(обозначили 
).
Тогда для l > k выполняется
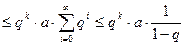
Т.о. при l ® ¥, k ® ¥ выполняется 
, следовательно последовательность 
, , …, 
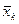,… сходится к предельному значению 
.
2. 
.
Это неравенство верно для любого k, т.е. 
меньше сколь угодно маленького положительного числа, т.е.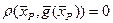 
.
Следовательно, 
— точное решение уравнения (8).
3. Предположим, что уравнение (8) имеет два точных решения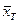 
и 
.
.
.
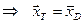Теорема доказана.
Частный случай. Пусть n = 1, т.е. система состоит из одного уравнения
f (x) = 0 с одной неизвестной x.
Уравнению равносильно x = g (x). Решение x T — точка пересечения графиков функций y = x и y = g (x).
x 1 = g (x 0), x 2 = g (x 1), …
На этом рисунке метод простых итераций сходится.
На следующем — нет.
Аналогом метода Зейделя является способ, когда координаты нового приближения 
вычисляются по очереди из одного уравнения системы:
.
§ 5. Системы нелинейных уравнений: метод Ньютона
Идея метода: Пусть 
— приближенное решение уравнения 
(7), достаточно близкое к искомому точному решению. В окрестности уравнение (7) заменяется линейным уравнением (вспомогательной линейной задачей), решение которого берется в качестве следующего приближения.
1 случай) m = 1, т.е. одно уравнение f (x) = 0 с одной неизвестной.
Пусть x0 — "хорошее" начальное приближение.
— линейное уравнение, заменяющее исходное
— решение линейного уравнения
— рекуррентная формула, метод Ньютона
Геометрическая иллюстрация метода:
На следующем рисунке показана ситуация зацикливания:
Общий случай)
Дано: 
(7)
Опр. Линейный оператор 
назовем производной отображения 
в точке , если 
при 
.
Действие линейного оператора 
совпадает с произведением матрицы A на вектор 
, где 
, 
, 
Пусть 
— точно решение уравнения (7);
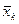— некоторое приближение, близкое к 
;
тогда 
.
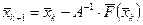рекуррентная формула, метод Ньютона.
Замечание: Матрица A –1 (зависящая от ) существует тогда и только тогда, когда A невырожденная.
Теорема (о сходимости метода Ньютона) (без док-ва)
При выполнении условий:
"аналог сжимаемости": 
для некоторого a 1 ≥ 0, любого 
и любого 
, где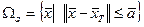 
;
"аналог дифференцируемости": 
, для некоторого a 2 ≥ 0, любых 
;
и при 
итерационный процесс Ньютона сходится с оценкой погрешности
.
§ 6. Методы спуска
По аналогии с методами спуска для системы линейных уравнений заменим задачу решения системы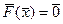 
(7) задачей минимизации функции 
.
Идея методов спуска:
1) Выбирается начальное приближение ;
2) Выбирается направление, в котором 
убывает;
3) В этом направлении от выбирается следующее приближение 
;
4) По рекуррентной формуле последовательно находят приближения ,…, ;
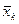5) Последнее приближение 
.
1 способ) Покоординатный спуск
Пусть 
.
Подставим в значения всех координат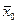 
, кроме первой переменной.
Получим функцию от одной переменной. Найдем ее точку минимума. Это будет x 1(1).
Затем подставим в x 1(1) и значения всех остальных координат 
, кроме второй переменной.
Получим функцию от одной переменной. Найдем ее точку минимума. Это будет x 1(2). Продолжая таким образом, получим 
. И т.д.
Проиллюстрируем поведение алгоритма для m = 2.
Модификации алгоритма:
1) Случайный покоординатный спуск — порядок переменных выбирается случайным образом.
2) "Метод муравьиной кучи" — покоординатный спуск выполняется для нескольких разных нулевых приближений.
Недостатки алгоритма:
1) Не гарантирует сходимости.
2) Не гарантирует приближение к глобальному экстремуму.
2 способ) Метод наискорейшего спуска.
Использует рекуррентную формулу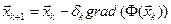 
, где 
– некоторый параметр, определяемый из условия:
.
3 способ) Условная минимизация
Задача: Найти точку 
, в которой достигается минимум 
, при условиях в виде неравенств или равенств:
Методы решения таких задач получили название математическое программирование.
Если все функции F, j, y являются линейными — линейное программирование. Если есть нелинейные функции — нелинейное программирование. Если искомое решение должно состоять из целых чисел — целочисленное программирование.
Глава V. Дифференциальные уравнения и системы
§ 1. Задача Коши для обыкновенных дифференциальных уравнений: применение формулы Тейлора
Задача Коши: Дано: 
— дифференциальное уравнение 1-го порядка;
— отрезок, на котором определена искомая y (x);
— начальное условие.
Найти: функцию y (x), удовлетворяющую уравнению и начальному условию.
Пусть f (x, y) — аналитическая в окрестности т.(x 0, y 0) (т.е. может быть представлена рядом по степеням (x – x 0) и (y – y 0).
Алгоритм:
1. Известна 
.
Найдем 
.
.
– – – – – – – – – – –
.
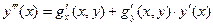2. Подставляя (x 0, y 0) получим:
.
.
. (числовые значения)
.
– – – – – – – – – – –
.
3. По формуле Тейлора составим:
Замечание: Пусть R — радиус сходимости ряда 
. Если 
, то погрешность формулы не уменьшается при 
.
Дальнейшее обобщение алгоритма:
Пусть отрезок разбит на n частей, 
— точки деления (узлы).
1. На 
найдем 
.
Тогда 
.
2. На 
найдем 
.
Тогда 
.
И т.д.
n. На 
найдем 
.
Тогда 
.
Т.е. найден набор 
приближенных значений искомой функции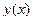 
в узлах 
.
§ 2. Метод Эйлера. Методы Рунге-Кутта
Пусть отрезок 
разбит на n частей,
— точки деления (узлы), 
.
При m = 1, формула из § 1 имеет вид:
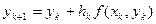— формула Эйлера.
Методы Рунге-Кутта — класс методов, включающий в себя метод Эйлера.
Общая идея методов:
Пусть даны параметры:
q, a2,…,aq; p 1,…, p q; bij, 0 < j < i £ q.
Найдем последовательно:
– – – – – – – – – – – – –
Тогда 
Т.е. 
находят последовательно по рекуррентной формуле
Частные случаи:
1) q = 1, p 1 = 1 — метод Эйлера.
2) q = 2, p 1 = 
= p 2; a2 = 1 = b21
Обоснование справедливости формулы:
Заменим интеграл квадратурной формулой трапеций
т.к. 
получаем
Заменим в правой части по формуле Эйлера
Тогда
3) q = 2, p 1 = 0, p 2 = 1; a2 = 
= b21
Обоснование справедливости формулы:
Заменим интеграл квадратурной формулой прямоугольников
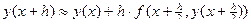
Заменим в правой части по формуле Эйлера
§ 3. Конечно-разностные методы
Задача: Дано:
Пусть отрезок 
разбит на n частей одинаковой длины h,
— узлы.
Найти: — значения y (x) в узлах.
Явные конечно-разностные методы используют соотношения вида
где коэффициенты 
, 
подбираются так, чтобы формула была точна для многочленов наивысшей степени.
Неявные конечно-разностные методы используют соотношения вида
где новое значение y k присутствует в обеих суммах.
Простейшие методы такого типа получаются на основе квадратурных формул интегрирования:
По формуле трапеций получаем
— неявный конечно-разностный метод.
Для использования формулы Симпсона применяют другое равенство
— неявный конечно-разностный метод.
Формулу прямоугольников применим также для равенства 
—явный конечно-разностный метод.
Замечание: вторая и третья формулы имеют низкую сходимость, т.е. при уменьшении h погрешность уменьшается медленнее, чем в первой формуле.
§ 4. Уравнения второго порядка
I. Дифференциальное уравнение, в котором отсутствует 
.
Задача Коши: Дано:
, 
– начальные условия
Пусть отрезок разбит на n частей одинаковой длины h,
— узлы.
Найти: — значения y (x) в узлах.
Для каждого узла выполняется
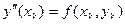
Заменим в левой части вторую производную формулой численного дифференцирования по трем точкам:
Правую часть заменим линейной комбинацией
Тогда получим формулу 
явный метод.
Если правую часть заменим другой линейной комбинацией 
, то получим формулу 
неявный метод.
Коэффициенты 
подбираются так, чтобы формула была точна для многочленов наивысшей степени.
Пример. Метод Нумерова — неявный метод, m = 1, четвертого порядка точности.
Вывод формулы методом неопределенных коэффициентов:
Нужно найти формулу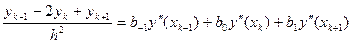 
точную для y (x), являющейся многочленом до четвертой степени.
Пусть x k = 0.
Для y (x) = x 2
Для y (x) = x 3
Для y (x) = x 4
Получается система
Решение системы: 
Применение метода:
1) По формуле Эйлера находим 
.
2) По рекуррентной формуле находим
.
II. Задача Коши: Дано:
, – начальные условия
отрезок разбит на n частей одинаковой длины h,
— узлы.
Найти: — значения y (x) в узлах.
В ходе решения будут найдены также 
значения 
в узлах.
Явный метод использует равенства
Неявный метод использует равенства
Пример. Явный метод, m = 0.
