Задание для 10А класса на 1 неделю карантина.
- Повторить параграф 28 в учебнике, разобраться с примерами в этом параграфе.
Решить номера в задачнике из параграфа 28 №№28.1-28.42 (под буквой а).
Не удивляйтесь, если встретятся решенные номера. Многие болели, поэтому задаю даже то, что в классе уже вместе прорешивали.
https://www.youtube.com/user/MathTutor777 это сайт с бесплатными видеоуроками. Кто не понимает, посмотрите еще раз тут объяснения тем.
- До 28 марта каждому нужно решить контрольную работу свой вариант (посмотрите внимательно кому что делать). Работа находится ниже, на следующей странице.
| 1 вариант | Ардашев Рыкова | 6 вариант | Ившин Стецура | 11 вариант | Нагорных |
| 2 вариант | Агафонова Садакова | 7 вариант | Калашников Субаева | 12 вариант | Николаева Усова |
| 3 вариант | Бекмансуров Садыкова | 8 вариант | Коршунова | 13 вариант | Нияматова |
| 4 вариант | Валеева Сорокина | 9 вариант | Косарева Шишкина | 14 вариант | Петров |
| 5 вариант | Жарова Сосновская | 10 вариант | Мерзлякова |
Фото своей подписанной (ФАМИЛИЯ ИМЯ КЛАСС постарайтесь, чтоб все было видно четко и ясно) работы отправляем мне удобным вам способом:
https://vk.com/shilyaeva1975 это моя страница вконтакте
shilyaeva.elena@mail.ru это мой адрес электронной почты
У кого нет возможности выслать, можете принести тетрадь в школу на проверку.
https://vk.com/club193278160 тут вы всегда найдете задания по математике
И еще, не оставляйте все на последний день, распределите задания поровну на всю неделю.
Удачи!
КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ: ПРОИЗВОДНАЯ
1 вариант
1. Найдите производные функций:
а) f(x) = 5х4 + 3х2 – 8х – 9; б) g(x) =  ;
;
в) q(x) =  ; г) u(x) = sin 5x
; г) u(x) = sin 5x
2. Точка движется по закону х(t)=3t3+2t+1 Найдите ускорение точки в момент времени 2сек.
3. Найдите угол наклона касательной к графику функции f(x)=  в точке х0=-1
в точке х0=-1
4. напишите уравнение касательной к графику функции f(x) = x2-2x в точке х0=2. Сделайте рисунок
 5. На рисунке изображены график функции
5. На рисунке изображены график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции  в точке
в точке 
6. Решите неравенство: 2х(х2-4)  < 0
< 0
2 вариант
1. Найдите производные функций:
а) f(x) = 3х5 + 2х3 – 4х – 3; б)g(x) =  ;
;
в) q(x) =  ; г) u(x) = cos 4x.
; г) u(x) = cos 4x.
2. Точка движется по закону х(t)=2t2+1 Найдите скорость точки в момент времени 2сек.
3. Найдите угол наклона касательной к графику функции f(x)= 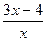 в точке х0=-2
в точке х0=-2
4. напишите уравнение касательной к графику функции f(x) = x2-1 в точке х0=-1. Сделайте рисунок
 5. На рисунке изображены график функции
5. На рисунке изображены график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции  в точке
в точке 
6. Решите неравенство: х(х2-2х+1)  ≥ 0
≥ 0
3 вариант
1. Найдите производные функций:
а) f(x) =  х5 + 3х3 – х – 4; б) g(x) =
х5 + 3х3 – х – 4; б) g(x) =  ;
;
в) q(x) =  ; г) u(x) =
; г) u(x) =  sin 5x
sin 5x
2. Точка движется по закону х(t)=2t3+4t Найдите ускорение точки в момент времени 2сек.
3. Найдите угол наклона касательной к графику функции f(x)=  в точке х0=2
в точке х0=2
4. напишите уравнение касательной к графику функции f(x) = x2-4 в точке х0=3. Сделайте рисунок
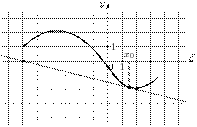 5. На рисунке изображены график функции
5. На рисунке изображены график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции  в точке
в точке 
6. Решите неравенство: (х2-2х)  ≤ 0
≤ 0
4 вариант
1. Найдите производные функций:
а) f(x) = - 2х6 +  х9 – 3; б)g(x) =
х9 – 3; б)g(x) = 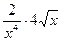 ;
;
в) q(x) =  ; г) u(x) =
; г) u(x) =  cos 4x.
cos 4x.
2. Точка движется по закону х(t)=t3+1 Найдите скорость точки в момент времени 3сек.
3. Найдите угол наклона касательной к графику функции f(x)=  в точке х0=1
в точке х0=1
4. напишите уравнение касательной к графику функции f(x) = x2+5 в точке х0=2. Сделайте рисунок
 5. На рисунке изображены график функции
5. На рисунке изображены график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции  в точке
в точке 
6. Решите неравенство: (-х2+1)  > 0
> 0
5 вариант
1. Найдите производные функций:
а) f(x) = 5х4 + 3х2 – 8х – 9; б) g(x) =  ;
;
в) q(x) =  ; г) u(x) = sin 5x
; г) u(x) = sin 5x
2. Точка движется по закону х(t)=t3-1 Найдите ускорение точки в момент времени 2сек.
3. Найдите угол наклона касательной к графику функции f(x)=  в точке х0=2
в точке х0=2
4. напишите уравнение касательной к графику функции f(x) = x2-1 в точке х0=-1. Сделайте рисунок
 5. На рисунке изображены график функции
5. На рисунке изображены график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции  в точке
в точке 
6. Решите неравенство:(х2+х-6)  < 0
< 0
6 вариант
1. Найдите производные функций:
а) f(x) = 3х5 + 2х3 – 4х – 3; б)g(x) =  ;
;
в) q(x) =  ; г) u(x) = cos 4x 2. Точка движется по закону х(t)= t3+5t Найдите, в какой момент времени скорость была равна 32м/с
; г) u(x) = cos 4x 2. Точка движется по закону х(t)= t3+5t Найдите, в какой момент времени скорость была равна 32м/с
3. Найдите угол наклона касательной к графику функции f(x)=sinx-7 в точке х0=2π
4. напишите уравнение касательной к графику функции f(x) = x2+2x в точке х0=1. Сделайте рисунок
 5. На рисунке изображены график функции
5. На рисунке изображены график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции  в точке
в точке 
6. Решите неравенство: (х2-1)  ≥ 0
≥ 0
7 вариант
1. Найдите производные функций:
а) f(x) =  х5 + 3х3 – х – 4; б) g(x) =
х5 + 3х3 – х – 4; б) g(x) =  ;
;
в) q(x) =  ; г) u(x) =
; г) u(x) =  sin 5x
sin 5x
2. Точка движется по закону х(t)= t4+1 Найдите скорость точки в момент времени 1сек.
3. Найдите угол наклона касательной к графику функции f(x)=  в точке х0=1
в точке х0=1
4. напишите уравнение касательной к графику функции f(x) = x2+3 в точке х0=1. Сделайте рисунок
 5. На рисунке изображены график функции
5. На рисунке изображены график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции  в точке
в точке 
6. Решите неравенство: (х+1)  < 0
< 0
8 вариант
1. Найдите производные функций:
а) f(x) = - 2х6 +  х9 – 3; б)g(x) =
х9 – 3; б)g(x) = 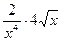 ;
;
в) q(x) =  ; г) u(x) =
; г) u(x) =  cos 4x
cos 4x
2. Точка движется по закону х(t)=2t3+1 Найдите в какой момент времени ускорение было 48м/с2
3. Найдите угол наклона касательной к графику функции f(x)=  в точке х0=3
в точке х0=3
4. напишите уравнение касательной к графику функции f(x) = 0,5x2-2x в точке х0=1. Сделайте рисунок
 5. На рисунке изображены график функции
5. На рисунке изображены график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции  в точке
в точке 
6. Решите неравенство: (х+1)  ≤ 0
≤ 0
9 вариант
1. Найдите производные функций:
а) f(x) = 5х4 + 3х2 – 8х – 9; б) g(x) =  ;
;
в) q(x) =  ; г) u(x) = sin 5x
; г) u(x) = sin 5x
2. Точка движется по закону х(t)=t3-4t Найдите скорость точки в момент времени 4сек.
3. Найдите угол наклона касательной к графику функции f(x)=  в точке х0=-1
в точке х0=-1
 4. напишите уравнение касательной к графику функции f(x) = 2x2+1 в точке х0=-1. Сделайте рисунок
4. напишите уравнение касательной к графику функции f(x) = 2x2+1 в точке х0=-1. Сделайте рисунок
5. На рисунке изображены график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции  в точке
в точке 
6. Решите неравенство: х(х2+2х+1)  < 0
< 0
10 вариант
1. Найдите производные функций:
а) f(x) = 3х5 + 2х3 – 4х – 3; б)g(x) =  ;
;
в) q(x) =  ; г) u(x) = cos 4x.
; г) u(x) = cos 4x.
2. Точка движется по закону х(t)=3t3+2. Найдите в какой момент времени ускорение было 27м/с2
3. Найдите угол наклона касательной к графику функции f(x)=  в точке х0=2
в точке х0=2
4. напишите уравнение касательной к графику функции f(x) = x2+x в точке х0=1. Сделайте рисунок
 5. На рисунке изображены график функции
5. На рисунке изображены график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции  в точке
в точке 
6. Решите неравенство: (х+1)  < 0
< 0
11 вариант
1. Найдите производные функций:
а) f(x) =  х5 + 3х3 – х – 4; б) g(x) =
х5 + 3х3 – х – 4; б) g(x) = 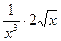 ;
;
в) q(x) = 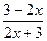 ; г) u(x) =
; г) u(x) =  sin 5x
sin 5x
2. Точка движется по закону х(t)= t2+2t Найдите в какой момент времени скорость была 68м/с
3. Найдите угол наклона касательной к графику функции f(x)=  в точке х0=1
в точке х0=1
4. напишите уравнение касательной к графику функции f(x) = x2-x в точке х0=2. Сделайте рисунок
 5. На рисунке изображены график функции
5. На рисунке изображены график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции  в точке
в точке 
6. Решите неравенство: (х2-4х+4) 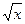 < 0
< 0
12 вариант
1. Найдите производные функций:
а) f(x) = - 2х6 +  х9 – 3; б)g(x) =
х9 – 3; б)g(x) =  ;
;
в) q(x) =  ; г) u(x) =
; г) u(x) =  cos 4x 2. Точка движется по закону х(t)=t2+5. Найдите в какой момент времени скорость была 74м/с
cos 4x 2. Точка движется по закону х(t)=t2+5. Найдите в какой момент времени скорость была 74м/с
3. Найдите угол наклона касательной к графику функции f(x)=  в точке х0=-1
в точке х0=-1
4. напишите уравнение касательной к графику функции f(x) = x2+1 в точке х0=1. Сделайте рисунок
 5. На рисунке изображены график функции
5. На рисунке изображены график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции  в точке
в точке 
6. Решите неравенство: х(х2+4х+4)  < 0
< 0
13 вариант
1. Найдите производные функций:
а) f(x) = 5х4 + 3х2 – 8х – 9; б) g(x) =  ;
;
в) q(x) =  ; г) u(x) = sin 5x
; г) u(x) = sin 5x
2. Точка движется по закону х(t)=2t3+1.Найдите в какой момент времени скорость точки была 54м/с
3. Найдите угол наклона касательной к графику функции f(x)=  в точке х0=2
в точке х0=2
4. напишите уравнение касательной к графику функции f(x) = x2-3x в точке х0=-1. Сделайте рисунок
 5. На рисунке изображены график функции
5. На рисунке изображены график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции  в точке
в точке 
6. Решите неравенство: (х+4)  < 0
< 0
14 вариант
1. Найдите производные функций:
а) f(x) =  х5 + 3х3 – х – 4; б) g(x) =
х5 + 3х3 – х – 4; б) g(x) = 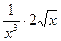 ;
;
в) q(x) = 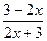 ; г) u(x) =
; г) u(x) =  sin 5x
sin 5x
2. Точка движется по закону х(t)= t3+2t+3 Найдите ускорение точки в момент времени 1сек.
3. Найдите угол наклона касательной к графику функции f(x)=  в точке х0=-1
в точке х0=-1
4. напишите уравнение касательной к графику функции f(x) = x2+2 в точке х0=-1. Сделайте рисунок
 5. На рисунке изображены график функции
5. На рисунке изображены график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции  в точке
в точке 
6. Решите неравенство: х(х+4) 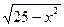 ≥ 0
≥ 0
 2020-04-12
2020-04-12 302
302






