Об оптимальном выборе шага

Константа q, фигурирующая в теореме 2. и характеризующая скорость сходимости метода, зависит от шага α. Нетрудно видеть, что величина

минимальна, если шаг α выбирается из условия |1 – αλ| = |1 – αΛ | (см. рис. 3), т. е. если α = α* = 2/(λ+ Λ). При таком выборе шага оценка сходимости будет наилучшей и будет характеризоваться величиной

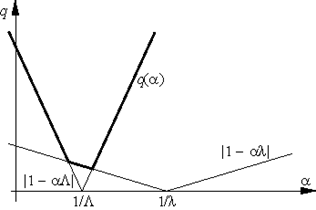
Рис. 3.

В качестве λ и Λ могут выступать равномерные по x оценки сверху и снизу собственных значений оператора f ′′(x). Если λ << Λ, то q * ≈ 1 и метод сходится очень медленно. Геометрически случай λ << Λ соответствует функциям с сильно вытянутыми линиями уровня (см. рис. 4). Простейшим примером такой функции может служить функция на R ², задаваемая формулой

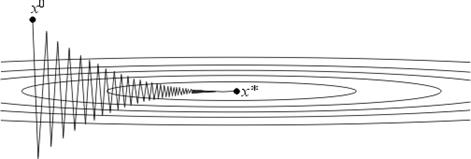
Рис. 4.

Поведение итераций градиентного метода для этой функции изображено на рис. 4 – они, быстро спустившись на "дно оврага", затем медленно "зигзагообразно" приближаются к точке минимума. Число μ = Λ/λ (характеризующее, грубо говоря, разброс собственных значений оператора f ′′(x)) называют числом обусловленности функции f. Если μ >> 1, то функции называют плохо обусловленными или овражными. Для таких функций градиентный метод сходится медленно.

Но даже для хорошо обусловленных функций проблема выбора шага нетривиальна в силу отсутствия априорной информации о минимизируемой функции. Если шаг выбирается малым (чтобы гарантировать сходимость), то метод сходится медленно. Увеличение же шага (с целью ускорения сходимости) может привести к расходимости метода. Опишем два алгоритма автоматического выбора шага, позволяющие частично обойти указанные трудности.