Построение трендовых моделей методом наименьших квадратов

Введение.

Задача построения трендовых моделей является частным случаем задачи аппроксимации таблично заданной функции применительно к рядам динамики. Задача прогнозирования решается путем экстраполяции статистических данных, полученных за прошлые периоды и представленных в виде ряда динамики, на будущие периоды времени. Экстраполяция осуществляется с использованием полученных трендовых моделей.

Цель лекции – изучить методику построения трендовых моделей методом наименьших квадратов и рассмотреть оценку точности прогнозов с использованием трендовых моделей.

 

Понятие тренда

Всякий ряд динамики теоретически может быть представлен в виде составляющих:

1) тренд – основная тенденция развития динамического ряда (к увеличению либо снижению его уровней);

2) циклические (периодические) колебания, в том числе сезонные;

3) случайные колебания.

Изучение тренда включает два основных этапа:

1) ряд динамики проверяется на наличие тренда;

2) производится выравнивание временного ряда и непосредственное выделение тренда с экстраполяцией полученных результатов.

Если по исходным статистическим данным непосредственно выделить наличие тренда в ряде динамики представляется затруднительным, то применяют так называемое сглаживание рядов динамики, которое может быть произведено тремя методами.

1. Укрупнение интервалов. Ряд динамики разделяют на некоторое достаточно большое число равных интервалов. Если средние уровни по интервалам не позволяют увидеть тенденцию развития явления, переходят к расчету уровней за большие промежутки времени, увеличивая длину каждого интервала (одновременно уменьшается количество интервалов).

2. Скользящая средняя. В этом методе исходные уровни ряда заменяются средними величинами, которые получают из данного уровня и нескольких симметрично его окружающих. Целое число уровней, по которым рассчитывается среднее значение, называют интервалом сглаживания. Интервал обычно выбирается нечетным (3, 5, 7 и т.д. точек). При нечетном сглаживании полученное среднее арифметическое значение закрепляют за серединой расчетного интервала.

3. Целью аналитического выравнивания динамического ряда является определение аналитической зависимости, описывающей изменение изучаемого явления во времени

Найденная аналитическая зависимость называется трендовой моделью.

Построение трендовой модели осуществляется в два этапа: на первом этапе по имеющемуся временному ряду (чаще всего представленному для наглядности графически) задают вид функции, на втором этапе находят неизвестные параметры функции.

Чаще всего для трендовых моделей используются следующие зависимости:

Одним из наиболее известных способов нахождения неизвестных коэффициентов а₀, а₁, а₂, … является метод наименьших квадратов (МНК).

 

Построение трендовых моделей методом наименьших квадратов

 

    Сформулируем первоначально задачу приближения по методу наименьших квадратов (МНК).

       Пусть в нескольких произвольных точках х_j (j = 1, 2, …m), принадлежащих отрезку [α, β], известны значения некоторой функции f(x_j) (аналитическое выражение функции может быть неизвестным). Требуется подобрать по возможности простую функцию  и ее параметры a_i, i=0,1,2,… так, чтобы сумма квадратов разностей заданной и приближающей функций была минимальной. При этом не требуется, чтобы значения обеих функций в точках х_j совпадали (рис.2.).

x

xm

xj

g(x)

f(x)

x1

g(x)

f(xj)–g(xj)

 

           

 

Рис.2.

       Таким образом, МНК основан на использовании дискретной нормы (численной меры) отклонения функции от ее приближения.

                              ,                     (3)

где x_j – фиксированные точки, в которых задана функция..

       Приведенное выражение часто называют целевой функцией МНК.

       МНК находит широкое применения при решении задач прогнозирования. Например, этот метод незаменим при статистической обработке рядов динамики и выявления тенденций развития изучаемого явления. При этом основной трудностью решения задачи аппроксимации на основе этого метода является проблема выбора подходящей эмпирической формулы (аппроксимирующей функции), так как не существует общего правила, обеспечивающего такой выбор. Во-первых, сам процесс может протекать так, что описать его аналитически невозможно, то есть не существует формулы, связывающей параметры процесса с его результатами. Во-вторых, объем исходных данных может быть недостаточным для правильного определения вида функции или погрешность опытных данных не позволяет сделать правильный выбор.

       В тех случаях, когда выбор аппроксимирующей функции уже сделан, определение ее параметров большой проблемы не составляет. Для этого требуется найти значения параметров, при которых норма отклонения R(a,a₁,a₂,…a_n) становится минимальной. Традиционно это делается методами математического анализа, то есть с помощью производных

              .                                (4)

    (Заметим, что для нахождения минимума целевой функции могут использоваться другие, например, численные методы)

       Возможно, что определенную трудность может вызвать процедура дифференцирования выражений, содержащих знак суммы. Однако, также как и предыдущем случае операцию дифференцирования можно внести под знак суммы

- - - - - - - -

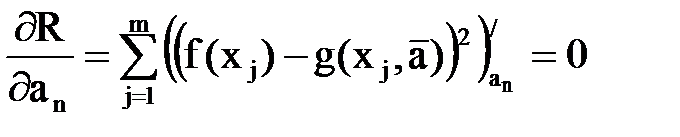
    Для простоты опустим вывод и приведем конечные формулы, используемые при линейной g(x) = a₀ + a₁x и квадратичной g(x) = a₀ + a₁x + a₂x² аппроксимации функций по методу наименьших квадратов

 

Линейная                                      Квадратичная

         

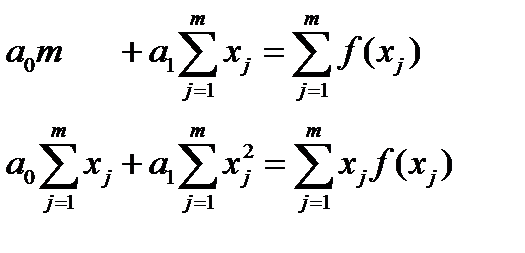
Построив уравнение регрессии, проводят оценку его надежности. Это делается посредством критерия Фишера (F). Фактический уровень (F_факт) сравнивается с критическим (табличным) значением:

где: k – число параметров функции, описывающей тенденцию;

   n – число уровней ряда;

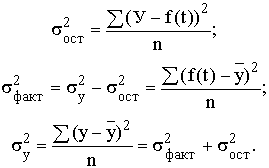
F_факт сравнивается с F_кр при n₁ = (k-1), n₂ = (n-k) степенях свободы и уровне значимости a (обычно a = 0,05). Если F_факт > F_кр, уравнение регрессии значимо, т.е. построенная модель адекватна фактической временной тенденции.

В Excel F_кр =F.ОБР(g, n₁, n₂), где g = (1-a) - надежность оценки.