2020-04-20
543
Рассмотрим участок проводника постоянного сечения S с постоянным током I. Предположим, что свободные носители заряда имеют одинаковую скорость направленного движения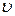 
. Тогда за время 
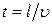все свободные заряды, находящиеся в данный момент в участке проводника, ограниченном сечениями S 1 и S 2, пересекут сечение S 2. Свободные носители заряда перенесут через сечение общий заряд 
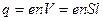, где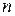 
– концентрация свободных носителей заряда, 
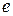– заряд одной частицы, 
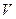– объём проводника, ограниченного сечениями S 1 и S 2, поскольку площадь сечения постоянна 
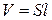. Сила тока численно равна заряду, протекающему через поперечное сечение (
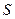) в единицу времени 
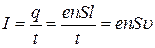. По определению плотность тока (
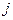) связана с силой тока 
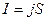. Откуда для плотности тока 
.
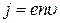Концентрация равна количеству частиц в единице объёма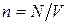 
.
Если предположить, что в кристаллической решётке металла свободным становится только один валентный электрон каждого атома, то концентрацию электронов в металле можно оценить, зная его плотность (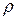
) и молярную массу (
)
,
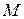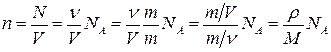где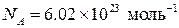 
– постоянная Авогадро.
Закон Ома для участка цепи: сила тока в цепи прямо пропорциональна приложенному напряжению
; 
.
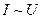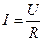Закон Ома в дифференциальной форме.
Закон Ома для бесконечно малого участка проводника длиной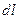 
, площадью сечения 
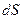имеет вид 
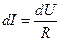, сопротивление бесконечно малого участка проводника 
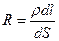, разность потенциалов 
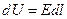, откуда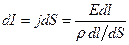 
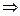
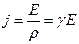. Это закон Ома в дифференциальной форме, 
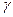– удельная проводимость.
Удельная проводимость металлов при комнатной температуре 6×103-6×105 Ом-1∙см-1, вещества с проводимостью 104-10-10 Ом-1∙см-1 относят к классу полупроводников, вещества с проводимостью 10-10-10-20 Ом-1∙см-1 – к классу диэлектриков.
Изучение закона Ома и определение удельного сопротивления нихромовой проволоки.
Необходимо знать пункты из лаб.раб. “Порядок выполнения работы” и “Порядок измерений. Обработка результатов измерений”. Описание лаб.раб. дано ниже.
Лабораторная работа 1
