Министерство образования и науки Российской Федерации
 |
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ПЕТРА ВЕЛИКОГО
 |
А. М. ХАХИНА
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
ОПОРНЫЙ КОНСПЕКТ
Учебное пособие
Санкт-Петербург
Издательство Политехнического университета
2020
Р е ц е н з е н т – преподаватель математики СПбГБПОУ
«Колледж «ПетроСтройСервис» И. В. Хахин
Хахина А. М. Математическая статистика: учеб. пособие / А. М. Хахина. — СПбПУ, 2020. — 67 с.
В пособии приведены теоретические сведения и формулы по дисциплине «Математическая статистика».
Теоретический материал снабжен большим количеством примеров.
Предназначено для студентов всех форм обучения (очной, вечерней и заочной) при подготовке бакалавров и дипломированных специалистов.
© Хахина А. М., 2020
© Санкт-Петербургский государственный
политехнический университет, 2020
1. Элементы математической статистики
Первая задача математической статистики – указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально поставленных экспериментов.
Вторая задача математической статистики - разработать методы анализа статистических данных в зависимости от целей исследования. Сюда относятся:
a) оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости случайной величины от одной или нескольких случайных величин и др.;
б) проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого известен.
Современная математическая статистика разрабатывает способы определения числа необходимых испытаний до начала исследования (планирование эксперимента), в ходе исследования (последовательный анализ) и решает многие другие задачи. Современную математическую статистику определяют, как науку о принятии решений в условиях неопределенности.
1.1. Генеральная и выборочная совокупности
Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты. Например, если имеется партия деталей, то качественным признаком может служить стандартность детали, а количественным - контролируемый размер детали.
Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов.
Генеральной совокупностью называют совокупность объектов, из которых производится выборка.
Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности. Например, если из 2000 деталей отобрано для обследования 500 деталей, то объем генеральной совокупности N = 2000, объем выборки n = 500.
1.2. Репрезентативная выборка
Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.
Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.
На практике обычно пользуются бесповторным случайным отбором.
Для того чтобы по данным выборки можно было достаточно уверенно судить об интересующем признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли. Другими словами, выборка должна правильно представлять пропорции генеральной совокупности. Это требование коротко формулируют так: выборка должна быть репрезентативной (представительной).
В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если ее осуществить случайно: каждый объект выборки отобран случайно из генеральной совокупности, если все объекты имеют одинаковую вероятность попасть в выборку.
Если объем генеральной совокупности достаточно велик, а выборка составляет лишь незначительную часть этой совокупности, то различие между повторной и бесповторной выборками стирается.
1.3. Способы отбора
1. Отбор, не требующий расчленения генеральной совокупности на части. Сюда относятся: а) простой случайный бесповторный отбор; б) простой случайный повторный отбор.
2. Отбор, при котором генеральная совокупность разбивается на части. Сюда относятся: а) типический отбор; б) механический отбор; в) серийный отбор.
Простым случайным называют такой отбор, при котором объекты извлекают по одному из всей генеральной совокупности. Осуществить простой отбор можно различными способами. Например, для извлечения n объектов из генеральной совокупности объема N поступают так: выписывают номера от 1 до N на карточках, которые тщательно перемешивают, и наугад вынимают одну карточку; объект, имеющий одинаковый номер с навлеченной карточкой, подвергают обследованию; затем карточку возвращают в пачку и процесс повторяют, т. е, карточки перемешивают, наугад вынимают одну из них и т. д. Так поступают раз; в итоге получают простую случайную повторную выборку объема n. Если извлеченные карточки не возвращать в пачку, то выборка является простой случайной бесповторной.
Типическим называют отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой ее «типической» части. Например, если детали изготовляют на нескольких станках, то отбор производят не из всей совокупности деталей, произведенных всеми станками, а из продукции каждого станка в отдельности. Типическим отбором пользуются тогда, когда обследуемый признак заметно колеблется в различных типических частях генеральной совокупности. Например, если продукция изготовляется на нескольких машинах, среди которых есть более и менее изношенные, то здесь типический отбор целесообразен.
Механическим называют отбор, при котором генеральную совокупность «механически» делят на столько групп, сколько объектов должно войти в выборку, а из каждой группы отбирают один объект.
Серийным называют отбор, при котором объекты отбирают из генеральной совокупности не по одному, а "сериями", которые подвергаются сплошному обследованию. Например, если изделия изготовляются большой группой станков-автоматов, то подвергают сплошному обследованию продукцию только нескольких станков. Серийным отбором пользуются тогда, когда обследуемый признак колеблется в различных сериях незначительно.
Подчеркнем, что на практике часто применяется комбинированный отбор, при котором сочетаются указанные выше способы.
1.4. Статистическое распределение выборки
Пусть из генеральной совокупности извлечена выборка, причем х1, наблюдалось n1 раз, x2 – n2 раз, xk – nk раз и ∑ni = n - объем выборки. Наблюдаемые значения хi, называют вариантами, а последовательность вариант, записанных в возрастающем порядке, - вариационным рядом. Числа наблюдений называют частотами, их отношения к объему выборки ni/n = Wi - относительными частотами.
Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот. Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).
В случае, когда число значений признака (с. в. Х) велико или принак является непрерывным (т. е. когда с. в. Х может принять любое значение в некотором интервале), составляют интервальный статистический ряд. В первую строку таблицы статистического распределения вписывают частичные промежутки [x0, x1), [x1, x2), …, [xk-1, xk), которые берут обычно одинаковыми по длине: h = x1 – x0 = x2 - x1 = … Для определения величины интервала (h) можно использовать формулу Стерджеса:
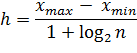
где xmax - xmin - разность между наибольшим и наименьшим значениями признака, m = 1 + log2n - число интервалов (log2n ≈ 3,322 lg n).
За начало первого интервала рекомендуется брать величину xнач = xmin - 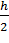 .
.
1.5. Эмпирическая функция распределения
Пусть известно статистическое распределение частот количественного признака X. Введем обозначения: nx - число наблюдений, при которых наблюдалось значение признака, меньшее х; n - общее число наблюдений (объем выборки). Ясно, что относительная частота события X < x равна nx/n. Если х изменяется, то, вообще говоря, изменяется и относительная частота, т.е. относительная частота nx/n есть функция от х. Так как эта функция находится эмпирическим (опытным) путем, то ее называют эмпирической.
Эмпирической функцией распределения (функцией распределения выборки) называют функцию F* (x), определяющую для каждого значения х относительную частоту события X < x.
Итак, по определению,
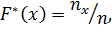
где nx - число вариант, меньших х; n-объем выборки.
Таким образом, для того чтобы найти, например, F*(x2), надо число вариант, меньших х2, разделить на объем выборки:
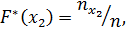
В отличие от эмпирической функции распределения выборки функцию распределения F(x) генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями состоит в том, что теоретическая функция F(x) определяет вероятность события X < x, a эмпирическая функция F*(x) определяет относительную частоту этого же события. Из теоремы Бернулли следует, что относительная частота события X < х, т. е. F*(x) стремится по вероятности к вероятности F(x) этого события. Другими словами, при больших числах F*(x) и F (x) мало отличаются одно от другого в том смысле, что 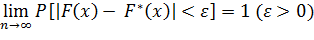 . Уже отсюда следует целесообразность использования эмпирической функции распределения выборки для приближенного представления теоретической (интегральной) функции распределения генеральной совокупности.
. Уже отсюда следует целесообразность использования эмпирической функции распределения выборки для приближенного представления теоретической (интегральной) функции распределения генеральной совокупности.
Такое заключение подтверждается и тем, что F*(x) обладает всеми свойствами F(x). Из определения функции F*(x) вытекают следующие ее свойства:
1) значения эмпирической функции принадлежат отрезку [0, 1];
2) F*(x) - неубывающая функция;
3) если х1 - наименьшая варианта, то F*(x) = 0 при x <= x1; если xk –
наибольшая варианта, то F*(x) = 1 при x > xk.
Итак, эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.
1.6. Полигон и гистограмма
Полигоном частот называют ломаную, отрезки которой соединяют точки (x1; n1), (x2; n2), …, (xk; nk). Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат-соответствующие им частоты n1. Точки (xi; n1) соединяют отрезками прямых и получают полигон частот.
Полигоном относительных частот называют ломаную, отрезки которой соединяют точки (x1; W1), (x2; W2), … (xk, Wk). Для построения полигона относительных частот на оси абсцисс откладывают варианты хi, а на оси ординат-соответствующие им относительные частоты Wi. Точки (xi; Wi) соединяют отрезками прямых и получают полигон относительных частот.
B случае непрерывного признака целесообразно строить гистограмму, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала ni- сумму частот вариант, попавших в i-й интервал.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, a высоты равны отношению ni/h (плотность частоты).
Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии ni/h.
Площадь i-ro частичного прямоугольника равна hni/h = ni - сумме частот вариант i-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т. е. объему выборки.
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению Wi/h (плотность относительной частоты).
Площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.
2. Статистические оценки параметров распределения
Пусть требуется изучить количественный признак генеральной совокупности. Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет признак. Естественно возникает задача оценки параметров, которыми определяется это распределение. Например, если наперед известно, что изучаемый признак распределен в генеральной совокупности нормально, то необходимо оценить (приближенно найти) математическое ожидание и среднее квадратическое отклонение, так как эти два параметра полностью определяют нормальное распределение; если же есть основания считать, что признак имеет, например, распределение Пуассона, то необходимо оценить параметр А, которым это распределение определяется.
Обычно в распоряжении исследователя имеются лишь данные выборки, например значения количественного признака х1, х2,..., xn, Полученные в результате п наблюдений (здесь и далее наблюдения предполагаются независимыми). Через эти данные и выражают оцениваемый параметр. Рассматривая х1, х2,..., хn как независимые случайные величины Х1, Х1,..., Xn, можно сказать, что найти статистическую оценку неизвестного параметра теоретического распределения — это значит найти функцию от наблюдаемых случайных величин, которая и дает приближенное значение оцениваемого параметра. Например, как будет показано далее, для оценки математического ожидания нормального распределения служит функция (среднее арифметическое наблюдаемых значений признака)
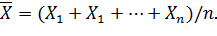
Итак, статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин.
2.1. Несмещенные, эффективные и состоятельные оценки
Для того чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям. Ниже указаны эти требования.
Пусть Θ*— статистическая оценка неизвестного параметра Θ теоретического распределения. Допустим, что по выборке объема n найдена оценка 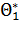 . Повторим опыт, т. е. извлечем из генеральной совокупности другую выборку того же объема и по ее данным найдем оценку
. Повторим опыт, т. е. извлечем из генеральной совокупности другую выборку того же объема и по ее данным найдем оценку  :. Повторяя опыт многократно, получим числа
:. Повторяя опыт многократно, получим числа 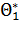 ,
,  ,...,
,..., 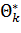 , которые, вообще говоря, различны между собой. Таким образом, оценку
, которые, вообще говоря, различны между собой. Таким образом, оценку 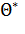 можно рассматривать как случайную величину, а числа
можно рассматривать как случайную величину, а числа 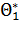 ,
,  ,...,
,..., 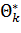 ,— как ее возможные значения.
,— как ее возможные значения.
Представим себе, что оценка 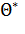 дает приближенное значение
дает приближенное значение 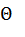 с избытком; тогда каждое найденное по данным выборок число
с избытком; тогда каждое найденное по данным выборок число 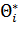 ; (i=1,2,..., k) больше истинного значения
; (i=1,2,..., k) больше истинного значения 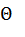 . Ясно, что в этом случае и математическое ожидание (среднее значение) случайной величины
. Ясно, что в этом случае и математическое ожидание (среднее значение) случайной величины 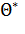 больше, чем
больше, чем 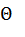 , т. е. М(
, т. е. М(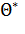 ) >
) > 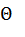 . Очевидно, что если
. Очевидно, что если 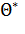 дает оценку с недостатком, то М(
дает оценку с недостатком, то М(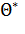 ) <
) < 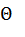 .
.
Таким образом, использование статистической оценки, математическое ожидание которой не равно оцениваемому параметру, привело бы к систематическим (одного знака) ошибкам. По этой причине естественно потребовать, чтобы математическое ожидание оценки 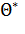 было равно оцениваемому параметру. Хотя соблюдение этого требования не устранит ошибок (одни значения
было равно оцениваемому параметру. Хотя соблюдение этого требования не устранит ошибок (одни значения 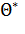 больше, а другие меньше
больше, а другие меньше 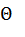 ), однако ошибки разных знаков будут встречаться одинаково часто. Иными словами, соблюдение требований М(
), однако ошибки разных знаков будут встречаться одинаково часто. Иными словами, соблюдение требований М(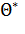 ) =
) = 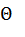 гарантирует от получения систематических ошибок.
гарантирует от получения систематических ошибок.
Несмещенной называют статистическую оценку 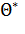 , математическое ожидание которой равно оцениваемому параметру
, математическое ожидание которой равно оцениваемому параметру 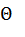 при любом объеме выборки, т. е. М(
при любом объеме выборки, т. е. М(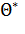 ) =
) = 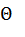 .
.
Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.
Эффективной называют статистическую оценку, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию.
При рассмотрении выборок большого объема (n велико!) к статистическим оценкам предъявляется требование состоятельности.
Состоятельной называют статистическую оценку, которая при 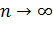 стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при
стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при 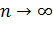 cтремится к нулю, то такая оценка оказывается и состоятельной.
cтремится к нулю, то такая оценка оказывается и состоятельной.
2.2. Генеральная средняя
Генеральной средней 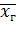 , называют среднее арифметическое значений признака генеральной совокупности.
, называют среднее арифметическое значений признака генеральной совокупности.
Если все значения х1, х2,..., xn признака генеральной совокупности объема N различны, то
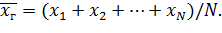
Если же значения признака х1, х2,..., xk имеют соответственно частоты N1, N2,..., Nk причем N1+N2+…+Nk=N, то
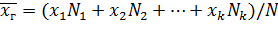
т.е. генеральная средняя есть средняя взвешенная значений признака с весами, равными соответствующим частотам.
Выборочной средней 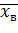 , называют среднее арифметическое значение признака выборочной совокупности.
, называют среднее арифметическое значение признака выборочной совокупности.
Если все значения х1, х2,..., xk признака выборки объема n различны, то
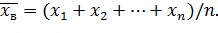
Если же значения признака х1, х2,..., xk имеют соответственно частоты n1, n2,..., nk причем n1 + n2 +... + nk = n, то
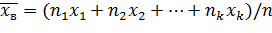 .
.
Или 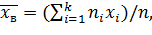
т.е. выборочная средняя есть средняя взвешенная значений признака с весами, равными соответствующим частотам.
2.3. Групповая и общая средние
Групповой средней называют среднее арифметическое значений признака, принадлежащих группе.
Общей средней 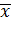 называют среднее арифметическое значений признака, принадлежащих всей совокупности.
называют среднее арифметическое значений признака, принадлежащих всей совокупности.
Зная групповые средние и объемы групп, можно найти общую среднюю: общая средняя равна средней арифметической групповых средних, взвешенной по объемам групп.
2.4. Отклонение от общей средней и его свойство
Рассмотрим совокупность, генеральную или выборочную, значений количественного признака Х объема n:
значения признака...... х1, х2,..., xk
частоты............... n1, n2,..., nk
При этом 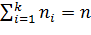 . Далее для удобства записи знак суммы
. Далее для удобства записи знак суммы 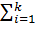 заменен знаком ∑.
заменен знаком ∑.
Найдем общую среднюю:
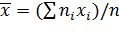 .
.
Отсюда
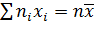 . (*)
. (*)
Заметим, что поскольку 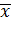 — постоянная величина, то
— постоянная величина, то
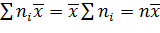 . (**)
. (**)
Отклонением называют разность хi — 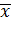 между значением признака и общей средней.
между значением признака и общей средней.
Теорема. Сумма произведений отклонений на соответствующие частоты равна нулю:
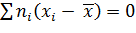 .
.
Доказательство. Учитывая (*) и (**), получим
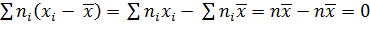 .
.
Следствие. Среднее значение отклонения равно нулю. Действительно,
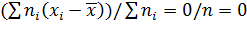 .
.
2.5. Генеральная дисперсия
Генеральной дисперсией D г называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения xг.
Если все значения х1, х2,..., xN признака генеральной совокупности объема N различны, то
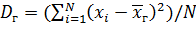 .
.
Если же значения признака х1, х2,..., xk имеют соответственно частоты N1, N2,..., Nk причем N1 + N2 +... + Nk, то
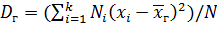 ,
,
т. е. генеральная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.
Генеральным средним квадратическим отклонением (стандартом) называют квадратный корень из генеральной дисперсии:
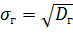 .
.
2.6. Выборочная дисперсия
Выборочной дисперсией Dв называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения 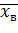 .
.
Если все значения х1, х2,..., xn признака выборки объема n различны, то
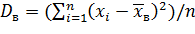 .
.
Если же значения признака х1, x2,..., xk имеют соответственно частоты n1, n2, …, nk, причем n1 + n2 + … + nk=n, то
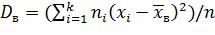 ,
,
т. е. выборочная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.
Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень из выборочной дисперсии:
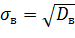 .
.
2.7.Формула для вычисления дисперсии
Теорема. Дисперсия равна среднему квадратов значений признака минус квадрат общей средней:
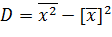 .
.
Доказательство. Справедливость теоремы вытекает из преобразований:
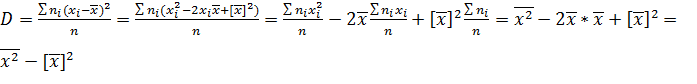 .
.
Итак,
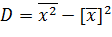 ,
,
где 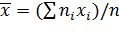 ,
, 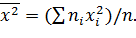
2.8. Групповая, внутригрупповая, межгрупповая и общая дисперсии
Групповой дисперсией называют дисперсию значений признака, принадлежащих группе, относительно групповой средней
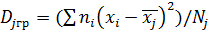 ,
,
где ni— частота значения хi; j— номер группы; 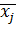 — групповая средняя группы j;
— групповая средняя группы j; 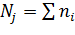 — объем группы j.
— объем группы j.
Внутригрупповой дисперсией называют среднюю арифметическую дисперсий, взвешенную по объемам групп:
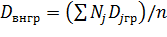 ,
,
где Nj — объем группы j; n= 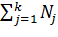 — объем всей совокупности.
— объем всей совокупности.
Межгрупповой дисперсией называют дисперсию групповых средних относительно общей средней:
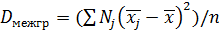 ,
,
где 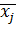 — групповая средняя группы j; Nj — объем группы j;
— групповая средняя группы j; Nj — объем группы j; 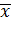 — общая средняя; n =
— общая средняя; n = 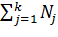 — объем всей совокупности.
— объем всей совокупности.
Общей дисперсией называют дисперсию значений признака всей совокупности относительно общей средней:
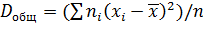 ,
,
где ni, — частота значения хi; 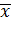 — общая средняя; n — объем всей совокупности
— общая средняя; n — объем всей совокупности
2.9. Сложение дисперсий
Теорема. Если совокупность состоит из нескольких групп, то общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий:
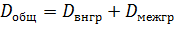 .
.
Доказательство. Для упрощения доказательства предположим, что вся совокупность значений количественного признака Х разбита на две следующие группы:
Группа........ первая вторая
Значение признака... x1 x2 x1 x2
Частота........ m1 m2 n1 n2
Объем группы.... N1=m1+m2 N2=n1+n2
Групповая средняя... 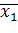
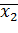
Групповая дисперсия.. D1гр D2гр
Объем своей совокупности n=N1 + N2
Найдем общую дисперсию:
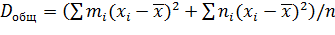 . (*)
. (*)
Преобразуем первое слагаемое числителя, вычтя и прибавив 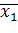 :
:
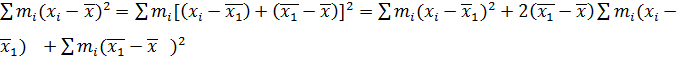 .
.
Так как
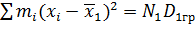 .
.
(равенство следует из соотношенияи 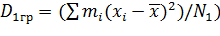 и в силу
и в силу
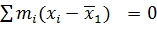 ,
,
то первое слагаемое принимает вид
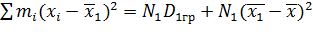 . (**)
. (**)
Аналогично можно представить второе слагаемое числителя (*) (вычтя и прибавив 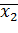 ):
):
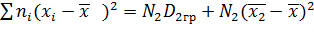 . (***)
. (***)
Подставим (**) и (***) в (*):
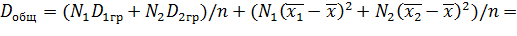
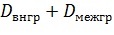 .
.
Итак,
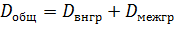 .
.
2.10. Оценка генеральной дисперсии по исправленной выборочной
Выборочная дисперсия является смещенной оценкой Dг, другими словами, математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно
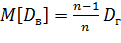 .
.
Легко «исправить» выборочную дисперсию так, чтобы ее математическое ожидание было равно генеральной дисперсии. Достаточно для этого умножить Dв, на дробь n/(n— 1). Сделав это, получим исправленную дисперсию, которую обычно обозначают через s2:
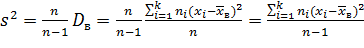 .
.
Исправленная дисперсия является, конечно, несмещенной оценкой генеральной дисперсии. Действительно,
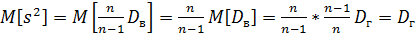 .
.
Итак, в качестве оценки генеральной дисперсии принимают исправленную дисперсию
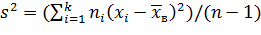 .
.
Для оценки же среднего квадратического отклонения генеральной совокупности используют «исправленное» среднее квадратическое отклонение, которое равно квадратному корню из исправленной дисперсии:
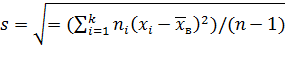 .
.
3. Точность оценки, доверительная вероятность (надежность)
3.1. Доверительный интервал
Точечной называют оценку, которая определяется одним числом. Все оценки, рассмотренные выше, — точечные. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т. е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.
Интервальной называют оценку, которая определяется двумя числами-концами интервала. Интервальные оценки позволяют установить точность и надежность оценок (смысл этих понятий выясняется ниже).
Пусть найденная по данным выборки статистическая характеристика Θ* служит оценкой неизвестного параметра Θ. Будем считать Θ постоянным числом (Θ может быть и случайной величиной). Ясно, что Θ* тем точнее определяет параметр Θ, чем меньше абсолютная величина разности |Θ — Θ*|. Другими словами, если δ>0 и |Θ — Θ*| < δ, то чем меньше δ, тем оценка точнее. Таким образом, положительное число δ характеризует точность оценки.
Однако статистические методы не позволяют категорически утверждать, что оценка Θ* удовлетворяет неравенству |Θ — Θ*| < δ; можно лишь говорить о вероятности γ, с которой это неравенство осуществляется.
Надежностью (доверительной вероятностью) оценки Θ по Θ* называют вероятность γ, с которой осуществляется неравенство |Θ — Θ*| < δ. Обычно надежность оценки задается наперед, причем в качестве γ берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.
Пусть вероятность того, что |Θ — Θ*| < δ, равна γ
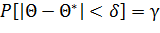 .
.
Заменив неравенство |Θ — Θ*| < δ равносильным ему двойным неравенством -δ<Θ - Θ*<δ, или Θ*-δ< Θ< Θ*+δ, имеем
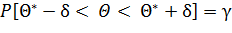 .
.
Это соотношение следует понимать так: вероятность того, что интервал (Θ*-δ, Θ*+δ) заключает в себе (покрывает) неизвестный параметр Θ, равна γ.
Доверительным называют интервал (Θ*-δ, Θ*+δ), который покрывает неизвестный параметр с заданной надежностью γ.
3.2. Доверительные интервалы для оценки математического ожидания нормального распределения при известном σ
Пусть количественный признак Х генеральной совокупности распределен нормально, причем среднее квадратическое отклонение σ этого распределения известно. Требуется оценить неизвестное математическое ожидание α по выборочной средней 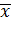 . Поставим своей задачей найти доверительные интервалы, покрывающие параметр α с надежностью γ.
. Поставим своей задачей найти доверительные интервалы, покрывающие параметр α с надежностью γ.
Примем без доказательства, что если случайная величина Х распределена нормально, то выборочная средняя 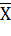 , найденная по независимым наблюдениям, также распределена нормально. Параметры распределения
, найденная по независимым наблюдениям, также распределена нормально. Параметры распределения 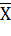 таковы.
таковы.
Потребуем, чтобы выполнялось соотношение
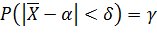 ,
,
где γ— заданная надежность.
Пользуясь формулой
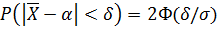 ,
,
заменив Х на 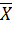 и σ на σ(
и σ на σ(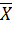 )=
)= 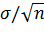 , получим
, получим
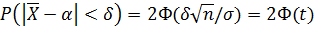 ,
,
где t= 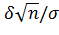 .
.
Найдя из последнего равенства δ= 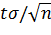 , можем написать
, можем написать
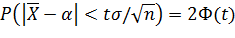 .
.
Приняв во внимание, что вероятность Р задана и равна γ, окончательно имеем (чтобы получить рабочую формулу, выборочную среднюю вновь обозначим через 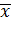 )
)
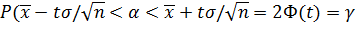 .
.
Смысл полученного соотношения таков: с надежностью γ можно утверждать, что доверительный интервал (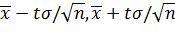 ) покрывает неизвестный параметр α; точность оценки δ=
) покрывает неизвестный параметр α; точность оценки δ= 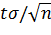 .
.
Итак, поставленная выше задача полностью решена. Укажем еще, что число t определяется из равенства 2Ф(t)=γ, или Ф(t)=γ/2; по таблице функции Лапласа находят аргумент y, которому соответствует значение функции Лапласа, равное γ/2.
Замечаине 1. Оценку 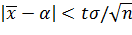 называют классической. Из формулы δ=
называют классической. Из формулы δ= 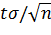 , определяющей точность классической оценки, можно сделать следующие выводы:
, определяющей точность классической оценки, можно сделать следующие выводы:
1) при возрастании объема выборки n число δ убывает и, следовательно, точность оценки увеличивается;
2) увеличение надежности оценки γ=2Ф(t) приводит к увеличению t(Ф(t) — возрастающая функция), следовательно, и к возрастанию δ; другими словами, увеличение надёжности классической оценки влечет за собой уменьшение ее точности.
M(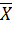 )=α, σ(
)=α, σ(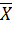 )=
)= 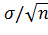 .
.
Поясним смысл, который имеет заданная надежность. Надежность γ=0,95 указывает, что если произведено достаточно большое число выборок, то 95% из них определяет такие доверительные интервалы, в которых параметр действительно заключен; лишь в 5% случаев он может выйти за границы доверительного интервала.
Замечание 2. Если требуется оценить математическое ожидание с наперед заданной точностью δ н надежностью γ, то минимальный объем выборки, который обеспечит эту точность, находят по формуле
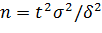
(следствие равенства δ= 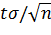 .).
.).
3.3. Доверительные интервалы для оценки математического ожидания нормального распределения при неизвестном σ
Пусть количественный признак Х генеральной совокупности распределен нормально, причем среднее квадратическое отклонение σ неизвестно. Требуется оценить неизвестное математическое ожидание α с помощью доверительных интервалов. Разумеется, невозможно воспользоваться результатами предыдущего параграфа, в котором σ предполагалось известным.
Оказывается, что по данным выборки можно построить случайную величину (ее возможные значения будем обозначать через t):
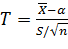 ,
,
которая имеет распределение Стьюдента с k=n-1 степенями свободы (см. пояснение в конце параграфа); здесь 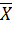 — выборочная средняя, S —«исправленное» среднее квадратическое отклонение, n — объем выборки.
— выборочная средняя, S —«исправленное» среднее квадратическое отклонение, n — объем выборки.
Плотность распределения Стьюдента
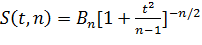 ,
,
Где 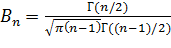 .
.
Распределение Стьюдента определяется параметром n — объемом выборки (или, что то же, числом степеней свободы k=n-1) и не зависит от неизвестных параметров α и σ; эта особенность является его большим достоинством. Поскольку S(t, n) — четная функция от t, вероятность осуществления неравенства 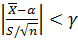 определяется так:
определяется так:
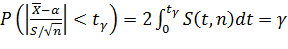 .
.
Заменив неравенство в круглых скобках равносильнымему двойным неравенством, получим
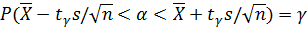 .
.
Итак, пользуясь распределением Стьюдента, мы нашли доверительный интервал (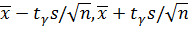 ), покрывающий неизвестный параметр α с надежностью γ. Здесь случайные величины
), покрывающий неизвестный параметр α с надежностью γ. Здесь случайные величины 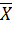 и S заменены неслучайными величинами
и S заменены неслучайными величинами 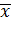 и s, найденными по выборке. По таблице приложения 3 по заданным n и γ можно найти tγ.
и s, найденными по выборке. По таблице приложения 3 по заданным n и γ можно найти tγ.
Замечание. Из предельных соотношений
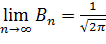 ,
, 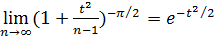 ,
,
следует, что при неограниченном возрастании объема выборки n распределение Стьюдеита стремится к нормальному. Поэтому практически при n > 30 можно вместо распределения Стьюдента пользоваться нормальным распределением.
Однако важно подчеркнуть, что для малых выборок (n < 30), в особенности для малых значений n, замена распределения нормальным приводит к грубым ошибкам, а именно к неоправданному сужению доверительного интервала, т. е. к повышению точности оценки. Например, если n=5 и γ= 0,99, то, пользуясь распределением Стьюдента, найдем tγ=4,6, а используя функцию Лапласа, найдем tγ = 2,58, т. е. доверительный интервал в последнем случае окажется более узким, чем найденный по распределению Стьюдента.
4. Оценка истинного значения измеряемой величины
Пусть производится n независимых равноточных измерений некоторой физической величины, истинное значение α которой неизвестно. Будем рассматривать результаты отдельных измерений как случайные величины
Х1, X2,..., Xn. Эти величины независимы (измерения независимы), имеют одно и то же математическое ожидание α (истинное значение измеряемой величины), одинаковые дисперсии σ2 (измерения равноточны) и распределены нормально (такое допущение подтверждается опытом).
Таким образом, все предположения, которые были сделаны при выводе доверительных интервалов в двух предыдущих параграфах, выполняются, и, следовательно, можно использовать полученные в них формулы.
Другими словами, истинное значение измеряемой величины можно оценивать по среднему арифметическому результатов отдельных измерений при помощи доверительных интервалов. Поскольку обычно σ неизвестно.
4.1. Доверительные интервалы для оценки среднего квадратического отклонения σ нормального распределения
Пусть количественный признак Х генеральной совокупности распределен нормально. Требуется оценить неизвестное генеральное среднее квадратическое отклонение с по «исправленному» выборочному среднему квадратическому отклонению s. Поставим перед собой задачу найти доверительные интервалы, покрывающие параметр σ с заданной надежностью γ.
Потребуем, чтобы выполнялось соотношение
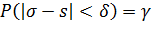 , или
, или 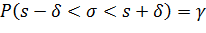 .
.
Для того чтобы можно было пользоваться готовой таблицей, преобразуем двойное неравенство
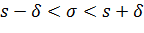
в равносильное неравенство
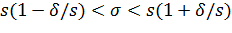 .
.
Положив δ/s=q, получим
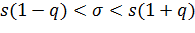 . (*)
. (*)
Остается найти q. С этой целью введем в рассмотрение
случайную величину «хи»:
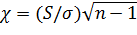 ,
,
где n— объем выборки.
Величина 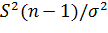 распределена по закону χ2 с n—1 степенями свободы, поэтому квадратный корень из нее обозначают через χ.
распределена по закону χ2 с n—1 степенями свободы, поэтому квадратный корень из нее обозначают через χ.
Плотность распределения у имеет вид (см. пояснение в конце параграфа)
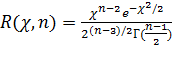 . (**)
. (**)
Это распределение не зависит от оцениваемого параметра σ, а зависит лишь от объема выборки n.
Преобразуем неравенство (*) так, чтобы оно приняло вид χ1<χ<χ2. Вероятность этого неравенства равна заданной вероятности γ, т.е.
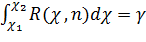 .
.
Предполагая, что q < 1, перепишем неравенство (*) так:
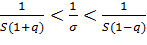 ,
,
Умножив все члены неравенства на 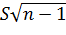 , получим
, получим
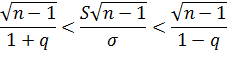
или
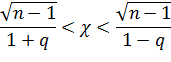
Вероятность того, что это неравенство, а следовательно, и равносильное ему неравенство (*) будет осуществлено, равна
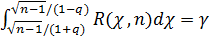 .
.
Из этого уравнения можно по заданным n и γ найти q. Практически для отыскания q пользуются таблицей приложения 4.
Вычислив по выборке s и найдя по таблице q, получим искомый доверительный интервал (*), покрывающий σ с заданной надежностью γ, т.е. интервал
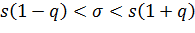 .
.
4.2. Оценка вероятности (биномиального распределения) по относительной частоте
Пусть производятся независимые испытания с неизвестной вероятностью p появления события А в каждом испытании.
Требуется оценить неизвестную вероятность р по относительной частоте, т.е. надо найти ее точечную и интервальную оценки.
А. Точечная оценка. В качестве точечной оценки неизвестной вероятности р принимают относительную частоту
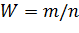 ,
,
где m—число появлений события А; n—число испытаний *.
Эта оценка несмещенная, т.е. ее математическое ожидание равно оцениваемой вероятности. Действительно, учитывая, что M(m)=np, получим
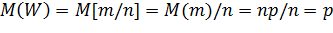 .
.
Найдем дисперсию оценки, приняв во внимание, что D(m)=npq:
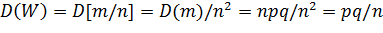 .
.
Отсюда среднее квадратическое отклонение,
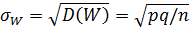 .
.
Б. Интервальная оценка. Найдем доверительный интервал для оценки вероятности по относительной частоте. Ранее была выведена формула, позволяющая найти вероятность того, что абсолютная величина отклонения не превысит положительного числа δ:
P(|X - α| < δ) = 2Ф(δ/σ), (*)
где Х —нормальная случайная величина с математическим ожиданием М(Х)=α.
Если n достаточно велико и вероятность р не очень близка к нулю и к единице, то можно считать, что относительная частота распределена приближенно нормально, причем, как показано в п. А, М(W)=р.
Таким образом, заменив в соотношении (*) случайную величину Х и ее математическое ожидание α соответственно случайной величиной W и ее математическим ожиданием р, получим приближенное (так как относительная частота распределена приближенно нормально) равенство
P(|X - p| < δ) = 2Ф(δ/σW). (**)
Приступим к построению доверительного интервала (p1, p2), который с надежностью у покрывает оцениваемый параметр р, для чего используем рассуждения, с помощью которых был построен доверительный интервал. Потребуем, чтобы с надежностью γ выполнялось соотношение (**):
P(|X - p| < δ) = 2Ф(δ/σ) = γ.
Заменив σW через 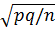 , получим
, получим
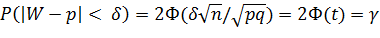 ,
,
где t= 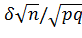 .
.
Отсюда
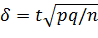
и, следовательно,
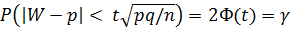 .
.
Таким образом, с надежностью γ выполняется неравенство (чтобы получить рабочую формулу, случайную величину W заменим неслучайной наблюдаемой относительной частотой w и подставим 1 - p вместо q):
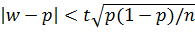 .
.
Учитывая, что вероятность р неизвестна, решим это неравенство относительно р. Допустим, что w > р. Тогда
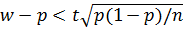 .
.
Обе части неравенства положительны; возведя их в квадрат, получим равносильное квадратное неравенство относительно р:
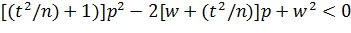 .
.
Дискриминант трехчлена положительный, поэтому его корни действительные и различные:
меньший корень
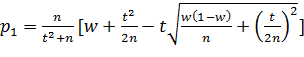 . (***)
. (***)
больший корень
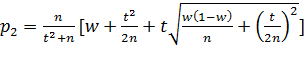 . (****)
. (****)
Итак, искомый доверительный интервал p1 < p < p2,
где р1 и р2 находят по формулам (***) и (****).
При выводе предполагалось, что w > р; тот же результат получится при w < р.
Замечание 1. При больших значениях n (порядка сотен) слагаемые t2/(2n) и (t2/(2n))2 очень малы и множитель n/(t2+n) ≈1,
поэтому можно принять в качестве приближенных границ доверительного интервала
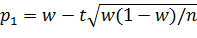 и
и 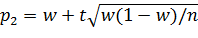
5. Метод моментов для точечной оценки параметров распределения
Начальные и центральные эмпирические моменты являются состоятельными оценками соответственно начальных и центральных теоретических моментов того же порядка. На этом основан метод моментов, предложенный К. Пирсоном. Достоинство метода — сравнительная его простота. Метод моментов точечной оценки неизвестных параметров заданного распределения состоит в приравнивании теоретических моментов рассматриваемого распределения соответствующим эмпирическим моментам того же порядка.
А. Оценка одного параметра. Пусть задан вид плотности распределения f(x, θ), определяемой одним неизвестным параметром θ. Требуется найти точечную оценку параметра θ.
Для оценки одного параметра достаточно иметь одно уравнение относительно этого параметра. Следуя методу моментов, приравняем, например, начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка: ν1. Учитывая, что ν1 = М(Х), М1 = 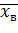 , получим
, получим
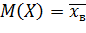 (*)
(*)
Математическое ожидание М(Х), как видно из соотношения
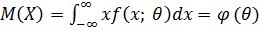 ,
,
есть функция от θ, поэтому (*) можно рассматривать как уравнение с одним неизвестным θ. Решив это уравнение относительно параметра 0, можно найти его точечную оценку θ*, которая является функцией от выборочной средней, следовательно, и от вариант выборки:
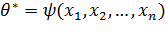 .
.
Б. Оценка двух параметров. Пусть задан вид плотности распределения f(x; θ1; θ2), определяемой неизвестными параметрами θ1 и θ2,. Для отыскания двух параметров необходимы два уравнения относительно этих параметров. Следуя методу моментов, приравняем, например, начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка и центральный теоретический момент второго порядка центральному эмпирическому моменту второго порядка:
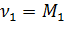 ,
, 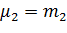 .
.
Учитывая, что ν1 = М(Х), μ2 =D(Х), М1= 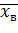 , m2=Dв, получим
, m2=Dв, получим
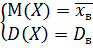 (**)
(**)
Математическое ожидание и дисперсия есть функции от θ1, н θ2, поэтому (**) можно рассматривать как систему двух уравнений с двумя неизвестными θ1, н θ2. Решив эту систему относительно неизвестных параметров, тем самым получим их точечные оценки 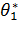 и
и 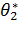 . Эти оценки являются функциями от вариант выборки:
. Эти оценки являются функциями от вариант выборки:
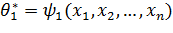 ,
,
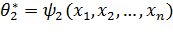 ,
,
5.1. Метод наибольшего правдоподобия
Кроме метода моментов существуют и другие методы точечной оценки неизвестных параметров распределения. К ним относится метод наибольшего правдоподобия, предложенный Р. Фишером.
А. Дискретные случайные величины. Пусть Х — дискретная случайная величина, которая в результате п испытаний приняла значения x1, х2,..., xn. Допустим, что вид закона распределения величины Х задан, но неизвестен параметр θ, которым определяется этот закон. Требуется найти его точечную оценку.
Обозначим вероятность того, что в результате испытания величина Х примет значение хi(i=1, 2,..., n), через р(хi; θ).
Функцией правдоподобия дискретной случайной велицчины Х называют функцию аргумента θ:
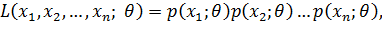
где 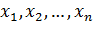 – фиксированные числа.
– фиксированные числа.
В качестве точечной оценки параметра 9 принимают такое его значение θ* = θ*(х1, х2,..., хn), при котором функция правдоподобия достигает максимума. Оценку θ* называют оценкой наибольшего правдоподобия.
Функции L и lnL, достигают максимума при одном и том же значении θ, поэтому вместо отыскания максимума функции L, ищут (что удобнее) максимум функции lnL.
Логарифмической функцией правдоподобия называют функцию lnL. Как известно, точку максимума функции lnL аргумента θ можно искать, например, так:
1) найти производную — 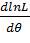 ;
;
2) приравнять производную нулю и найти критическую точку — корень полученного уравнения (его называют уравнением правдоподобия);
3) найти вторую производную 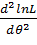 ; если вторая производная при θ = θ* отрицательна, то θ* —точка максимума.
; если вторая производная при θ = θ* отрицательна, то θ* —точка максимума.
Найденную точку максимума θ* принимают в качестве оценки наибольшего правдоподобия параметра 0.
Метод наибольшего правдоподобия имеет ряд достоинств: оценки наибольшего правдоподобия состоятельны (но они могут быть смещенными), распределены асимптотически нормально (при больших значениях n приближенно нормальны) и имеют наименьшую дисперсию по сравнению с другими асимптотически нормальными оценками; если для оцениваемого параметра θ существует эффективная оценка θ*, то уравнение правдоподобия имеет единственное решение θ*; этот метод наиболее полно использует данные выборки об оцениваемом параметре, поэтому он особенно полезен в случае малых выборок.
Недостаток метода состоит в том, что он часто требует сложных вычислений.
Замечание 1. Функция правдоподобия — функция от аргумента θ; оценка наибольшего правдоподобие— функция от независимых аргументов x1, x2,…, xn.
Замечание 2. Оценка наибольшего правдоподобия не всегда совпадает с оценкой, найденной методом моментов..
Б. Непрерывные случайные величины. Пусть Х — непрерывная случайная величина, которая в результате n испытаний приняла значения х1, х2,..., хn. Допустим, что вид плотности распределения f(х) задан, но не известен параметр θ, которым определяется эта функция.
Функцией правдоподобия непрерывной случайной величины Х называют функцию аргумента θ:
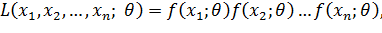
где 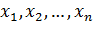 – фиксированные числа.
– фиксированные числа.
Оценку наибольшего правдоподобия неизвестного параметра распределения непрерывной случайной величины ищут так же, как в случае дискретной величины.
Замечание. Если плотность распределения f(х) непрерывной случайной величины Х определяется двумя неизвестными параметрами θ1 н θ2, то функция правдоподобия является функцией двух независимых аргументов θ1 н θ2:
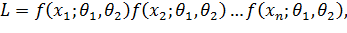
где 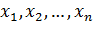 —наблюдавшиеся значения Х. Далее находят логарифмическую функцию правдоподобия и для отыскания ее максимума составляют н решают систему
—наблюдавшиеся значения Х. Далее находят логарифмическую функцию правдоподобия и для отыскания ее максимума составляют н решают систему
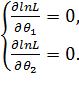
5.2. Другие характеристики вариационного ряда
Кроме выборочной средней и выборочной дисперсии применяются и другие характеристики вариационного ряда.
Модой Мo, называют варианту, которая имеет наибольшую частоту. Например, для ряда
варианта.... 1 4 7 9
частота.... 5 1 20 6
мода равна 7.
Медианой me. называют варианту, которая делит вариационный ряд на две час
|
|
 2020-04-20
2020-04-20 138
138