Пусть функция 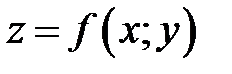 непрерывна в ограниченной замкнутой области
непрерывна в ограниченной замкнутой области 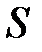 на плоскости
на плоскости 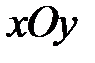 . Разобьем область
. Разобьем область 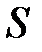 произвольным образом на
произвольным образом на  элементарных областей, имеющих площади
элементарных областей, имеющих площади 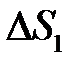 ,
, 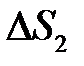 , …,
, …, 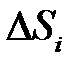 , …,
, …, 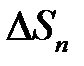 . Выберем в каждой элементарной области точку
. Выберем в каждой элементарной области точку 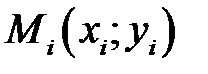 и умножим значение функции в этой точке на площадь области
и умножим значение функции в этой точке на площадь области 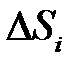 . Двумерной интегральной суммой для функции
. Двумерной интегральной суммой для функции 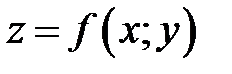 по области
по области 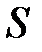 называется сумма вида
называется сумма вида
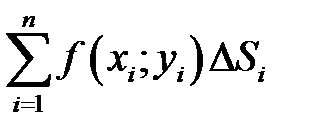 . Двойным интегралом от функции
. Двойным интегралом от функции 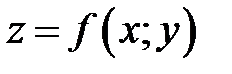 по области
по области 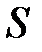 называется предел последовательности двумерных интегральных сумм, если он существует и не зависит от способа разбиения области
называется предел последовательности двумерных интегральных сумм, если он существует и не зависит от способа разбиения области 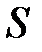 на части и выбора точек
на части и выбора точек 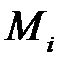 . Обозначается
. Обозначается 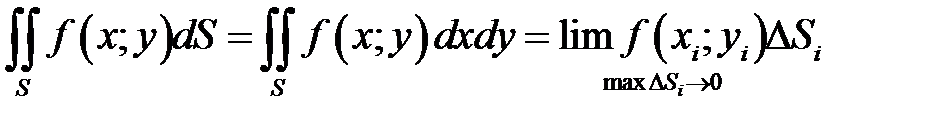
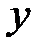
|
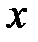
|
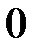
|
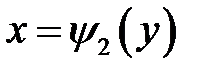
|
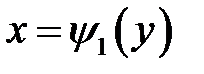
|
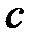
|
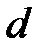
|
 в области
в области 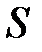 , то двойной интеграл равен объему цилиндрического тела, ограниченного сверху поверхностью
, то двойной интеграл равен объему цилиндрического тела, ограниченного сверху поверхностью 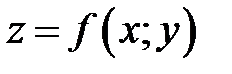 , сбоку цилиндрической поверхностью с образующими, параллельными оси
, сбоку цилиндрической поверхностью с образующими, параллельными оси 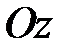 , снизу областью
, снизу областью 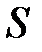 плоскости
плоскости 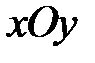 . Площадь области
. Площадь области 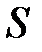 равна
равна 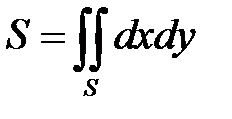 .
.
Рисунок 4.1 – область 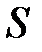 : : 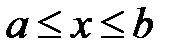 и и 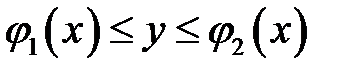
|
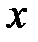
|
|
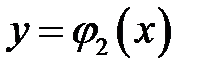
|

|
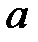
|
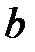
|
Рисунок 4.2 – область 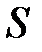 : : 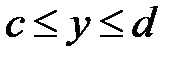 и и 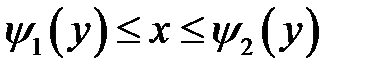
|
Свойства двойного интеграла аналогичны свойствам определенного интеграла. Вычисление двойного интеграла сводится к вычислению двукратного интеграла вида
1) 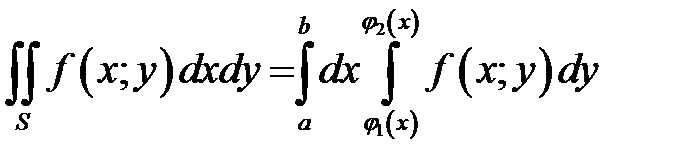 , если область
, если область 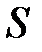 определена условиями:
определена условиями: 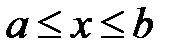 и
и 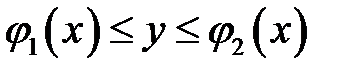 ;
;
2) 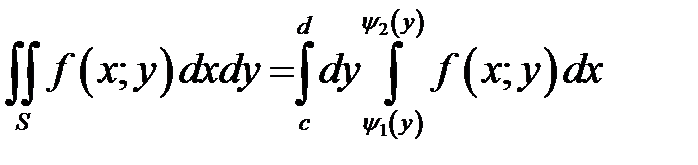 , если область
, если область 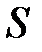 определена условиями:
определена условиями: 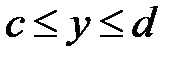 и
и 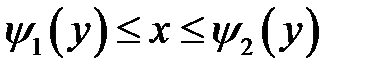 .
.
Переход от первого равенства ко второму или обратно называется изменением порядка интегрирования. Значение двойного интеграла не зависит от порядка интегрирования.
При вычислении двойного интеграла иногда бывает удобно перейти к полярным координатам
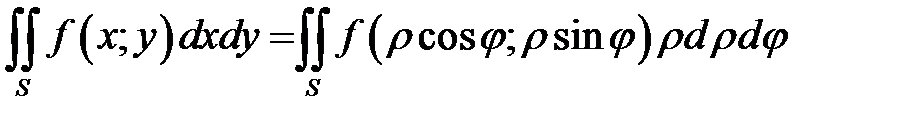 .
.
Тройной интеграл от функции 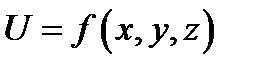 по пространственной области
по пространственной области 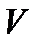 определяется аналогично двойному интегралу
определяется аналогично двойному интегралу
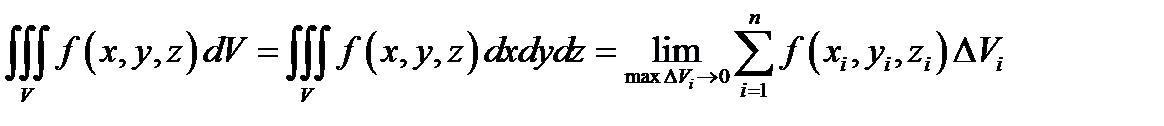
Вычисление тройного интеграла сводится к вычислению трехкратного интеграла вида
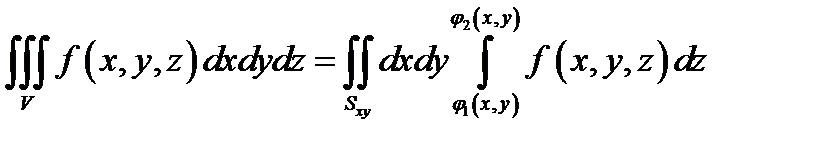 ,
,
где 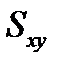 - проекция области
- проекция области 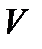 на плоскость
на плоскость 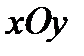 ,
, 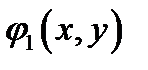 и
и 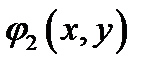 - уравнения поверхностей, ограничивающих область
- уравнения поверхностей, ограничивающих область 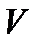 соответственно снизу и сверху.
соответственно снизу и сверху.
Объем тела можно вычислить по формуле
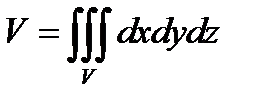 .
.
Пример 1.Изменить порядок интегрирования в двойном интеграле
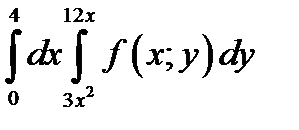 .
.
Решение. Зная пределы интегрирования, определим границы области интегрирования 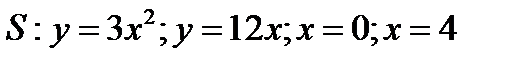 .
.
Построим данную область
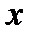
|
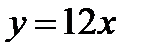
|
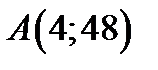
|
|
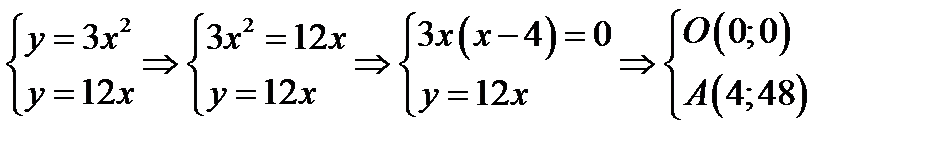 .
.
Рисунок 4.3 – Изображение области 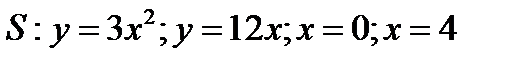
|
 ) и внешнего (по
) и внешнего (по 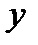 ) интегралов. Слева область ограничена прямой
) интегралов. Слева область ограничена прямой 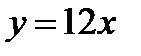 , откуда имеем
, откуда имеем 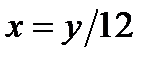 . Справа область ограничена параболой
. Справа область ограничена параболой 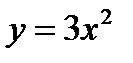 , откуда получим
, откуда получим 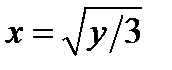 . Наименьшее значение
. Наименьшее значение 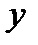 в заданной области равно 0, наибольшее 48. Итак, имеем
в заданной области равно 0, наибольшее 48. Итак, имеем
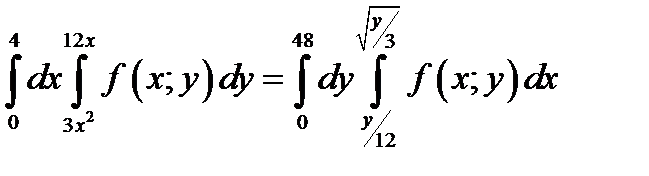 .
.
Пример 2. Изменить порядок интегрирования в двойном интеграле
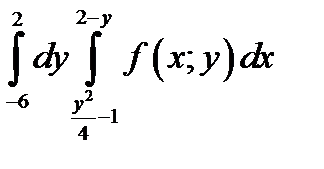 .
.
Решение. Запишем уравнения линий, ограничивающих область, и построим ее 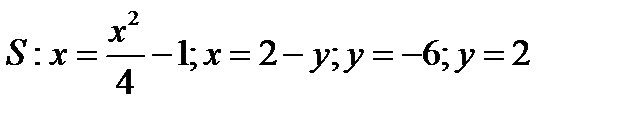 .
.
Рисунок 4.4 – Изображение области 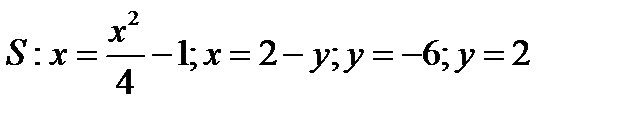
|
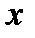
|

|
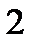
|
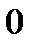
|
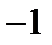
|
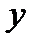
|
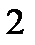
|
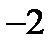
|
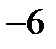
|
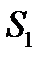
|
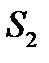
|
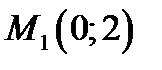
|

|
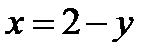
|
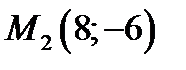
|
Найдем новые пределы внутреннего (по 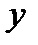 ) и внешнего (по
) и внешнего (по  ) интегралов. Область
) интегралов. Область 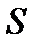 разобьем на две части
разобьем на две части 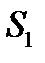 и
и 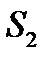 .
.
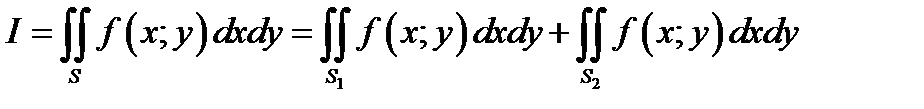 .
.
Область 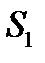 снизу и сверху ограничена ветвями параболы
снизу и сверху ограничена ветвями параболы 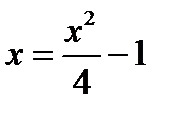 . Уравнения этих ветвей получим, выражая
. Уравнения этих ветвей получим, выражая 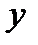 из уравнения параболы
из уравнения параболы 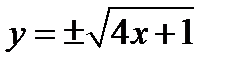 . Наименьшее значение
. Наименьшее значение 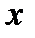 в области
в области 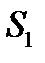 равно (-1), а наибольшее 0.
равно (-1), а наибольшее 0.
Область 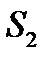 снизу ограничена ветвью параболы
снизу ограничена ветвью параболы 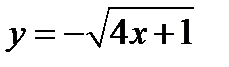 , а сверху прямой
, а сверху прямой 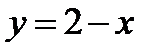 . Наименьшее значение
. Наименьшее значение 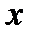 равно 0, наибольшее 8. Таким образом, двойной интеграл с измененным порядком интегрирования запишем в виде
равно 0, наибольшее 8. Таким образом, двойной интеграл с измененным порядком интегрирования запишем в виде
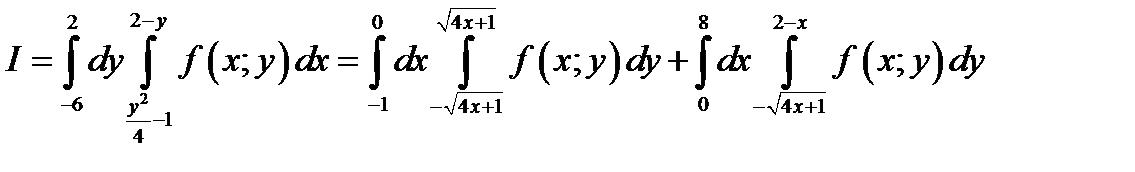
Пример 3. С помощью тройного интеграла вычислить объем тела, ограниченного поверхностями; 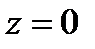 ;
; 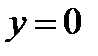 ;
; 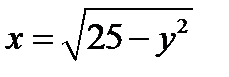 . Сделать схематический чертеж тела и его проекции на плоскость
. Сделать схематический чертеж тела и его проекции на плоскость 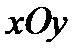 .
.
Рисунок 4.5 – Изображение тела ограниченного поверхностями 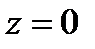 ; ; 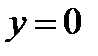 ; ; 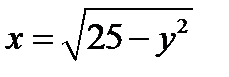 . .
|
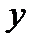
|
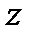
|
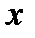
|
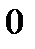
|
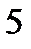
|

|
Рисунок 4.6 – Изображение проекции тела на плоскость 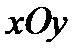
|
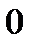
|
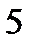
|
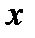
|

|
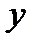
|
Решение. 1) Построим тело. Уравнение  определяет круговой цилиндр с образующей, параллельной оси
определяет круговой цилиндр с образующей, параллельной оси 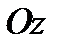 . Уравнение
. Уравнение 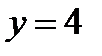 определяет плоскость, параллельную плоскости
определяет плоскость, параллельную плоскости 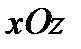 ;
; 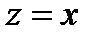 - плоскость, которая делит двугранный угол между плоскостями
- плоскость, которая делит двугранный угол между плоскостями 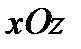 и
и 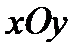 пополам.
пополам.
2) Построим проекцию тела на плоскость 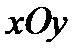 .
.
3) Вычислим объем тела
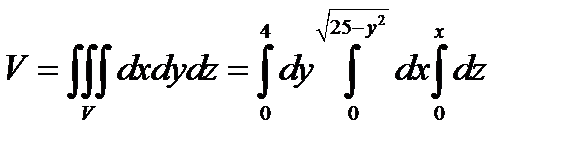 .
.
а) 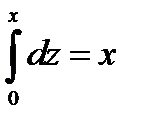 ;
;
б) 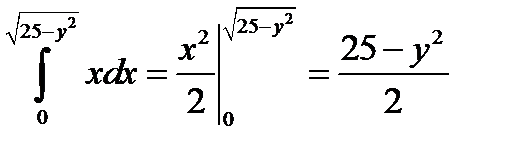 ;
;
в) 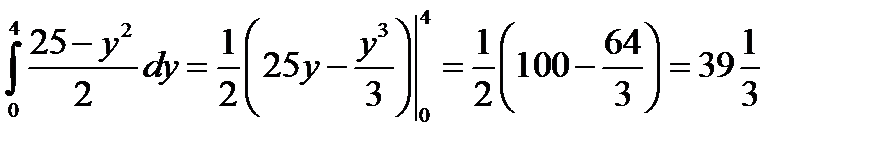 .
.
Объем тела равен 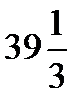 куб.ед.
куб.ед.
Вопросы для самоконтроля.
1. Дайте определение двойного интеграла.
2. Какие геометрические приложения двойного интеграла вы знаете?
3. Как осуществляется переход к полярным координатам при вычислении кратных интегралов?
4. Как изменить порядок интегрирования в двойном интеграле?
Литература: [3] стр. 378-398, [7] стр. 204.
Примеры: [2] стр. 6-23, [9] стр. 230.
Вопросы для подготовки к семестровому контролю
II семестр – зачет с оценкой
- Понятие первообразной функции и неопределенного интеграла.
- Интегрирование методом замены переменной.
- Метод интегрирования по частям.
- Интегрирование рациональных функций. Метод неопределенных коэффициентов.
- Интегрирование тригонометрических функций.
- Интегрирование некоторых рациональных функций.
- Интегрирование некоторых иррациональных функций.
- Понятие и свойства определенного интеграла.
- Формула Ньютона-Лейбница.
- Замена переменной в определенном интеграле.
- Интегралы с бесконечными границами интегрирования.
- Интегралы от разрывных функций.
- Вычисление площадей с помощью определенного интеграла.
- Область интегрирования двойного интеграла. Изменение порядка интегрирования в двойном интеграле.
- Вычисление двойных интегралов в прямоугольной системе координат.
- Двойной интеграл в полярных координатах.
- Геометрические приложения двойного интеграла.
- Физические приложения двойного интеграла.
- Вычисление тройного интеграла в прямоугольной системе координат.
- Вычисление тройного интеграла в цилиндрической и сферической системе координат.
- Геометрические и физические приложения тройного интеграла.
- Криволинейный интеграл II рода. Основные понятия.
- Вычисление криволинейного интеграла II рода.
- Формула Остроградского-Грина. Условия независимости криволинейного интеграла II рода от пути интегрирования.
- Некоторые приложения криволинейного интеграла II рода.
 2020-05-11
2020-05-11 142
142








