Рассмотрим одну из многих задач, положивших начало интегральному исчислению.
Пусть на отрезке  определена непрерывная функция
определена непрерывная функция  и
и  для всех
для всех  (рис.2.1).
(рис.2.1).
| Рисунок 2.1 – Криволинейная трапеция
|
Определение. Фигуру, ограниченную сверху данной кривой

, снизу отрезком оси
Ох с боковыми прямыми

и

, называют криволинейной трапецией. В некоторых случаях

(или

), тогда боковая сторона такой трапеции стягивается в точку.
Найдем площадь этой трапеции. Для этого отрезок  разделим произвольным образом на n частей, точки деления обозначим
разделим произвольным образом на n частей, точки деления обозначим 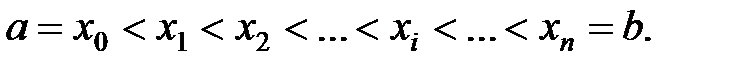 Получили n частичных отрезков
Получили n частичных отрезков  ,
, 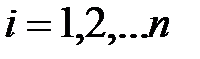 . В каждом i -ом отрезке возьмем произвольную точку
. В каждом i -ом отрезке возьмем произвольную точку  и вычислим значение функции в этой точке
и вычислим значение функции в этой точке  . Длина каждого i -го отрезка будет соответственно равна
. Длина каждого i -го отрезка будет соответственно равна 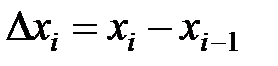 . Произведение
. Произведение 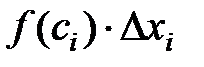 - площадь прямоугольника с основанием
- площадь прямоугольника с основанием  и высотой
и высотой  . Сумма всех таких произведений
. Сумма всех таких произведений  равна площади ступенчатой фигуры и приближенно равна площади S криволинейной трапеции.
равна площади ступенчатой фигуры и приближенно равна площади S криволинейной трапеции.
 .
.
Если теперь в этом выражении начать неограниченно увеличивать число n так, чтобы длинна наибольшего из  , то точность приближенного равенства будет повышаться.
, то точность приближенного равенства будет повышаться.
За точное значение площади криволинейной трапеции принимается предел, к которому стремится площадь ступенчатой фигуры, когда n неограниченно возрастает, так что  :
:  .
.
Сумму  называют интегральной суммой для функции
называют интегральной суммой для функции  на отрезке
на отрезке  .
.
Если отвлечься от геометрического смысла величины S, то предел, с помощью которого вычисляют S, называют определенным интегралом на отрезке  .
.
Определение. Определенным интегралом от функции  на отрезке
на отрезке  называется предел последовательности интегральных сумм, если он существует и не зависит ни от способа разбиения отрезка
называется предел последовательности интегральных сумм, если он существует и не зависит ни от способа разбиения отрезка  на частичные отрезки
на частичные отрезки  , ни от выбора точки
, ни от выбора точки  в них, т.е.
в них, т.е.
 .
.
Функция  называется интегрируемой на[ a;b ];
называется интегрируемой на[ a;b ];  – подынтегральная функция, х – переменная интегрирования; а, b – соответственно нижний и верхний пределы интегрирования.
– подынтегральная функция, х – переменная интегрирования; а, b – соответственно нижний и верхний пределы интегрирования.
Геометрический смысл определенного интеграла: определенный интеграл от неотрицательной функции  численно равен площади соответствующей криволинейной трапеции.
численно равен площади соответствующей криволинейной трапеции.
 определена непрерывная функция
определена непрерывная функция  и
и  для всех
для всех  (рис.2.1).
(рис.2.1). , снизу отрезком оси Ох с боковыми прямыми
, снизу отрезком оси Ох с боковыми прямыми  и
и  , называют криволинейной трапецией. В некоторых случаях
, называют криволинейной трапецией. В некоторых случаях  (или
(или  ), тогда боковая сторона такой трапеции стягивается в точку.
), тогда боковая сторона такой трапеции стягивается в точку.
 разделим произвольным образом на n частей, точки деления обозначим
разделим произвольным образом на n частей, точки деления обозначим 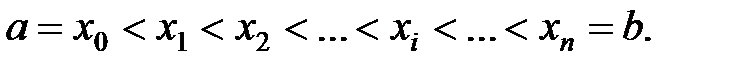 Получили n частичных отрезков
Получили n частичных отрезков  ,
, 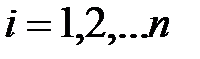 . В каждом i -ом отрезке возьмем произвольную точку
. В каждом i -ом отрезке возьмем произвольную точку  и вычислим значение функции в этой точке
и вычислим значение функции в этой точке  . Длина каждого i -го отрезка будет соответственно равна
. Длина каждого i -го отрезка будет соответственно равна 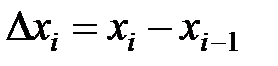 . Произведение
. Произведение 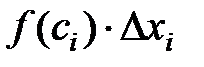 - площадь прямоугольника с основанием
- площадь прямоугольника с основанием  и высотой
и высотой  . Сумма всех таких произведений
. Сумма всех таких произведений  равна площади ступенчатой фигуры и приближенно равна площади S криволинейной трапеции.
равна площади ступенчатой фигуры и приближенно равна площади S криволинейной трапеции. .
. , то точность приближенного равенства будет повышаться.
, то точность приближенного равенства будет повышаться. :
:  .
. называют интегральной суммой для функции
называют интегральной суммой для функции  на отрезке
на отрезке  .
. .
. на отрезке
на отрезке  называется предел последовательности интегральных сумм, если он существует и не зависит ни от способа разбиения отрезка
называется предел последовательности интегральных сумм, если он существует и не зависит ни от способа разбиения отрезка  на частичные отрезки
на частичные отрезки  , ни от выбора точки
, ни от выбора точки  в них, т.е.
в них, т.е. .
. называется интегрируемой на[ a;b ];
называется интегрируемой на[ a;b ];  – подынтегральная функция, х – переменная интегрирования; а, b – соответственно нижний и верхний пределы интегрирования.
– подынтегральная функция, х – переменная интегрирования; а, b – соответственно нижний и верхний пределы интегрирования. численно равен площади соответствующей криволинейной трапеции.
численно равен площади соответствующей криволинейной трапеции. 2020-05-11
2020-05-11 92
92








