Особенности расчёта режимов местных электрических сетей (35 кВ и ниже)

при расчёте режимов местных сетей принебрегают ёмкостной проводимостью линии;

Считают при расчёте потерь мощности и напряжения на участках сети U = U_н во всех точках сети;

В местных сетях принебрегают поперечной составляющей напряжения и считают, что потери напряжения приблизительно равны продольной составляющей падения напряжения.

сеть без потерь.

(P₁+P₂)-j(q₁+q₂)

а) один участок сети (рис. 6.14.)

Û_нI;	(6.34.)
Û_нI;	(6.35.)

б) два участка сети (рис. 6.15.)

Рис. 6.15.

(6.36.)

расчёт сети с учётом потерь мощности и напряжения (рис. 6.16.)

Цель: определить ∆P_∑, ∆Q_∑, ∆U_0-2.

Рис. 6.16.

∆P_∑ = ;	(6.37.)
∆Q_∑ = ;	(6.38.)
∆U_0-2 = ;	(6.39.)

I_a

Так как:

Р₂=

Q₂=

(6.40.)

Рис. 6.17.

С учётом выражения (6.41.) получаем:

∆U_0-2 =

;

(6.42.)

для электрической сети, состоящей из “n” элементов, имеем:

∆U_on = ;	(6.43.)
∆U_on = ;	(6.44.)
∆U_on = 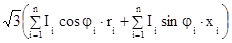;	(6.45.)

В формулах (6.43. ¸6.45.) – P, Q, I – потоки мощности и токи по участкам сети.

3) расчёт потери напряжения в местной сети без учёта потерь мощности (рис. 6.18.)

Цель: Определить потери напряжения, если известны мощности нагрузок по участкам, сопротивление линии и задано номинальное напряжение. P₁, Q₁, P₂, Q₂ – мощности на участках сети.

p₂-q₂

p₁ –q₁

Рис. 6.18.

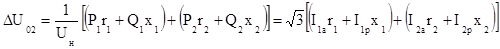;	(6.46.)
P₁=p₁+p₂; P₂=p₂ Q₁=q₁+q₂; Q₂=q₂	(6.47.)
;	(6.48.)

С учётом обозначений на рис. 6.19., выражение (6.48.) для сети, состоящей из “n” участков примет вид:

;	(6.49.)
;	(6.50.)

где:

R₁ и X₁ – сопротивления от начала до конца участка

Если нагрузка задана в токах, то потери напряжения рассчитываются по формуле (6.50.).

При расчёте режимов кабельных сетей обычно пренебрегают реактивным сопротивлением (Х). Соответственно во всех формулах для расчёта исчезают составляющие: q_ix_i и i_pix_i.