Параграф 1. Разложение аналитической в круге функции в ряд Тейлора.
Квант. 07.01.01. Теорема о разложении аналитической в круге функции в ряд Тейлора (Т)
 Рассмотрим функцию комплексного переменного
Рассмотрим функцию комплексного переменного 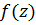
 Пусть функция
Пусть функция 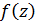 аналитична в круге
аналитична в круге 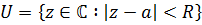
 Тогда функция
Тогда функция 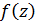 разлагается в нем в степенной ряд Тейлора
разлагается в нем в степенной ряд Тейлора
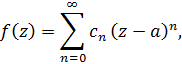
коэффициенты которого определяются по формулам
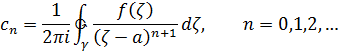
где 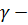 замкнутый контур, лежащий в круге
замкнутый контур, лежащий в круге 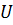 и содержащий внутри себя точку
и содержащий внутри себя точку 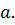
Доказательство.
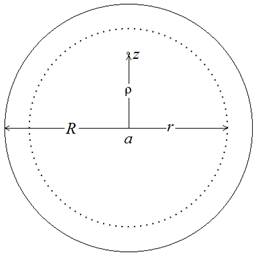
Пусть функция 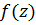 аналитична в круге
аналитична в круге 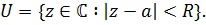 Возьмем произвольную точку
Возьмем произвольную точку 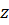 из этого круга и обозначим
из этого круга и обозначим 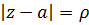 , выберем число
, выберем число 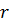 , удовлетворяющее условию
, удовлетворяющее условию 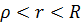 . Возьмем окружность
. Возьмем окружность 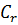 с центром в точке
с центром в точке 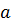 радиуса
радиуса 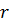 (см. рис.) и напишем формулу Коши
(см. рис.) и напишем формулу Коши
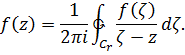
Разложим ядро Коши в степенной ряд, используя формулу суммы геометрической прогрессии.
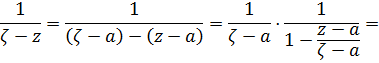
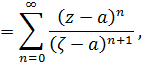
поскольку
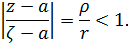
Полученный степенной ряд сходится равномерно на окружности 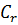 и его равномерная сходимость не нарушится после умножения его на ограниченную (что следует из ее непрерывности) функцию
и его равномерная сходимость не нарушится после умножения его на ограниченную (что следует из ее непрерывности) функцию 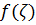 . Интегрируя ряд почленно, получим
. Интегрируя ряд почленно, получим
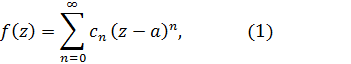
где
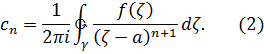
В этой формуле мы заменили контур интегрирования 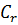 на произвольный замкнутый кусочно-гладкий контур
на произвольный замкнутый кусочно-гладкий контур 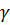 , лежащий в круге
, лежащий в круге 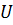 и содержащий внутри себя точку
и содержащий внутри себя точку 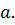 Это возможно в силу теоремы Коши для многосвязной области.
Это возможно в силу теоремы Коши для многосвязной области.
По формуле Коши для производных аналитической функции из предыдущей лекции мы имеем
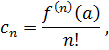
так что ряд (1) является рядом Тейлора для функции 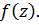
Замечание (оценка коэффициентов ряда Тейлора).
Положим
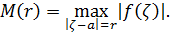
Из формулы (2) имеем
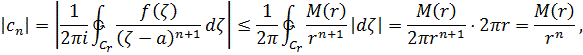
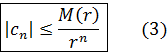
Квант. 07.01.02. Теорема Лиувилля (Т)
 Рассмотрим функцию комплексного переменного
Рассмотрим функцию комплексного переменного 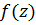 аналитическую во всей комплексной плоскости
аналитическую во всей комплексной плоскости 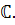



 Пусть функция
Пусть функция 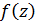 ограничена по модулю
ограничена по модулю
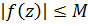
 Тогда функция
Тогда функция 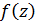 - константа,
- константа, 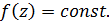
Доказательство.
Пусть 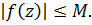 Из формулы (3) имеем
Из формулы (3) имеем
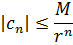
для любого 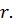 Устремляя
Устремляя 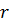 к бесконечности, получим
к бесконечности, получим
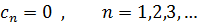
и 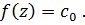 Теорема доказана.
Теорема доказана.
Математические примеры и задачи.
Используя разложения основных элементарных функций, а также возможность почленного дифференцирования и интегрирования степенных рядов, разложить функции в ряд по степеням 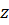 и указать области сходимости полученных рядов.
и указать области сходимости полученных рядов.
1.
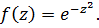
Решение.
Используя разложение показательной функции, справедливое во всей комплексной плоскости, получим
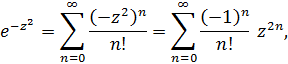
область сходимости
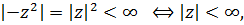
то есть вся комплексная плоскость 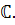
2.
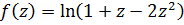
Решение.
Используя разложение главной ветви логарифма, получим
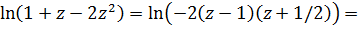
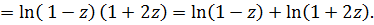
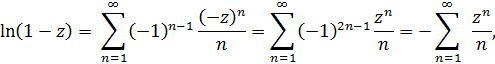
разложение справедливо, если 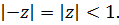
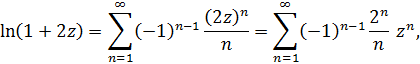
разложение справедливо, если 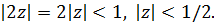
Складывая разложения для 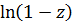 и
и 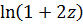 ( складывая коэффициенты при одинаковых степенях
( складывая коэффициенты при одинаковых степенях 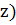 и беря пересечение областей, в которых они справедливы, получим
и беря пересечение областей, в которых они справедливы, получим
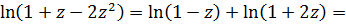
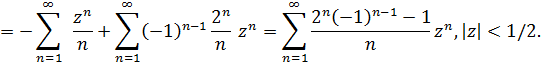
3.
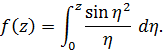
Решение.
Используя разложение синуса справедливое во всей комплексной плоскости и почленное интегрирование степенного ряда, получим
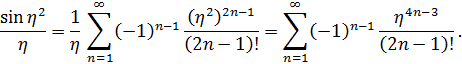
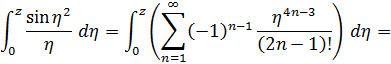
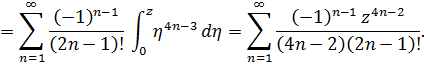
Это разложение справедливо во всей комплексной плоскости, поскольку при интегрировании степенного ряда его радиус сходимости не меняется.
 2020-05-12
2020-05-12 117
117







