Квант. 07.02.01. Теорема о разложении аналитической в кольце функции в ряд Лорана (Т)
 Рассмотрим функцию комплексного переменного
Рассмотрим функцию комплексного переменного 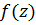
 Пусть функция
Пусть функция 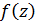 аналитична в кольце
аналитична в кольце
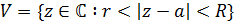
 Тогда функция
Тогда функция 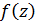 разлагается в нем в степенной ряд Лорана
разлагается в нем в степенной ряд Лорана
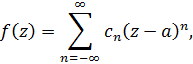
коэффициенты которого определяются по формулам
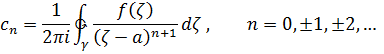
где 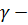 замкнутый контур, лежащий в кольце
замкнутый контур, лежащий в кольце 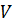 и содержащий внутри себя точку
и содержащий внутри себя точку 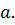
Доказательство.
 Пусть функция
Пусть функция 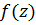 аналитична в кольце
аналитична в кольце
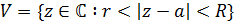
и 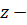 произвольная точка из этого кольца. Обозначим
произвольная точка из этого кольца. Обозначим 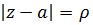 и выберем числа
и выберем числа 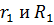 так, чтобы выполнялись неравенства
так, чтобы выполнялись неравенства
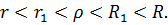
Обозначим 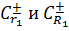 окружности с центром в точке
окружности с центром в точке 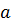 радиусов
радиусов  соответственно
соответственно
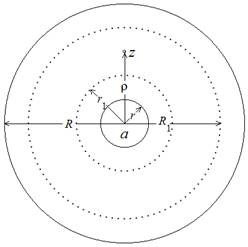
(см. рис.). Знаки плюс и минус указывают направление обхода, плюс – против часовой стрелки, минус – по часовой стрелке. Запишем формулу Коши для двухсвязной области
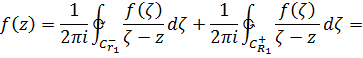
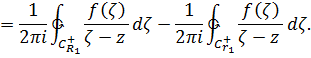
Разложим ядра Коши в ряды, используя формулу суммы геометрической прогрессии, а затем проинтегрируем почленно. Имеем на окружности 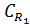
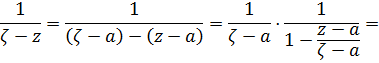
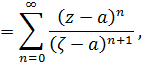
поскольку

На окружности 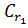 имеем
имеем
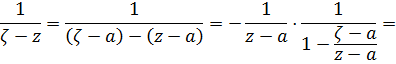
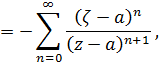
поскольку
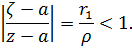
Интегрируя почленно, получаем
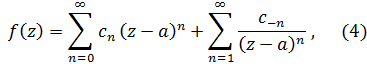
где
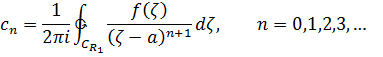
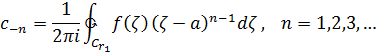
Вторую формулу можно переписать так
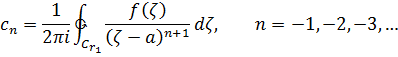
В силу теоремы Коши для многосвязной области мы можем заменить контуры интегрирования 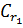 и
и 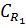 на произвольный замкнутый кусочно-гладкий контур
на произвольный замкнутый кусочно-гладкий контур 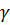 , лежащий в кольце
, лежащий в кольце 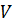 и содержащий внутри себя точку
и содержащий внутри себя точку 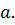
Ряд Лорана можно записать так
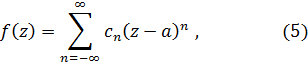
где
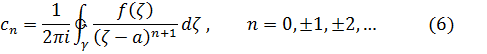
Замечание.
Ряд (4) называется рядом Лорана при этом ряд
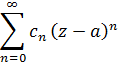
называется правильной частью, а ряд
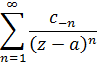
называется главной частью разложения Лорана.
Математические примеры и задачи.
Записать все возможные разложения по степеням 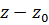 заданных функций и указать области сходимости полученных рядов.
заданных функций и указать области сходимости полученных рядов.
1.
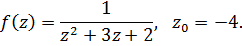
Решение.
Найдем нули знаменателя,

Следовательно, функция аналитична в следующих областях с центром в точке 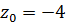 и не содержащих точек
и не содержащих точек 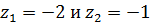 :
:
I) круг 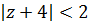 ,
,
II) кольцо 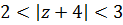 ,
,
III) кольцо 3 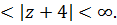
В области I функция разлагается в ряд Тейлора, а в областях II и III в ряд Лорана. Чтобы получить эти разложения, разложим нашу дробно-рациональную функцию на сумму простейших дробей и каждую из этих дробей приведем к виду суммы сходящейся геометрической прогрессии.
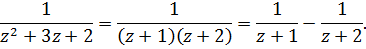
I)

Это сумма сходящейся геометрической прогрессии, поскольку
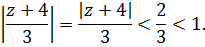
Следовательно
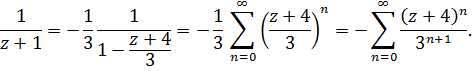
Аналогично

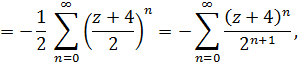
поскольку
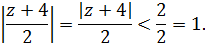
И наша функция разлагается в ряд Тейлора
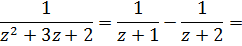

II) Для первой дроби разложение сохранится
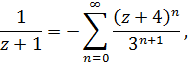
так как
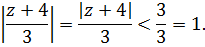
Для второй дроби разложение изменится.

Это сумма сходящейся геометрической прогрессии, так как
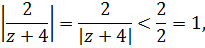
поэтому
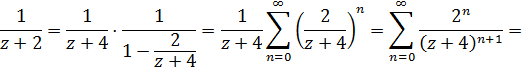
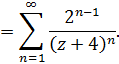
И наша функция разлагается в ряд Лорана
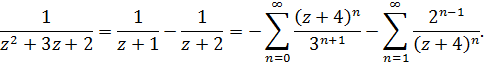
Здесь правильная часть разложения Лорана-
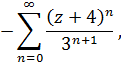
главная часть –
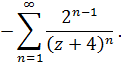
III) Для второй дроби разложение такое же, как в предыдущем случае
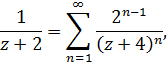
так как
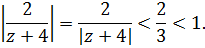
Для первой дроби разложение изменится

Это сумма сходящейся геометрической прогрессии, так как

поэтому
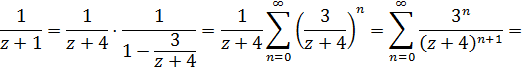
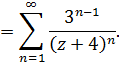
И наша функция разлагается в ряд Лорана

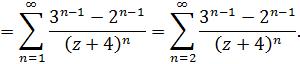
Разложение Лорана состоит только из главной части, правильная часть отсутствует.
2.
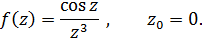
Решение.
Используя разложение косинуса, получим в кольце
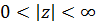
разложение заданной функции в ряд Лорана


Здесь правильная часть разложения Лорана-
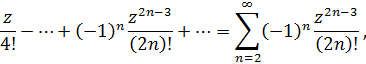
главная часть –
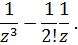
 2020-05-12
2020-05-12 159
159







