Пусть функция 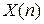 в дискретный момент времени n принимает целое значение i (можно вместо целых чисел i рассматривать любые числа) с вероятностью
в дискретный момент времени n принимает целое значение i (можно вместо целых чисел i рассматривать любые числа) с вероятностью 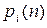 , иначе, некоторая система в момент времени n находится в состоянии i с вероятностью
, иначе, некоторая система в момент времени n находится в состоянии i с вероятностью 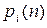 , т. е.
, т. е. 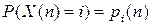 .
.
Совместное распределение вероятностей 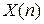 и
и 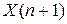 определим формулой
определим формулой  , а совместное распределение случайного вектора
, а совместное распределение случайного вектора 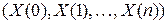 зададим следующим выражением
зададим следующим выражением 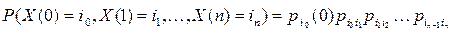 . Таким образом, переход из состояния i в состояние j определяется вероятностью перехода
. Таким образом, переход из состояния i в состояние j определяется вероятностью перехода 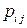 .
.
Определение 1. Последовательность дискретных случайных величин образует марковский процесс, если для каждого набора целых чисел 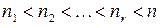 соответствующее совместное распределение
соответствующее совместное распределение 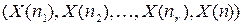 определено таким образом, что условная вероятность события
определено таким образом, что условная вероятность события 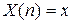 при условиях
при условиях 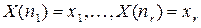 совпадает с условной вероятностью события
совпадает с условной вероятностью события 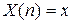 при единственном условии
при единственном условии 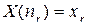 . Числа
. Числа 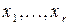 произвольны, а рассматриваемые события имеют положительные вероятности.
произвольны, а рассматриваемые события имеют положительные вероятности.
Таким образом, в определении 1 постулируется, что для заданного настоящего состояния системы 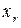 никакие дополнительные сведения относительно состояний системы в прошлом не могут изменить (условную) вероятность состояния x в некоторый будущий момент времени.
никакие дополнительные сведения относительно состояний системы в прошлом не могут изменить (условную) вероятность состояния x в некоторый будущий момент времени.
Дискретный марковский процесс также называется цепью Маркова, но описанный перед О1 процесс обладает дополнительным свойством: переходные вероятности 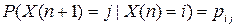 не зависят от n.
не зависят от n.
Обобщением описанной ситуации является случай, когда переходные вероятности 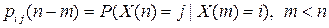 зависят только от разности
зависят только от разности 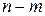 . Такая цепь Маркова называется однородной. В общей цепи Маркова переходные вероятности зависят от моментов времени и обозначаются
. Такая цепь Маркова называется однородной. В общей цепи Маркова переходные вероятности зависят от моментов времени и обозначаются 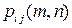 , так что
, так что 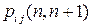 определяют вероятности перехода за один шаг. В дальнейшем рассматриваются только однородные цепи Маркова, для которых
определяют вероятности перехода за один шаг. В дальнейшем рассматриваются только однородные цепи Маркова, для которых 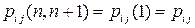
Теория цепей Маркова является простейшим обобщением схемы независимых испытаний Бернулли, в которой с каждым исходом 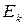 связывалась фиксированная вероятность
связывалась фиксированная вероятность 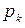 . В цепи Маркова каждой паре исходов
. В цепи Маркова каждой паре исходов  отвечает условная вероятность
отвечает условная вероятность 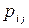 и должны быть заданы вероятности
и должны быть заданы вероятности 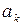 исходов
исходов 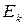 в начальном состоянии. Вероятности последовательных исходов в цепи Маркова удовлетворяют соотношению
в начальном состоянии. Вероятности последовательных исходов в цепи Маркова удовлетворяют соотношению
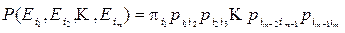 ,
,
причем начальному исходу удобно присваивать номер 1, второму – 2 и т. д.
Пусть цепь Маркова описывается начальным вектором вероятностей  ,
, 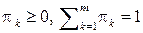 исходов (состояний)
исходов (состояний) 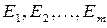 и квадратной матрицей вероятностей перехода
и квадратной матрицей вероятностей перехода
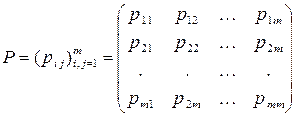 ,
,
причем 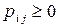 и
и 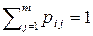 . Такая матрица называется стохастической.
. Такая матрица называется стохастической.
Любая стохастическая матрица может служить матрицей вероятностей перехода и вместе с начальным вектором вероятностей задает цепь Маркова.
Примеры цепей Маркова.
Графически цепь Маркова описывается направленным графом, вершины которого соответствуют состояниям цепи, а дуга, выходящая из состояния 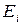 и направленная в состояние
и направленная в состояние 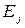 ,помечается вероятностью перехода
,помечается вероятностью перехода 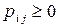 .
.
Аналогично предыдущему можно определить цепь Маркова с бесконечным числом состояний.
Из определения 1 следует, что вероятности перехода за n шагов можно найти по простой формуле
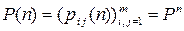 ,
,
т. е. с формальной точки зрения исследование многих свойств цепей Маркова сводится к изучению степеней матриц вероятностей перехода.
Для любых неотрицательных n и r справедливо уравнение Колмогорова-Чепмена 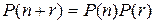 , где
, где 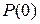 – единичная матрица.
– единичная матрица.
Пусть  – распределение вероятностей цепи Маркова на n -м шаге, причем
– распределение вероятностей цепи Маркова на n -м шаге, причем 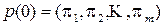 . Тогда имеем
. Тогда имеем
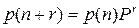 ,
, 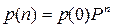 .
.
Пример цепи Маркова.
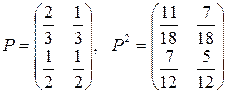 .
.
 2020-05-12
2020-05-12 211
211







