Определение 2. Говорят, что состояние 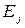 достижимо из состояния
достижимо из состояния 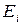 , если существует такое
, если существует такое  , что
, что 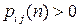 . Состояния
. Состояния 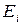 и
и 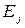 называются сообщающимися, если они достижимы друг из друга.
называются сообщающимися, если они достижимы друг из друга.
Множество состояний C цепи Маркова называется замкнутым, если никакое состояние вне C недостижимо из C. Цепь Маркова называется неразложимой, если каждое ее состояние достижимо из любого другого состояния, т. е. имеется всего одно замкнутое множество состояний.
Определение 3. Состояние 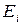 имеет период
имеет период  , если
, если 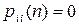 , пока n не является кратным d, и
, пока n не является кратным d, и  – наименьшее целое число, обладающее этим свойством. Состояние
– наименьшее целое число, обладающее этим свойством. Состояние 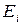 называется непериодическим, если такого
называется непериодическим, если такого  не существует.
не существует.
Пример. Простейшим примером цепи Маркова с периодом 3 является цепь с тремя состояниями, которая описывается матрицей переходов
 ,
,  ,
, 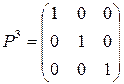 .
.
Изобразить орграф.
В неразложимой цепи Маркова все ее состояния имеют одинаковый период, в частности, все состояния являются непериодическими.
Вероятность возврата в состояние i равна  , где
, где  – вероятность возврата в состояние i ровно за n шагов, а среднее время возвращения в состояние i равно
– вероятность возврата в состояние i ровно за n шагов, а среднее время возвращения в состояние i равно  .
.
Определение 4. Состояние i называется возвратным, если вероятность возвращения в него равна  и невозвратным, если
и невозвратным, если  . Если для возвратного состояния
. Если для возвратного состояния  , то состояние i называется возвратным положительным, а при
, то состояние i называется возвратным положительным, а при  – возвратным нулевым.
– возвратным нулевым.
Пример. Для цепи Маркова с матрицей переходов за один шаг (изобразить орграф)
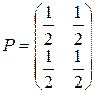
имеем  , а
, а  .
.
Возвратное состояние, не являющееся ни нулевым, ни периодическим, называется эргодическим.
Определение 5. Цепь Маркова называется эргодической, если для любых значений  существует
существует
 ,
,  .
.
Распределение вероятностей в О4 называется предельным (финальным) распределением.
Теорема 1. Если в конечной цепи Маркова в некоторый момент времени n все элементы матрицы 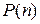 положительны, то цепь Маркова эргодическая.
положительны, то цепь Маркова эргодическая.
Определение 6. Распределение вероятностей  ,
, 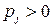 ,
,  называется стационарным распределением цепи Маркова, если для всех j выполняется следующее условие
называется стационарным распределением цепи Маркова, если для всех j выполняется следующее условие
 .
.
В частности, предельное распределение в определение 5 является стационарным.
Задачи
1. Цепь Маркова имеет матрицу вероятностей перехода
 .
.
Найти замкнутые множества состояний и определить возвратные и невозвратные состояния. Найти периоды периодических состояний.
2. Цепь Маркова задана начальным вектором вероятностей  и матрицей вероятностей перехода
и матрицей вероятностей перехода
 .
.
Найти:
а) распределение по состояниям в момент времени  ;
;
б) вероятность того, что в моменты  состояниями цепи будут соответственно
состояниями цепи будут соответственно 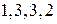 ;
;
в) стационарное распределение.
3. Найти предельное распределение для цепи Маркова с заданной матрицей вероятностей перехода за один шаг:
а)  ;
;
б) 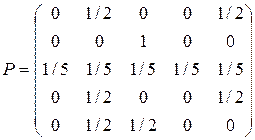 .
.
 2020-05-12
2020-05-12 258
258







