а. Пересчёт вектора правых частей системы (выполняется произведением матрицы коэффициентов на вектор найденных корней)
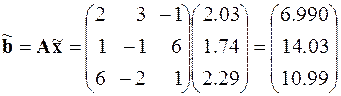
б. Формирование системы уравнений, определяющей погрешности решения
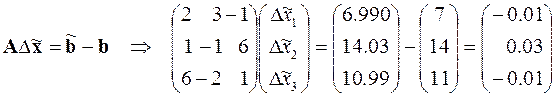 ,
,
то есть
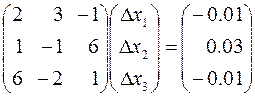
в. Решение системы относительно погрешностей оно выполняется аналогично пунктам 1 и 2. Прямой ход (пункт 1) даёт следующую систему с верхней треугольной матрицей
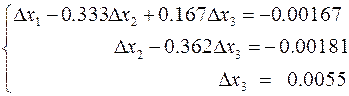 ,
,
а обратный ход позволяет получить решение
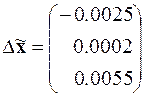 .
.
г. Оценка абсолютной и относительной погрешностей решения системы линейных алгебраических уравнений
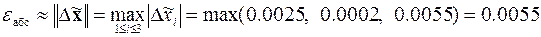 ,
,
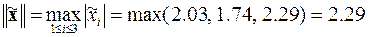 ,
,
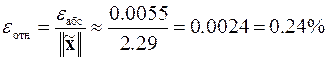 .
.
О выборе метода решения систем уравнений
Каждый из рассмотренных методов имеет свои достоинства и недостатки. В частности, метод Гаусса позволяет получить решение за конечное число шагов. Для этого требуется выполнить n (n 2 + 3 n – 1)/3 операций умножения и деления и n (n – 1)(2 n + 5)/6 операций сложения и вычитания, количество которых при больших порядках системы (n > 100) можно принять равным n 3/3 в обоих случаях. Однако его методические ошибки, связанные с размером разрядной сетки вычислений, резко нарастают с увеличением порядка системы и не позволяют применять его для систем высоких порядков без использования специальных приёмов.
Итерационные методы позволяют получать решение систем бóльшего порядка. Для выполнения каждой итерации с их помощью необходимо выполнить n (n + 1) операций умножения и деления и столько же операций сложения и вычитания. При больших порядках системы уравнений (n > 100) их количество можно принять равным n 2. Из сравнения трудоёмкости итерационных методов и метода Гаусса следует оценка, которой можно руководствоваться при окончательном выборе метода решения системы при необходимости его многократного нахождения. Если количество итераций, требуемое для получения решения системы итерационными методами, не превышает n /3, то выгоднее применять их, а не методы типа Гаусса. Однако здесь следует помнить, что итерационные методы требуют, чтобы матрица системы обладала определёнными свойствами, обеспечивающими их сходимость. Необходимо также отметить, что выполнение этих требований часто не гарантирует высокой скорости их сходимости.
2. Задание: запрограммируйте метод Гаусса с выбором главного элемента для решения системы уравнений.
 2020-05-12
2020-05-12 91
91







