2020-05-12
359
Дисциплина: «Основы высшей математики»
Специальность: « Переводческое дело» ОП 9-Б
Подготовила Курманова А.Б.
Лекция 02.04.20 г.
Раздел 4: Дифференциальное исчисление
Тема: Понятие производной и ее геометрический и физический смысл
На уроке мы вспомним, что такое производная функции, разберемся, как вычислять производные некоторых функций, вспомним геометрический и физический смысл производной. Рассмотрим примеры вычисления основных производных. Типовые задачи
Понятие производной
Пусть задана некоторая функция y=f(x). Возьмем какое-нибудь значение x 0из области определения этой функции: x0∈D[f]. Соответствующее значение функции в этой точке будет равно y0=f(x0).
Приращение аргумента и функции
Определение
Приращением аргумента называется разность между двумя значениями аргумента: "новым" и "старым".
Обычно обозначается как Δx=x1−x0.
Пример
Задание. Найти приращение аргумента x если он переходит от значения 3 к значению 3,2.
Решение. Искомое приращение: Δx=3,2−3=0,2.
|
|
|
Ответ. Δx=0,2
Зададим аргументу x 0 приращение Δ x. А тогда значение функции в новой точке f(x0+Δx).
Определение
Приращением функции y=f(x) в точке x 0, соответствующее приращению аргумента Δx=x−x0, называется величина:
Δy=f(x0+Δx)−f(x0)
Пример
Задание. Найти приращение функции y=2x2 при x0=3 и Δx=0,1
Решение. Подставляя в формулу, получаем, что приращение функции:
Δy=y(3+0,1)−y(3)=2⋅(3+0,1)2−2⋅32=1,22
Ответ. Δy=1,22
Определение производной
Определение
Производной y′(x) от функции y=f(x) в точке x 0 называется предел отношения приращения функции Δ y к приращению аргумента Δ x: Δ y Δ x при Δx→0, если он существует, то есть:
y′(x0)=f′(x0)=limΔx→0ΔyΔx=limΔx→0f(x0+Δx)−f(x0)Δx
или
y′(x0)=limx→x0f(x)−f(x0)x−x0
Пример
Задание. Найти производную функции y=x2+3x в точке x 0=0.
Решение. Найдем приращение заданной функции в точке x 0:
Δ y = y (0+Δ x)− y (0)= y (Δ x)− y (0)=Δy=y(0+Δx)−y(0)=y(Δx)−y(0)=
=(Δ x)2+3Δ x −0=Δ x (Δ x +3)=(Δx)2+3Δx−0=Δx(Δx+3)
Тогда
y′(0)=limΔx→0Δx(Δx+3)Δx=limΔx→0(Δx+3)=0+3=3
Ответ. y′(0)=3
Начнем с самого простого – с линейной функции.
Пусть 
, где 
и 
– некоторые числа, а 
– переменная.
Тогда:
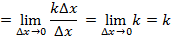
Итак, выясняется, что 
для любого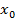 
. Значит, можно утверждать, что 
.
О чем это говорит?
Во-первых, мы подтвердили несколько фактов про линейную функцию, которые нам, возможно, уже были известны.
1. Так, исходя из геометрического смысла производной, тангенс угла наклона прямой совпадает с ее угловым коэффициентом (он равен производной в соответствующей точке).
|
|
|
Кроме этого, мы видим, что раз производная постоянна, то угол наклона постоянен, это вполне соответствует нашим представлениям о прямой.
2. Если предположить, что материальная точка движется прямолинейно равномерно, то ее координата в данный момент времени описывается функцией: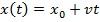 
, где 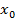– начальная координата, а 
– скорость. Рассмотрим это утверждение.
Предположим, что есть некоторая материальная точка, которая двигается по закону 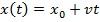. Найти его производную.
Решение
Для удобства предположим, что точка движется равномерно, то есть в каждой точке одинаково. Тогда с точки зрения физического смысла мы получим:
.
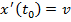Производная функции 
в точке :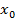 
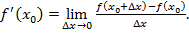
Геометрический смысл производной
Если задан график функции , то производная в точке 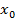– это тангенс угла наклона касательной к данной функции в точке c абсциссой 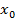(или угловой коэффициент касательной).
Физический смысл производной
Если в качестве функции мы берем перемещение, зависящее от 
, – 
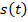, то 
, где 
– перемещение, – время, а – мгновенная скорость в данной точке.
И сегодня мы попробуем вычислить некоторые производные по определению.
Физический смысл производной: производная от координаты равна мгновенной скорости точки в данный момент времени.
Но для равномерного движения мгновенная скорость в любой момент времени одна и та же и равна скорости движения тела . Получаем, что должно выполняться равенство: 
.
