Примеры реализации: «Задача распределения ресурса»

Метод ветвей и границ

Идея метода ветвей и границ достаточно простая:

 - Разбить исходную задачу (большой размерности и сложности получения оптимального решения) на ряд задач (подзадач) меньшей размерности – процесс ветвления;

- Искать решения в полученных подзадачах с направленным их перебором в направлении снижения их значимости для достижения окончательного оптимального решения;

- В процессе решения исключать из рассмотрения (элиминировать) подзадачи в которых не могут быть оптимальных решений. Для каждой подзадачи нужно построить функцию оценки предельного значения целевой функции (границы), которая используется для исключения подзадач из рассмотрения. Этот процесс исключает полный перебор множества допустимых решений. 

Таким образом, для реализации метода ветвей и границ нужно определить для каждой задачи (постановки) процедуры (правила):

- Разбиения задачи на подзадачи;

- Построения оценки целевой функции для каждого подзадачи (снизу для задач на минимум, и сверху для задач на максимум целевой функции);

- Правило выбора очередной подзадачи для рассмотрения;

- Правило исключения подзадачи из рассмотрения (элиминации).

При простоте общей схемы метода решения, конкретная реализация для задачи является определенным искусством!

Примеры реализации: «Задача распределения ресурса»

Описательная постановка задачи:

Пусть имеется ресурс объемом A, который может быть распределен между n проектами. Каждый проект обеспечивает эффект (доходность, прибыль) от полученного ресурса в объеме c_i, i=1,2,…,n при получении ресурса объемом a_i.

Требуется распределить ресурсы между проектами с целью получения максимального эффекта.

Формализованные постановки задачи:

Вариант 1. Пусть проекты могут быть обеспечены ресурсом в полном объеме, и эффект получаем в соответствии с долей обеспечения ресурсами этого проекта.

Обозначим:

х_i – объем обеспечения потребности в ресурсах проекта i, 0≤x_i≤1;

Тогда суммарный эффект- целевая функция имеет вид:

,

при ограничениях

,

.

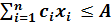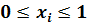Это задача линейного программирования, с непрерывными переменными имеет достаточно тривиальное решение.

Поскольку задача на нахождение максимума, в первую очередь средства должны быть распределены на проекты с наибольшей «отдачей» эффектом, выражаемая коэффициентом .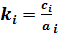

Упорядочим проекты в порядке убывания коэффициентов . Пусть проекты упорядочены в порядке убывания , т.е. 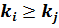, для всех .

Тогда оптимальное решение имеет вид:

Разберем пример.

Пусть А =100, n =4, a_i и с_i приведены в таблице

i	1	2	3	4
ai	40	25	30	20
сi	40	75	36	40

 

Вычислим коэффициенты .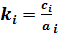

i	1	2	3	4
ai	40	30	45	40
сi	40	90	54	80
	1	3	1,2	2

 

Упорядочим проекты в порядке убывания коэффициентов .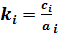

i (старый)	2	4	3	1
i (новый)	1	2	3	4
ai	30	40	45	40
сi	90	80	54	40
	3	2	1,2	1

 

В соответствии с вышеприведенным определением оптимального решения получаем

i (новый)	1	2	3	4
ai	30	40	45	40
сi	90	80	54	40
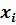
	1	1	0,667	0
	30	70	115	155

 

Оптимальное значение целевой функции

 

Вариант 2. Пусть проекты могут быть реализовываться только в полном объеме, либо вовсе не реализуется.

Это принципиально меняет постановку задачи.

Обозначим:

х_i =1, если проект реализуется, х_i =0, если проект не реализуется.

Тогда суммарный эффект- целевая функция имеет вид:

,

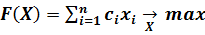при ограничениях

,

.

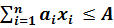Это задача линейного целочисленного программирования, с дискретными (двоичными, булевыми) переменными.

Решением задачи будет допустимый вектор

.

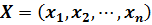Множество допустимых решений включает 2ⁿ решений

Рассмотрим метод ветвей и границ для решения данной задачи.

Определим коэффициенты «отдачи» проекта, определяемые .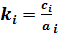

Упорядочим проекты в порядке убывания коэффициентов .

Пусть проекты упорядочены в порядке убывания , т.е. 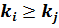, для всех .

Разбиения задачи на подзадачи: производим на множестве допустимых решений следующим образом.

Множество допустимых решений разбивается на два непересекающиеся подмножества по некоторой переменной x_i.

В первую включаем решения с x_i=1, а во вторую с x_i=0.