Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители. (Если вы не помните, что такое нули функции и знак функции на промежутке – смотрите статью «Исследование графика функции»).
Напомним, как раскладывается на множители квадратный трехчлен, то есть выражение вида 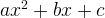 .
.
 , где
, где 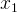 и
и  — корни квадратного уравнения
— корни квадратного уравнения  .
.
Получим:
Рисуем ось 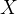 и расставляем точки, в которых числитель и знаменатель обращаются в нуль.
и расставляем точки, в которых числитель и знаменатель обращаются в нуль.

Нули знаменателя  и
и  - выколотые точки, так как в этих точках функция в левой части неравенства не определена (на нуль делить нельзя). Нули числителя
- выколотые точки, так как в этих точках функция в левой части неравенства не определена (на нуль делить нельзя). Нули числителя  и
и  - закрашены, так как неравенство нестрогое. При
- закрашены, так как неравенство нестрогое. При  и
и  наше неравенство выполняется, так как обе его части равны нулю.
наше неравенство выполняется, так как обе его части равны нулю.
Эти точки разбивают ось 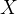 на
на  промежутков.
промежутков.
Определим знак дробно-рациональной функции в левой части нашего неравенства на каждом из этих промежутков. Мы помним, что дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Это значит, что на каждом из промежутков между точками, где числитель или знаменатель обращаются в нуль, знак выражения в левой части неравенства будет постоянным - либо "плюс", либо "минус".
И поэтому для определения знака функции на каждом таком промежутке мы берем любую точку, принадлежащую этому промежутку. Ту, которая нам удобна.

 . Возьмем, например,
. Возьмем, например,  и проверим знак выражения в левой части неравенства. Каждая из "скобок" отрицательная. Левая часть имеет знак
и проверим знак выражения в левой части неравенства. Каждая из "скобок" отрицательная. Левая часть имеет знак  .
.
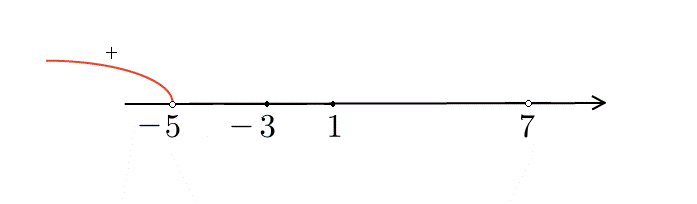
 Следующий промежуток:
Следующий промежуток:  . Проверим знак при
. Проверим знак при  . Получаем, что левая часть поменяла знак на
. Получаем, что левая часть поменяла знак на  .
.

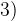
 . Возьмем
. Возьмем 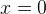 . При
. При 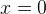 выражение положительно - следовательно, оно положительно на всем промежутке от
выражение положительно - следовательно, оно положительно на всем промежутке от  до
до  .
.

 При
При 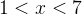 левая часть неравенства отрицательна.
левая часть неравенства отрицательна.

 И, наконец,
И, наконец,  . Подставим
. Подставим  и проверим знак выражения в левой части неравенства. Каждая "скобочка" положительна. Следовательно, левая часть имеет знак
и проверим знак выражения в левой части неравенства. Каждая "скобочка" положительна. Следовательно, левая часть имеет знак  .
.
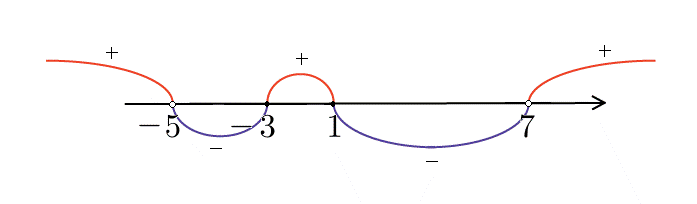
Мы нашли, на каких промежутках выражение положительно. Осталось записать ответ:
Ответ:  .
.
Обратите внимание: знаки на промежутках чередуются. Это произошло потому, что при переходе через каждую точку ровно один из линейных множителей поменял знак, а остальные сохранили его неизменным.
Мы видим, что метод интервалов очень прост. Чтобы решить дробно-рациональное неравенство методом интервалов, приводим его к виду:
 , или
, или  , или
, или  , или
, или  .
.
(в левой части - дробно-рациональная функция, в правой - нуль).
Затем - отмечаем на числовой прямой точки, в которых числитель или знаменатель обращаются в нуль.
Эти точки разбивают всю числовую прямую на промежутки, на каждом из которых дробно-рациональная функция сохраняет свой знак.
Остается только выяснить ее знак на каждом промежутке.
Мы делаем это, проверяя знак выражения  в любой точке, принадлежащей данному промежутку. После этого - записываем ответ. Вот и всё.
в любой точке, принадлежащей данному промежутку. После этого - записываем ответ. Вот и всё.
Но возникает вопрос: всегда ли знаки чередуются? Нет, не всегда! Надо быть внимательным и не расставлять знаки механически и бездумно.
2. Рассмотрим еще одно неравенство.

Снова расставляем точки на оси 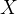 . Точки
. Точки  и
и  - выколотые, поскольку это нули знаменателя. Точка
- выколотые, поскольку это нули знаменателя. Точка  - тоже выколота, поскольку неравенство строгое.
- тоже выколота, поскольку неравенство строгое.

При 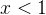 числитель положителен, оба множителя в знаменателе отрицательны. Это легко проверить, взяв любое число с данного промежутка, например,
числитель положителен, оба множителя в знаменателе отрицательны. Это легко проверить, взяв любое число с данного промежутка, например, 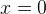 . Левая часть имеет знак
. Левая часть имеет знак  :
:

При  числитель положителен; первый множитель в знаменателе положителен, второй множитель отрицателен. Левая часть имеет знак
числитель положителен; первый множитель в знаменателе положителен, второй множитель отрицателен. Левая часть имеет знак  :
:

При  ситуация та же! Числитель положителен, первый множитель в знаменателе положителен, второй отрицателен. Левая часть имеет знак
ситуация та же! Числитель положителен, первый множитель в знаменателе положителен, второй отрицателен. Левая часть имеет знак  :
:

Наконец, при 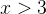 все множители положительны, и левая часть имеет знак
все множители положительны, и левая часть имеет знак  :
:

Ответ: 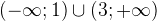 .
.
Почему нарушилось чередование знаков? Потому что при переходе через точку  "ответственный" за неё множитель
"ответственный" за неё множитель  не изменил знак. Следовательно, не изменила знак и вся левая часть нашего неравенства.
не изменил знак. Следовательно, не изменила знак и вся левая часть нашего неравенства.
Вывод: если линейный множитель  стоит в чётной степени (например, в квадрате), то при переходе через точку
стоит в чётной степени (например, в квадрате), то при переходе через точку  знак выражения в левой части не меняется. В случае нечётной степени знак, разумеется, меняется.
знак выражения в левой части не меняется. В случае нечётной степени знак, разумеется, меняется.
3. Рассмотрим более сложный случай. От предыдущего отличается тем, что неравенство нестрогое:
Левая часть та же, что и в предыдущей задаче. Та же будет и картина знаков:

Может, и ответ будет тем же? Нет! Добавляется решение  Это происходит потому, что при
Это происходит потому, что при  и левая, и правая части неравенства равны нулю - следовательно, эта точка является решением.
и левая, и правая части неравенства равны нулю - следовательно, эта точка является решением.
Ответ:  .
.
В задаче  на ЕГЭ по математике такая ситуация встречается часто. Здесь абитуриенты попадают в ловушку и теряют баллы. Будьте внимательны!
на ЕГЭ по математике такая ситуация встречается часто. Здесь абитуриенты попадают в ловушку и теряют баллы. Будьте внимательны!
4. Что делать, если числитель или знаменатель не удается разложить на линейные множители? Рассмотрим такое неравенство:

Квадратный трехчлен  на множители разложить нельзя: дискриминант отрицателен, корней нет. Но ведь это и хорошо! Это значит, что знак выражения
на множители разложить нельзя: дискриминант отрицателен, корней нет. Но ведь это и хорошо! Это значит, что знак выражения  при всех
при всех  одинаков, а конкретно - положителен. Подробнее об этом можно прочитать в статье о свойствах квадратичной функции.
одинаков, а конкретно - положителен. Подробнее об этом можно прочитать в статье о свойствах квадратичной функции.
И теперь мы можем поделить обе части нашего неравенства на величину  , положительную при всех
, положительную при всех  . Придём к равносильному неравенству:
. Придём к равносильному неравенству:

- которое легко решается методом интервалов.
Обратите внимание - мы поделили обе части неравенства на величину, о которой точно знали, что она положительна. Конечно, в общем случае не стоит умножать или делить неравенство на переменную величину, знак которой неизвестен.
5. Рассмотрим еще одно неравенство, на вид совсем простое:

Так и хочется умножить его на  . Но мы уже умные, и не будем этого делать. Ведь
. Но мы уже умные, и не будем этого делать. Ведь  может быть как положительным, так и отрицательным. А мы знаем, что если обе части неравенства умножить на отрицательную величину - знак неравенства меняется.
может быть как положительным, так и отрицательным. А мы знаем, что если обе части неравенства умножить на отрицательную величину - знак неравенства меняется.
Мы поступим по другому — соберём всё в одной части и приведём к общему знаменателю. В правой части останется нуль:


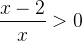
И после этого - применим метод интервалов
 2020-05-12
2020-05-12 708
708







