2020-05-12
492
Кодирование целых чисел, имеющих знак, можно осуществить двумя способами.
Первый способ – называется прямым кодом. При этом один (старший) разряд в машинном слове (напомним, здесь машинное слово – 16 разрядов) отводится для записи знака числа; при этом условились кодировать знак «+» нулем, а знак «-» единицей. Под запись самого числа, очевидно, остается 15 двоичных разрядов, что обеспечивает наибольшее значение числа 
. Однако прямое кодирование усложняет вычисления. Например, операция сложения двух чисел с разными знаками должна быть заменена операцией вычитания меньшего из большего с последующим присвоением результату знака большего по модулю числа. Таким образом, такая операция сопровождается рядом проверок условий и выработкой признаков, в соответствии с которыми выбирается то или иное действие.
Второй способ - кодирования целых чисел со знаком называется дополнительным кодированием. Идея построения дополнительного кода такова: на оси целых чисел (
– всего 65536 чисел), помещающихся в машинное слово (в 16 разрядов) сместим положение нуля к середине интервала. При этом числа из первой половины (
) интервала будем считать положительными, а числа из второй половины (
) будем считать отрицательными. Судить о знаке числа можно по его величине, и в явном виде выделение знака не требуется. 
Оказывается, что принадлежность кода к интервалу кодов положительных или отрицательных чисел также видна по состоянию старшего бита – у кодов положительных чисел его значение «0», а у кодов отрицательных – «1». Это напоминает представление чисел с помощью прямого кода, но принцип построения дополнительного кода другой. Применение дополнительного кода позволяет заменить вычитание чисел их суммированием в дополнительном коде.
Рассмотрим вычитание числа 
, что эквивалентно прибавлению 
.
При наличии k разрядов можно закодировать 
чисел в P -ичной системе счисления. При этом максимальное k -разрядное P -ичное число есть 
, а число (оно содержит 
разрядов) можно считать нулем, так как первые слева (младшие) k разрядов (битов) в числе 
нулевые, а старший, единичный бит в нем уже не входит в отведенную разрядную сетку. Таким образом, можно записать:
. (12.5)
Однако вычесть 
из будет удобнее, если (12.5) преобразовать:
, (12.6)
причем число 
есть максимальное P -ичное k -разрядное число 
, каждая его цифра равна 
:
, (12.7)
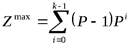, (12.8)
Цифры числа Zобозначим 
:
. (12.9)
Таким образом, с учетом (12.8) и (12.9), выражение (12.7) легко преобразуется:
. (12.10)
Величина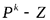 
(12.10) называется дополнением 
целого k-разрядного числа Z в системе счисления P.
Пример.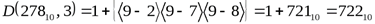 
;
.
Важным свойством дополнения является то, что его сумма с исходным числом в заданной разрядной сетке равна нулю, то есть
. (12.11)
Пример. 
;
.
В этом примере единица в скобках должна быть отброшена, так как она выходит за отведенную разрядную сетку.
Из (12.11) логично заключить, что
, (12.12)
значит, при 
имеем
. (12.13)
Поэтому дополнительный код (DС) двоичных чисел в компьютере надо строить согласно следующему правилу:
- для
дополнительный код совпадает с самим числом, то есть 
; - для дополнительный код совпадает с дополнением модуля числа, то есть
.
Пример. Построить дополнительный двоичный код числа 
.
;
Пример. Построить дополнительный двоичный код числа 
.
.
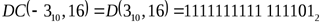Кстати, используя результаты этих примеров, легко убедиться, что
.
Прямые и дополнительные коды целых чисел со знаком сопоставлены в табл. 19.
В компьютере используется интервал 
целых чисел со знаком, закодированных дополнительным двоичным кодом. Именно таким является диапазон значений чисел типа Integer в языке PASCAL.
В компьютере перевод в дополнительный код осуществляется автоматически при вводе чисел. Именно в таком виде числа хранятся в ОЗУ и участвуют в арифметических операциях.
Если результат отрицательный, то прямой код модуля числа получают из дополнительного кода в обратном изложенному порядке: 
-я цифра числа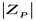 
равна разности значения P и 
-й цифры числа 
.
