Достаточные условия оптимальности

1 2

Постановка задачи.

Пусть поведение объекта управления описывается системой обыкновенных дифференциальных уравнений (ОДУ)

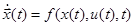(1)

где: 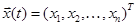- вектор состояния системы, ;

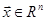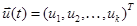- вектор управления, 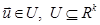, U – заданное множество допустимых управлений;

t – время, 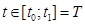- интервал времени функционирования системы;

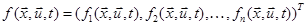- непрерывная вместе со своими частными производными вектор-функция, 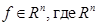- n -мерное евклидово пространство,

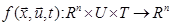Момент начала процесса t ₀ задан, а момент окончания процесса t ₁ или задан, или определяется первым моментом достижения точкой 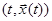некоторой заданной гиперповерхности ,

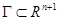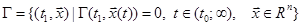, (2)

т.е. в момент времени t ₁ должно выполняться условие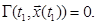

b). Функционал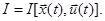

Требуется определить вектор функции 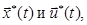доставляющие минимум заданному функционалу при переводе системы из начального состояния 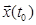в конечное состояние .

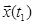Начальное условие 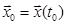заранее не задано и может быть произвольно на множестве .

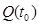Произвольность начального значения 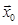понимается в следующем смысле:

Пусть 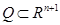- множество точек 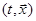, из которых можно достигнуть терминального множества Г по некоторой траектории, соответствующей допустимому управлению. Тогда 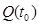- сечение множества Q при фиксированном t = t₀.

Задано множество допустимых управлений U₀, элементами которого являются кусочно-непрерывные функции u(t) со значениями в множестве .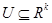

Задано множество допустимых процессов D, элементами которого являются тройки 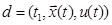, которые включают момент окончания процесса, траекторию x(t) и управление u(t), где для любого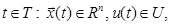 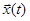непрерывные и кусочно-непрерывно дифференцируемые, u(t) – кусочно-непрерывные, удовлетворяющие уравнению (1) с начальным условием 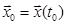и условию (2).

На множестве допустимых процессов D определен функционал качества управления

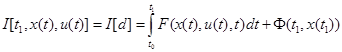(3)

где 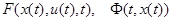- заданные непрерывно дифференцируемые функции.

Предполагается, что при управлении используется информация о времени t и всех координатах вектора состояния .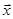

Множество допустимых управлений с полной обратной связью U_n образуют функции 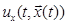которые для каждого начального состояния 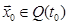порождают соответствующие тройки 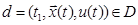, в которых программное управление 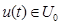, а для любого .

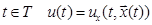Управление с полной обратной связью схематично представлено на рис. 1.

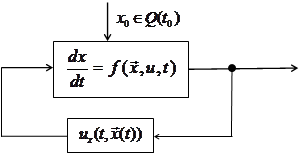Рис. 1.

Требуется найти такую функцию 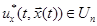, чтобы функционал (3) на этой функции достигал минимума

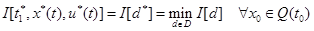(4)

где .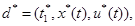

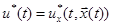Функция 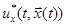называется оптимальным управлением с полной обратной связью, а формула, описывающая эту функцию, является уравнением оптимального регулятора в системе с полной обратной связью.

Для любого начального состояния 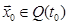функция 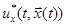порождает оптимальную траекторию 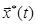, оптимальное управление 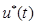и оптимальное время окончания процесса .

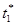Достаточные условия оптимальности.

Достаточные условия оптимальности управления с полной обратной связью определяются следующей теоремой.

Теорема. Если существует функция 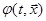, удовлетворяющая уравнению Беллмана

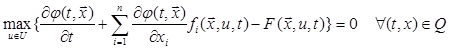(5)

с граничными условиями 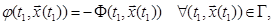и управление 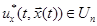, удовлетворяющее условию

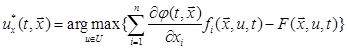, (6)

то 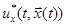является оптимальным управлением с полной обратной связью в задаче (4).

При этом минимальное значение функционала равно .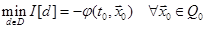

Примечание. Аргумент максимизации (argmax или arg max) — значение аргумента, при котором данное выражение достигает максимума. argmax x f (x) {\displaystyle {\underset {x}{\operatorname {argmax} }}\,f(x)} 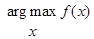есть значение х x {\displaystyle x}, при котором 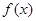f (x) {\displaystyle f(x)} достигает своего наибольшего значения. Является решением задачи 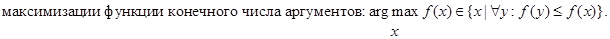argmax x f (x) ∈ { x | ∀ y: f (y) ≤ f (x) } {\displaystyle {\underset {x}{\operatorname {argmax} }}\,f(x)\quad \in \quad \{x\ |\ \forall y:f(y)\leq f(x)\}}

Аргумент максимизации определяется единственным образом тогда и только тогда, когда максимум достигается в единственной точке: 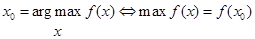x 0 = argmax x f (x) ⇔ max f (x) = f (x 0) {\displaystyle x_{0}={\underset {x}{\operatorname {argmax} }}\,f(x)\Leftrightarrow \max f(x)=f(x_{0})}