Вероятность произведения независимых событий

Два события называются независимыми, если вероятность одного из них не меняется при наступлении другого.

Такие события могут наступить при проведении двух независимых опытов. Если число исходов первого опыта 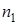, а число исходов второго , то общее число исходов при одновременном проведении двух опытов 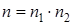. Если 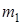исходов благоприятствуют событию 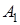, а 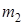— событию 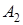, то общее число способов осуществить пару событий равно , тогда

Вероятность произведения независимых событий равна произведению вероятностей этих событий.

Вероятность произведения зависимых событий

Событие 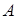называется зависимым от события 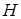, если вероятность события 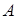меняется при наступлении события .

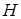Условной вероятностью 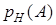события 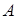относительно события 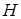называется вероятность события 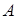, вычисленная в предположении, что событие 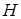наступило.

Пусть 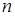общее число возможных исходов опыта, из них 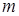исходов благоприятствуют событию Н. Предположим, что событие Н произошло. По определению:

Тогда 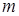— будет общим числом возможных исходов для события А. Пусть из них благоприятствуют событию А, а значит и событию АН. Тогда вероятность одновременного наступления событий и А и Н, т.е. их произведения, равна

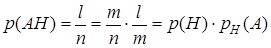Вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие наступило.

Эта формула носит название теоремы умножения вероятностей.

Пример. В корзине 10 шаров. Из них 5 белых. Наугад достают 2 шара. Найти вероятность того, что оба они белые.

Н – первый шар белый, Р(Н) = 5/10 = 1/2;

А — второй шар белый, Р (А) = 4/9;