2020-05-11
297
Найти пределы интегрирования.
Выяснить какой формулой площади плоской фигуры удобно пользоваться в данном случае.
Вычислить площадь заданной фигуры.
Задача 1. Найти площадь фигуры, ограниченной линией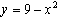 
Решение: решение задачи начинаем с анализа линии (или линий), входящих в условие задачи. 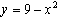— парабола, симметричная относительно оси ОУ с вершиной в т. С (0;9) (при х = 0, у = 9), ветвями направленными вниз (перед 
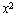стоит знак "–"). Для построения параболы необходимо знать три точки, одна из которых обязательно должна быть вершиной. Координаты вершины уже определены. Так как вершина находится выше оси ОХ и ее ветви направлены вниз, то две другие точки параболы можно найти как точки пересечения с осью ОХ. Для этого решаем уравнение: 
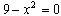, отсюда 9 = 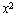х = 3. Следующий шаг — построение параболы. Чертим прямоугольную систему координат и по трем точкам приблизительно строим параболу.
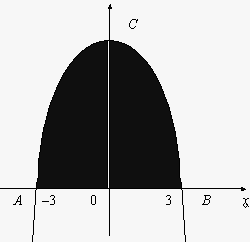
Заштриховываем фигуру, площадь которой надо найти. Следующий шаг — находим пределы интегрирования. Это вертикали, ограничивающие с боков площадь. В нашем примере: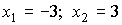 
. Согласно геометрическому смыслу производной:
|
|
|
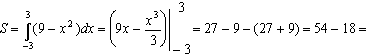36 КВ.ЕД
Если фигура симметрична относительно осей координат, то удобно вычислить половину площади и умножить полученное значение на 2.
Задача 2. Найти площадь фигуры, ограниченной линиями: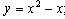 
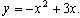
Решение: Анализируем линии, входящие в задание. Это кривые второго порядка — параболы. Для построения парабол находим их вершины и точки пересечения парабол с осью ОХ. Вершины парабол находятся по формулам:
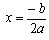, где а и b — параметры в квадратном уравнении 
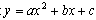. Ординаты находятся путем подстановки абсцисс в соответствующее уравнение параболы. Для первой параболы: 
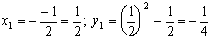Координаты вершин первой параболы 
.
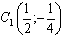Для второй параболы:
.
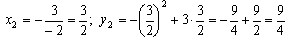Координаты вершины второй параболы: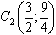 
.
Точка пересечения первой параболы с осью ОХ:
.
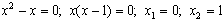Точка пересечения второй параболы с осью ОХ:
.
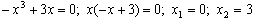Строим параболы.
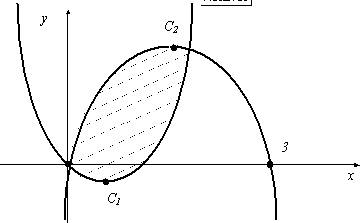
Площадь фигуры, находящуюся между параболами (заштрихованную), надо найти.
Найдем точки пересечения парабол. Это будут пределы интегрирования. Для этого решим систему уравнений:
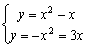Левые части (у) уравнений равны, значит равны и правые.
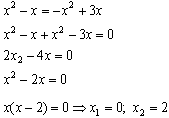— это вертикали, ограничивающие с боков площадь фигуры.
Для нахождения площади, заключенной между двумя линиями, существует правило: интеграл по верхней линии минус интеграл по нижней линии, пределы интегрирования — точки пересечения этих линий, т.е.:
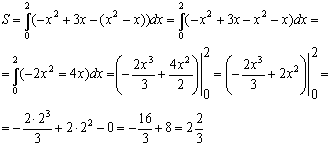
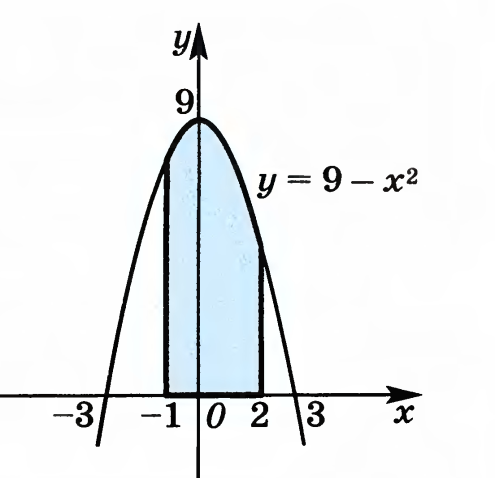
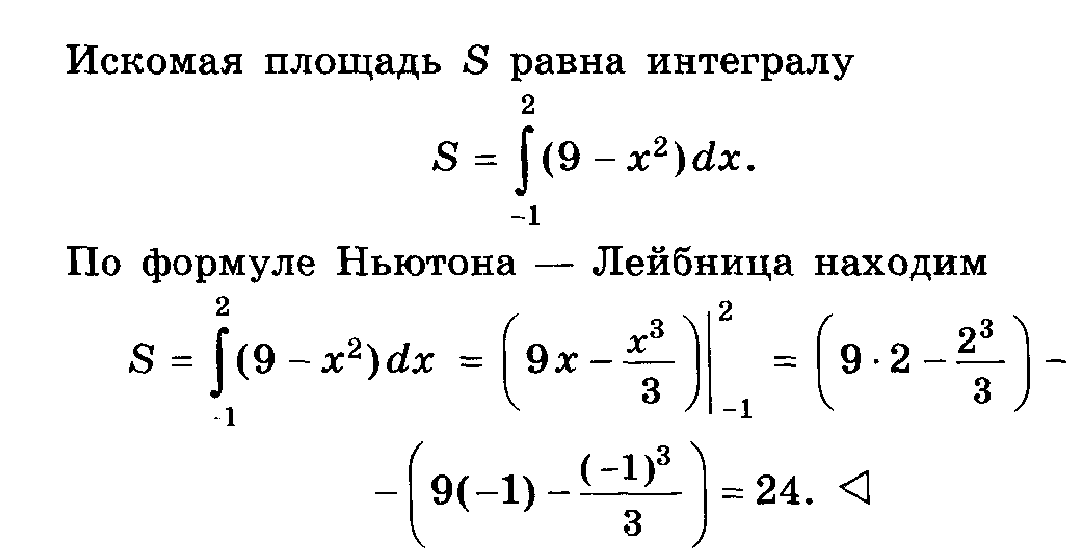
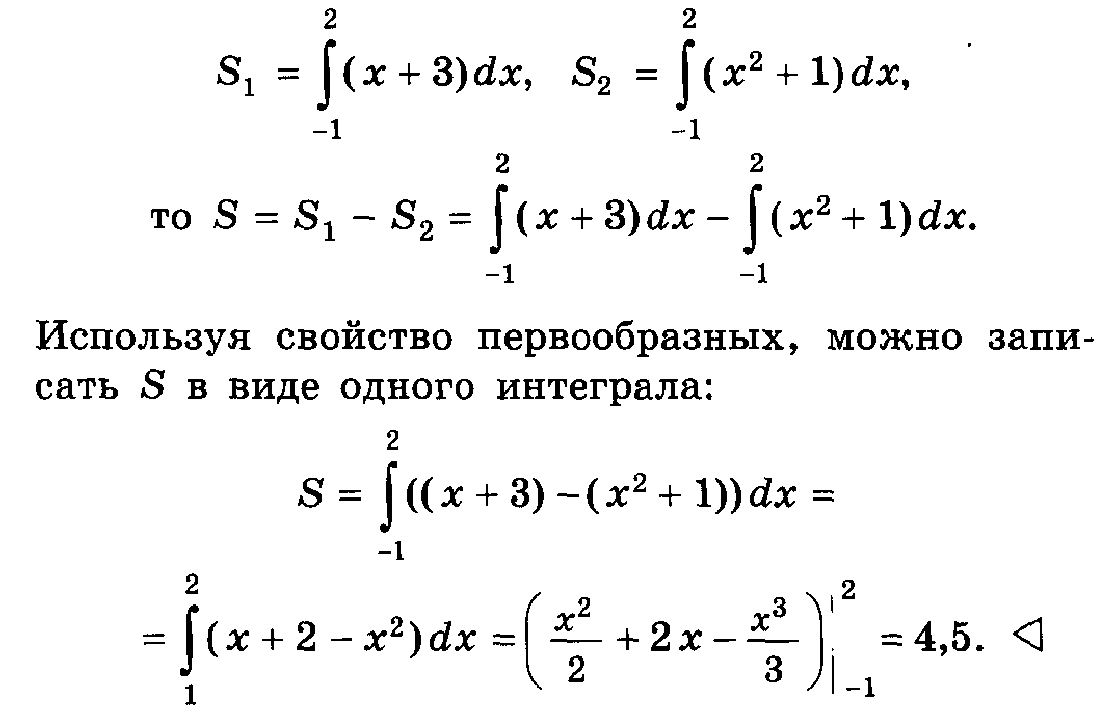
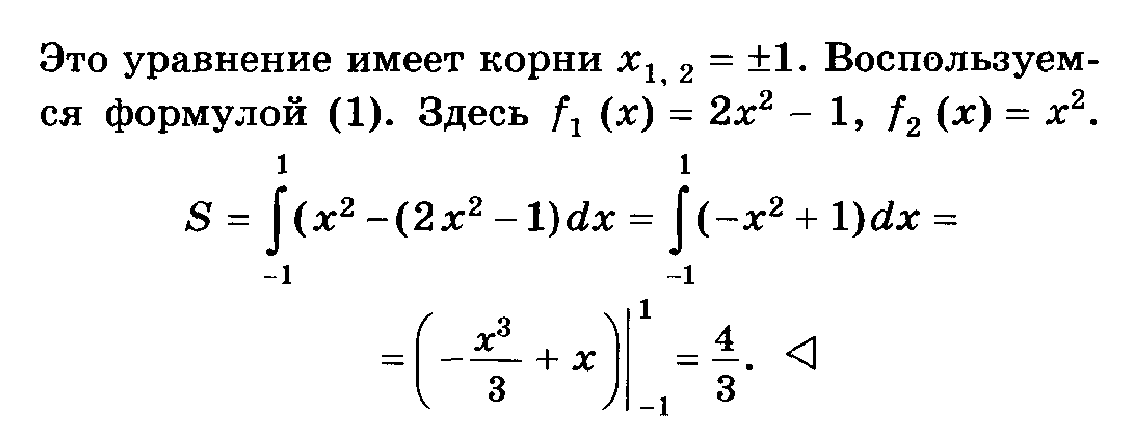
.Вычислить площадь криволинейной трапеции, ограниченной линиями у = 4 – х2 и у = 0
Решение:
1. Построим криволинейную трапецию:
|
|
|
у = 4 – х2- квадратичная функция, график – парабола, ветви направлены вниз.
у = 0 – ось абсцисс.
2. Найдём [а;b]:
4-х2 = 0; х2 = 4
х = -2 или х = 2, т. е. а = -2 b = 2
3. Найдём площадь криволинейной трапеции по формуле: S = F(b) – F(а)
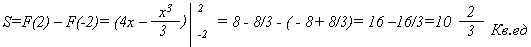
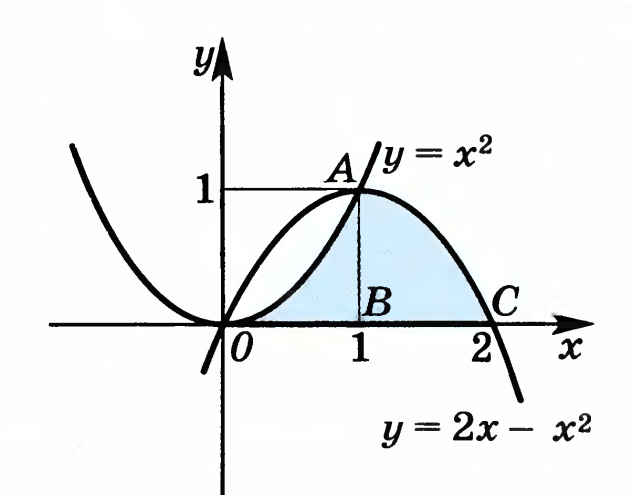
.Найти площадь фигуры, ограниченной линиями y = x, y = x2, x = 2.
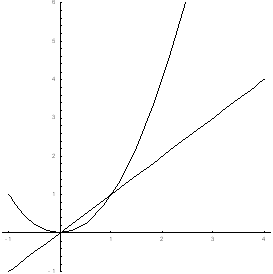Рисунок 3.
Искомая площадь (заштрихована на рисунке) может быть найдена по формуле:
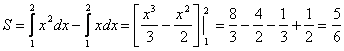(ед2)
Задания для самостоятельного выполнения
Тема: Вычисление площадей плоских фигур с помощью определенного интеграла.
Цели: - сформировать навык нахождения площадей плоских фигур с помощью определенного интеграла в ходе решения упражнений
Методические указания для выполнения заданий:
Таблица основных интегралов.
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
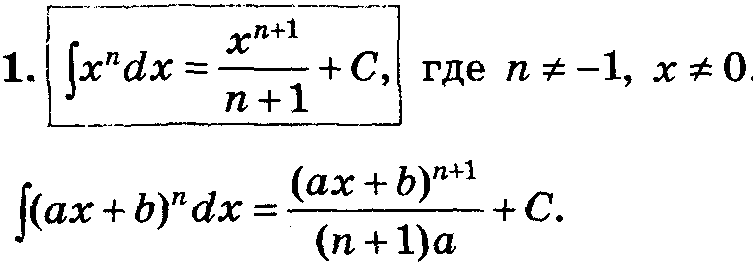
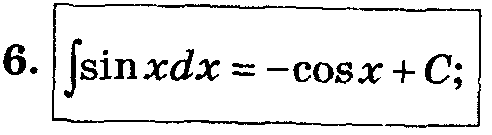
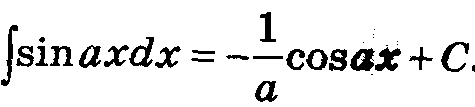
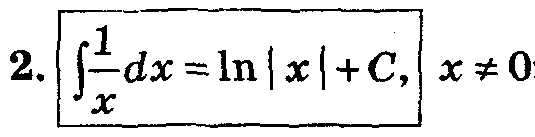
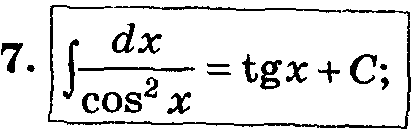
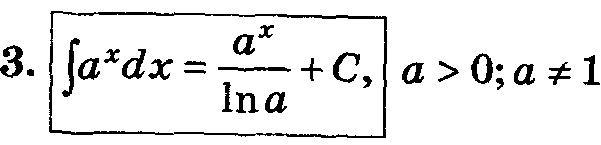
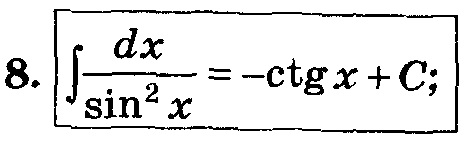
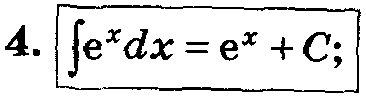
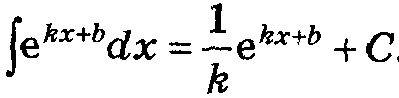
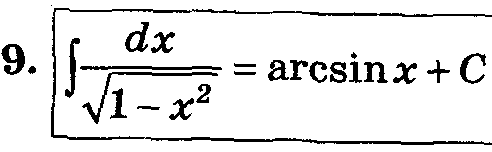
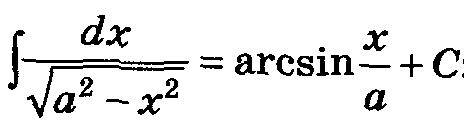
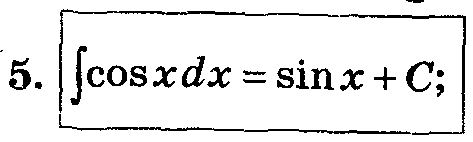
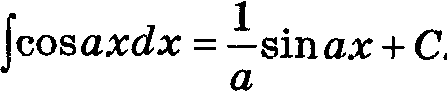
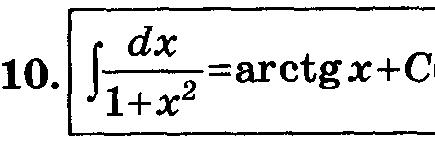
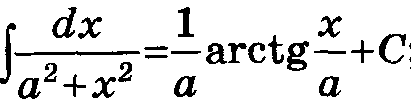
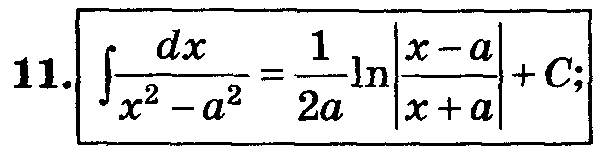
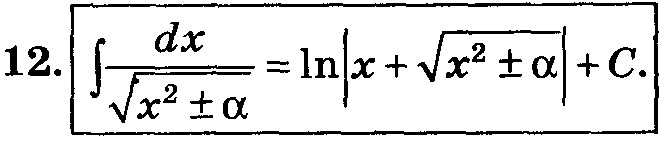
План вычисления площади криволинейной трапеции:
1. Схематический чертеж.
2. Представление искомой площади как суммы или разности площадей.
3. Записать каждую функцию в виде y = f(x).
4. Вычислить площадь каждой криволинейной трапеции или площади искомой фигуры.
Площади фигур.
у у
S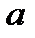 
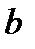х
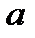
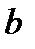х S
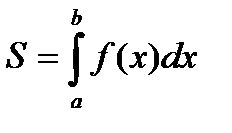
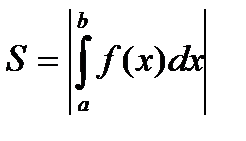
Если рассмотренная фигура не является криволинейной трапецией, тогда площадь нужно представить как сумму или разность криволинейных трапеций.
m
n
S1 S2
a b
S = S1 + S2 S = S amb – S anb
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО ВЫПОЛНЕНИЯ СТУДЕНТАМИ:
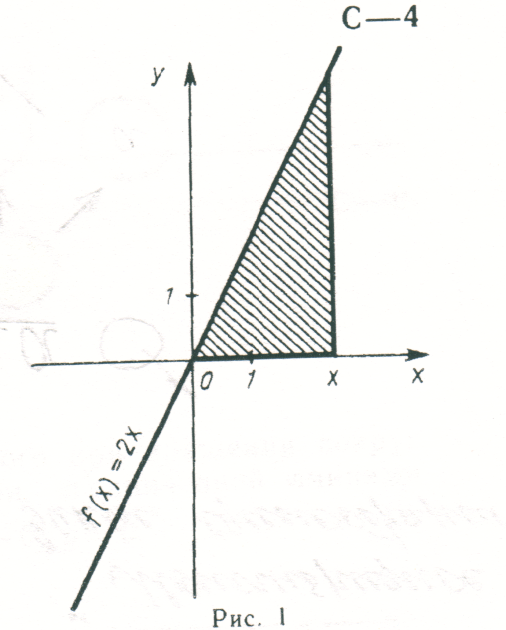
1. Запишите формулу, выражающую площадь S (x) трапеции, заштрихованной на рисунке, как функцию от х.
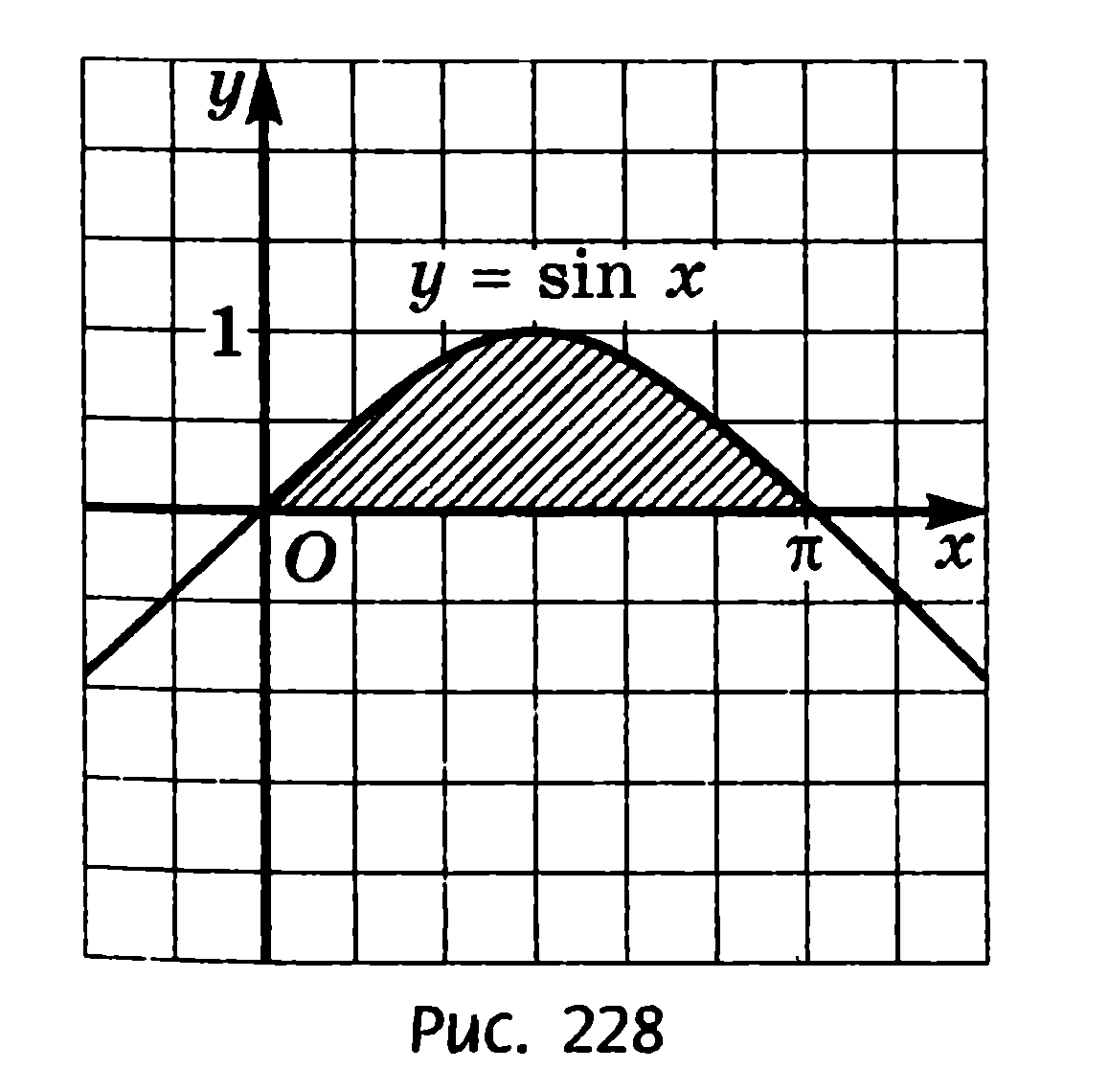
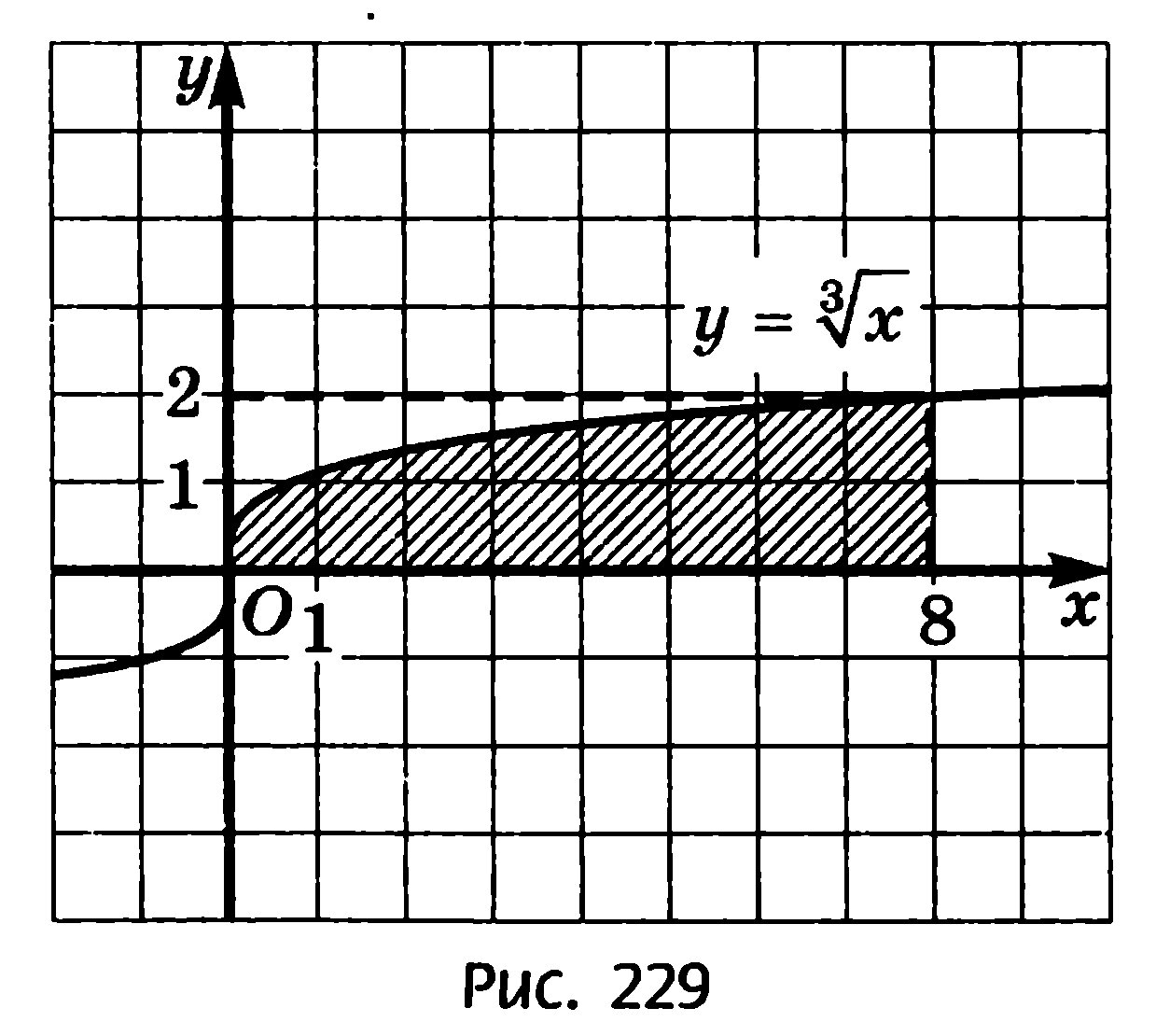
2. Вычислите площадь фигуры, заштрихованной на рисунке:
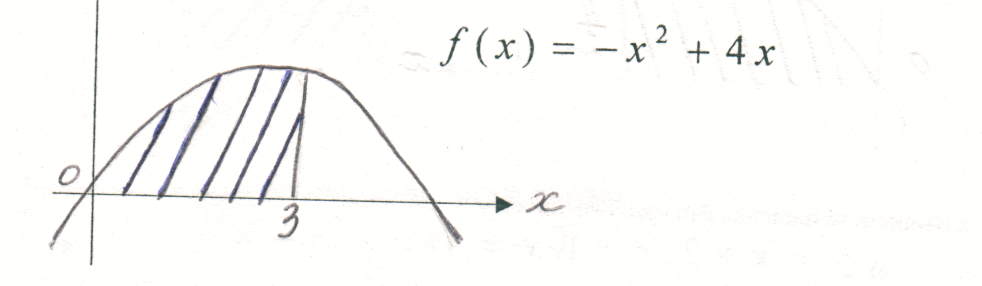
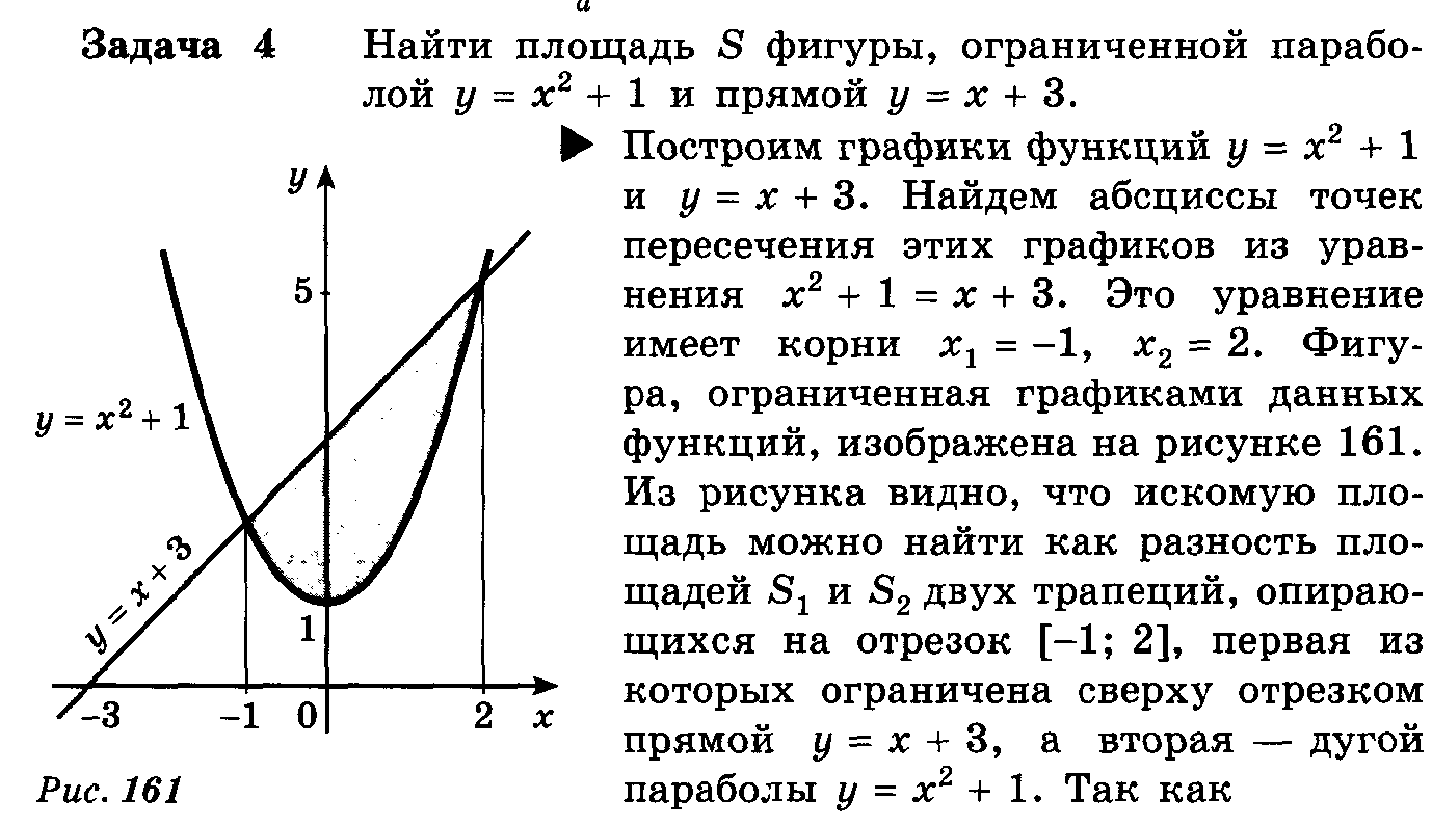
3. Вычислите площадь фигуры, ограниченной линиями:
a.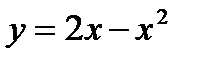 
и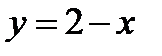 
b. х = - 1, x =2, у = 0 и у = х2 + 1
c. у = 0 и у = 1 – х2
