2020-05-11
79
у = tgx.
Свойства функции y = tgx.
1. Df = (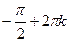
; 
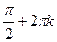), кÎZ.
2. Ef = R.
3. Функция периодическая с периодом p.
При построении графика можно его построить сначала на интервале (
; 
).
4. Функция нечетная.
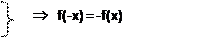f(x) = tgx
f(x) = tg(-x) = -tgx
график функции симметричен относительно начала координат.
Можно начинать построение с промежутка [0;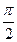 
).
5. Функция непрерывна в любой точке области определения.
Для построения графика функции у = tgx возьмем несколько точек на промежутке [0; 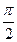) и построим график у = tgx на этом промежутке.
 |
Выполнив последовательно симметрию относительно начала координат и параллельные переносы на pк, кÎZ, получим график функции у = tgx (тангенсоиду).
6. Нули функции: х = pк, кÎZ.
7. Функция строго возрастает на (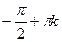
; 
), кÎZ.
у = сtgx.
Т.к. ctgx = - tg(x+ 
), то график функции у = ctgx получается из графика функции у = tgx параллельным переносом вдоль оси абсцисс влево на 
и последующей симметрией относительно оси 0х.
 |
График функции у = ctgx называется котангенсоидой.
Свойства функции y = сtgx.
1. Df = (pk;p+pk), кÎZ.
2. Ef = R.
3. Функция периодическая с периодом p.
4. Функция нечетная.
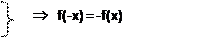f(x) = ctgx
f(x) = ctg(-x) = -ctgx
график функции симметричен относительно начала координат.
5. Функция непрерывна в любой точке области определения.
6. Нули функции: х = , кÎZ.
7. Функция строго убывает на (pk;p+pk), кÎZ.
Напоминаю: кто не сделал??????? Доделать
1. Презентация на тему «Параллельное проектирование».
2. Реферат на тему «Векторное задание прямых и плоскостей в пространстве».
3. Реферат на тему «Жизнь и деятельность Рене Декарта».
