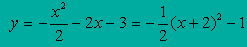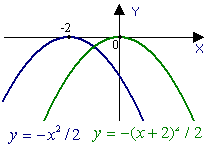Задание: (написать конспект, научиться преобразовывать графики функций)
Преобразования графиков функций — это линейные преобразования функции y = f (x) или её аргумента x к виду y = af (kx + b) + m, а также преобразование с использованием модуля.
| Общий вид функции | Преобразования |
| y = f (x - b) | Параллельный перенос графика вдоль оси абсцисс на | b | единиц · вправо, если b > 0; · влево, если b < 0. |
| y = f (x + b) | · влево, если b > 0; · вправо, если b < 0. |
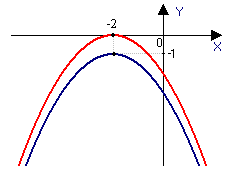
| y = f (x) + m | Параллельный перенос графика вдоль оси ординат на | m | единиц · вверх, если m > 0, · вниз, если m < 0. |
| Отражение графика | |
| y = f (- x) | Симметричное отражение графика относительно оси ординат. |
| y = - f (x) | Симметричное отражение графика относительно оси абсцисс. |
| Сжатие и растяжение графика | |
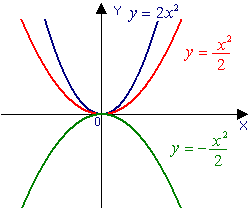
| y = f (kx) | · При k > 1 — сжатие графика к оси ординат в k раз, · при 0 < k < 1 — растяжение графика от оси ординат в k раз. |
| y = kf (x) | · При k > 1 — растяжение графика от оси абсцисс в k раз, · при 0 < k < 1 — cжатие графика к оси абсцисс в k раз. |
| Преобразования графика с модулем | |
| y = | f (x) | | · При f (x) > 0 — график остаётся без изменений, · при f (x) < 0 — график симметрично отражается относительно оси абсцисс. |
| y = f (| x |) | · При x 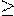 0 — график остаётся без изменений,
· при x < 0 — график симметрично отражается относительно оси ординат. 0 — график остаётся без изменений,
· при x < 0 — график симметрично отражается относительно оси ординат.
|
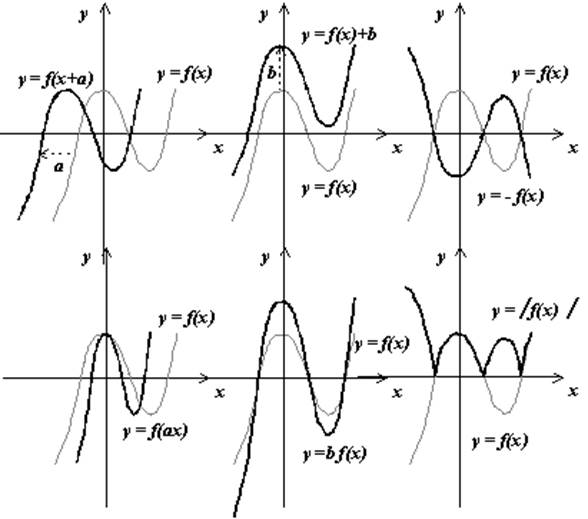
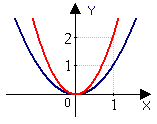
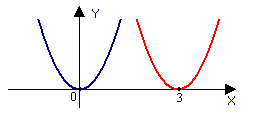
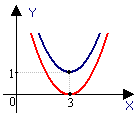
Примеры: 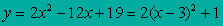
|
Построить графики функций у=х2+4, у=(х-2)2, у=(х+4)2-3, у=-0,5(х+3)2-1
Учебник по алгебре
Тема 2. Степенная функция.
С.39-46 конспект
№119(1,4)
№121(1,3)
№124(1,3,5,7)
Тема 3. Показательная функция.
С. 72-75 конспект
№194(1,2)
№201(1,3)
Тема 4. Логарифмическая функция.
С.100-103 конспект
№321
№322
№324(3,4)
№332(2,4)
Тема 5. Графики и свойства тригонометрических функций у = sinx, y = cosx
Задание: (написать конспект, научиться чертить графики функций)
у = sinx
1. Df = R.
2. Ef = [-1;1].
график функции располагается в полосе, ограниченной прямыми у = -1 и у =1.
3. Функция периодическая с периодом 2p.
4. Функция нечетная.
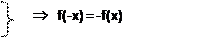 f(x) = sinx
f(x) = sinx
f(x) = sin(-x) = -sinx
график функции симметричен относительно начала координат.
5. Функция непрерывна на всей числовой прямой.
Построим график функции у = sinx.
sinx = 0 [0;p]
х1=0; х2=p;
график функции пересекает в этих точках ось абсцисс.
[0; 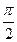 ] - функция возрастает от 0 до 1; [
] - функция возрастает от 0 до 1; [ 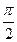 ;p] - функция убывает от 0 до 1.
;p] - функция убывает от 0 до 1.
| х | 0 | 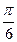
| 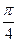
| 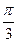
| 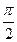
| 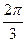
| 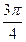
| 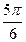
| 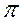
|
| у=sinx | 0 | 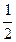
| 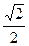
| 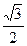
| 1 | 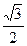
| 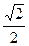
| 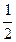
| 0 |
Построим эти точки на координатной плоскости и соединим их плавной линией.
Выполнив последовательно симметрию полученной части графика относительно начала координат (т.к. функция нечетная), а затем параллельные переносы на 2pк, кÎZ (т.к. функция периодическая) получим график функции у=sinx (синусоиду).
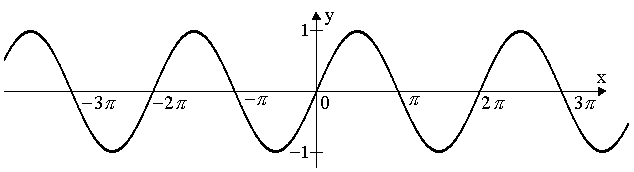
6. Нули функции: х=pк, кÎZ.
7. Функция строго возрастает от -1 до 1 на [ 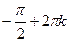 ;
; 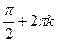 ], кÎZ.
], кÎZ.
Функция строго убывает от 1 до -1 на [ 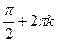 ;
; 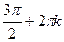 ], кÎZ.
], кÎZ.
8. Функция имеет минимумы, равные -1, в точках х = 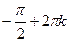 , кÎZ;
, кÎZ;
функция имеет максимумы, равные 1, в точках х = 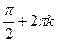 , кÎZ.
, кÎZ.
y = cosx
Т.к. cosx = sin(x+ 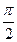 ) для любого хÎR, то график функции у = cosx, хÎR, получается из графика функции у = sinх, хÎR, смещением вдоль оси абсцисс влево на отрезок длиной
) для любого хÎR, то график функции у = cosx, хÎR, получается из графика функции у = sinх, хÎR, смещением вдоль оси абсцисс влево на отрезок длиной 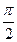 .
.
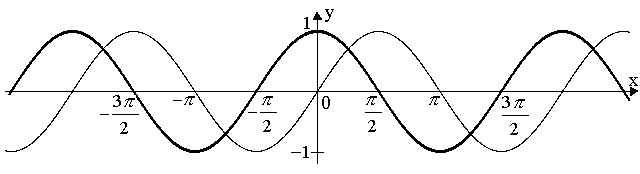 |
Следовательно, графиком косинуса будет смещенная синусоида, называемая косинусоидой.
Свойства функции y = cosx.
1. Df = R.
2. Ef = [-1;1].
3. Функция периодическая с периодом 2p.
4. Функция четная.
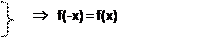 f(x) = соsx
f(x) = соsx
f(x) = соs(-x) = соsx
график функции симметричен относительно оси 0у.
5. Функция непрерывна в любой точке х0ÎR.
6. Нули функции: х = 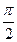 +pк, кÎZ.
+pк, кÎZ.
7. Функция строго возрастает от -1 до 1 на [ 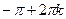 ;
; 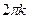 ], кÎZ.
], кÎZ.
Функция строго убывает от 1 до -1 на [ 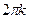 ;
; 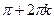 ], кÎZ.
], кÎZ.
8. Функция имеет минимумы, равные -1, в точках х = p+2pк, кÎZ;
функция имеет максимумы, равные 1, в точках х =2pк, кÎZ.
Тема 6. Графики и свойства тригонометрических функций y = tgx, у = сtgx.(написать конспект)
 2020-05-11
2020-05-11 155
155