Волгодонский инженерно-технический институт - филиал НИЯУ МИФИ
КУРС ЛЕКЦИЙ
По дисциплине «Математический анализ» 2 семестр
Для студентов очной формы обучения
Раздел №1 «Приложения производной»
Волгодонск
Теоремы о дифференцируемых функциях.
Теорема Ферма.
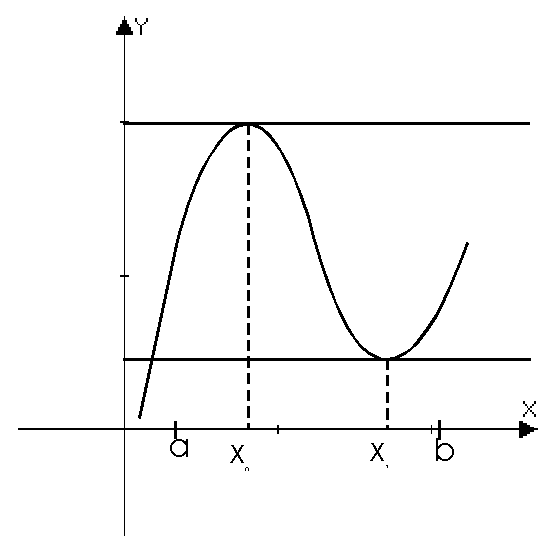 Пусть функция
Пусть функция 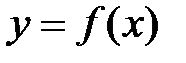 определена и дифференцируема
определена и дифференцируема
на интервале (a;b) и в некоторой точке x0 этого интервала принимает наибольшее или наименьшее значение. Тогда 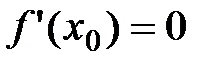 .
.
Доказательство:
По определению производной:
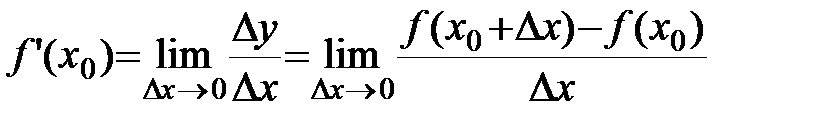 .
.
Пусть для определенности в точке 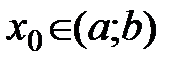 функция
функция 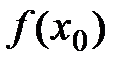 принимает набольшее значение. Тогда числитель
принимает набольшее значение. Тогда числитель 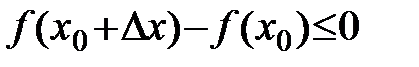 .
.
Рассмотрим два случая:
1) 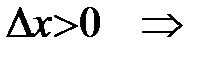
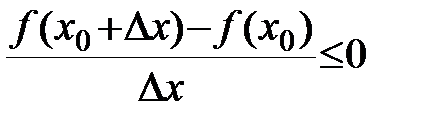 .
.
По теореме о предельном переходе в неравенствах: предел дроби меньше нуля Þ 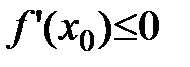 .
.
2) 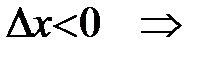
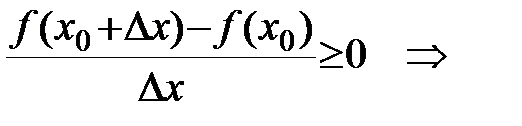
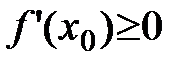 .
.
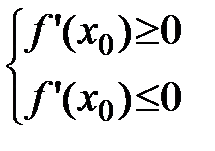
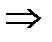
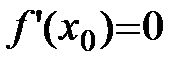 .
.
Ч.т.д.
Геометрический смысл теоремы Ферма:
Так как 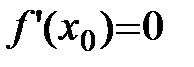 , то угловой коэффициент касательной равен нулю
, то угловой коэффициент касательной равен нулю 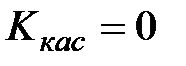 Þ касательная параллельна оси ОХ.
Þ касательная параллельна оси ОХ.
Теорема Ролля.
Пусть функция 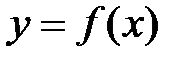 определена и непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), причем на концах интервала принимает одинаковые значения
определена и непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), причем на концах интервала принимает одинаковые значения 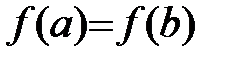 . Тогда существует точка сÎ(a;b), значения производной в которой равно 0, т.е.
. Тогда существует точка сÎ(a;b), значения производной в которой равно 0, т.е. 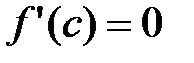 .
.
Доказательство:
| 0 |
| b |
| a |
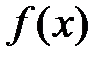 непрерывна на отрезке [a;b], то по II-й т. Вейерштрасса о непрерывных функциях
непрерывна на отрезке [a;b], то по II-й т. Вейерштрасса о непрерывных функциях 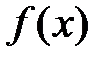 принимает на [a;b] наибольшее М и наименьшее m значения. y
принимает на [a;b] наибольшее М и наименьшее m значения. y
Возможны два случая:
1) М=m.
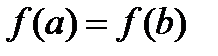
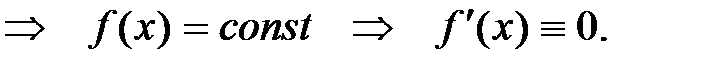
| 0 |
| b |
| a |
| x |
| M |
| m |
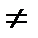 m.
m.
y
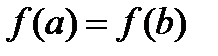
Хотя бы одна из точек, в которых функция принимает наибольшее или наименьшее значения, находится внутри [a;b].
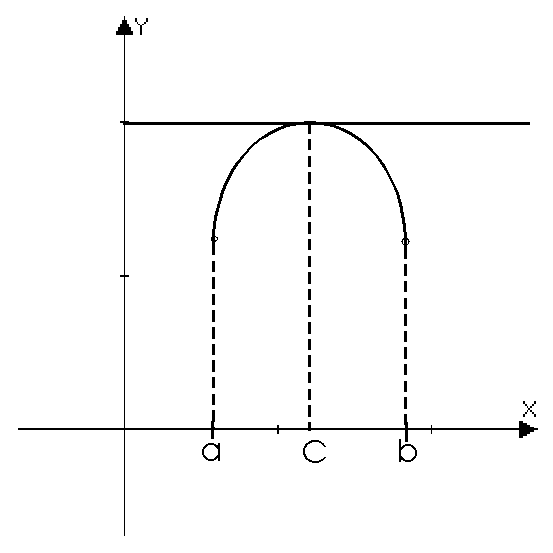 В этом случае в указанной точке выполняются условия теоремы Ферма и, следовательно, существует точка c, принадлежащая (a;b), в которой производная
В этом случае в указанной точке выполняются условия теоремы Ферма и, следовательно, существует точка c, принадлежащая (a;b), в которой производная 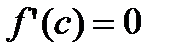 .
.
Ч.т.д.
Геометрический смысл теоремы Ролля:
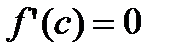 Þ Ккас=0 Þ касательная
Þ Ккас=0 Þ касательная
в точке c параллельна оси ОX.
Теорема Лагранжа.
Пусть функция 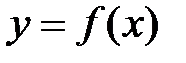 определена и непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Тогда существует точка cÎ(a;b), значение производной в которой равно
определена и непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Тогда существует точка cÎ(a;b), значение производной в которой равно 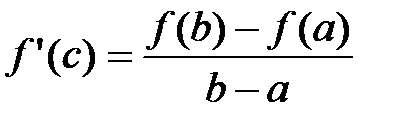 .
.
Доказательство:
Введем вспомогательную функцию 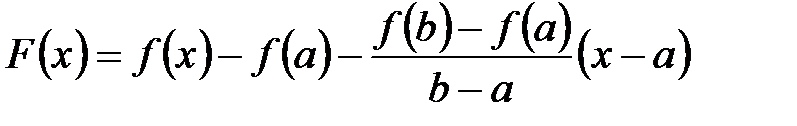 .
.
Эта функция непрерывна и дифференцируема как сумма непрерывных и дифференцируемых функций.
| Итак, для F(x) выполняются все условия теоремы Ролля. |
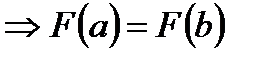
|

Þ существует точка сÎ(a;b) такая, что 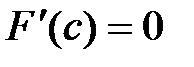 .
.
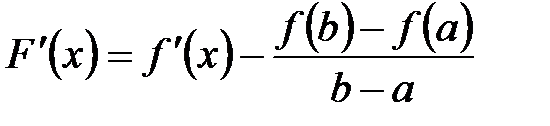 .
.
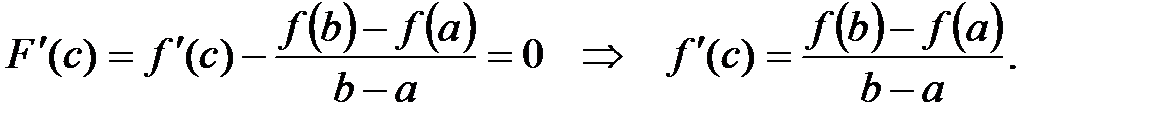
Ч.т.д.
Геометрический смысл теоремы Лагранжа:
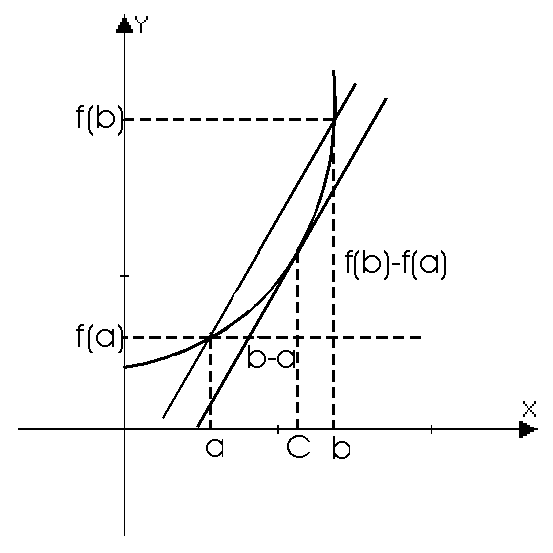
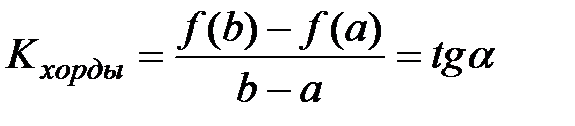 .
.
Существует точка cÎ(a;b), в которой угловой коэффициент касательной равен угловому коэффициенту хорды, соединяющей граничные точки:
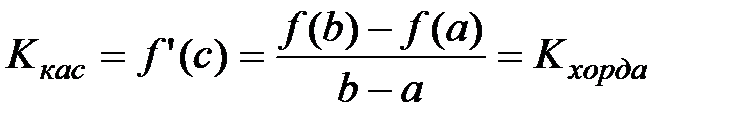 .
.
Найдется такая точка на графике, касательная в которой параллельна хорде, стягивающей концы отрезка [a;b].
Теорема Коши.
Пусть функции f(x) и g(x) определены и непрерывны на отрезке [a;b] и дифференцируемы на интервале (a;b), причем производная функции g(x) отлична от нуля, g¢(x)¹0. Тогда существует такая точка cÎ(a;b), для которой выполняется равенство: 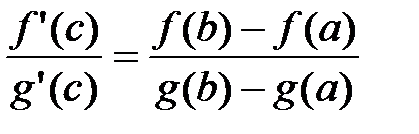 .
.
Доказательство:
Рассмотрим вспомогательную функцию:
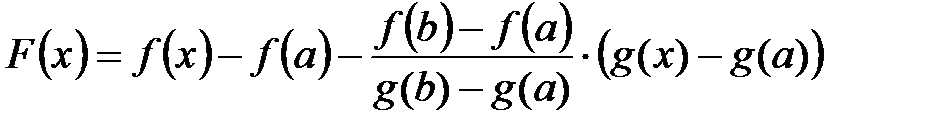 .
.
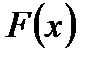 непрерывна и дифференцируема как сумма непрерывных и дифференцируемых функций.
непрерывна и дифференцируема как сумма непрерывных и дифференцируемых функций.
Итак, для F(x) выполняются все условия теоремы Ролля. 
|
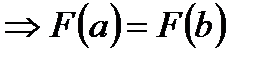
|

Þ существует точка сÎ(a;b): 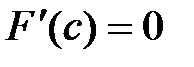 .
.
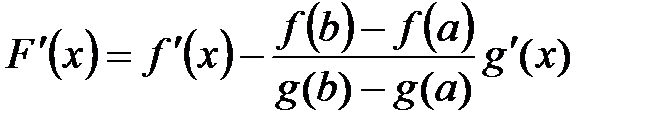 ;
; 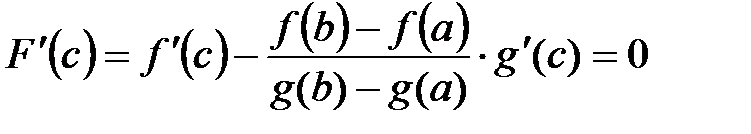 .
.
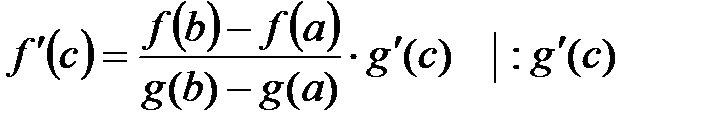 .
.
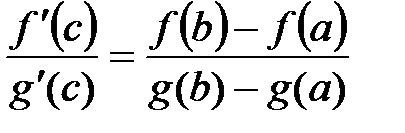 .
.
Ч.т.д.
Правило Лопиталя.
Теорема.
Пусть функции f(x) и g(x) определены и дифференцируемы в некоторой окрестности точки x0, за исключением может быть самой точки x0, и 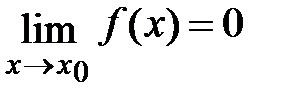 ,
, 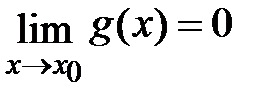 . Тогда если существует предел отношения производных функций
. Тогда если существует предел отношения производных функций 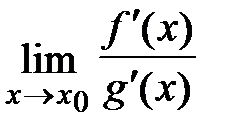 , то существует предел отношения самих функций
, то существует предел отношения самих функций 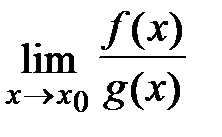 , причем они равны между собой, т.е.
, причем они равны между собой, т.е. 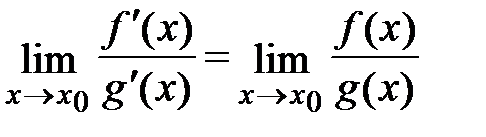 .
.
Доказательство:
Доопределим f(x) и g(x) в точке x0, положив
f(x0) = g(x0) = 0.
В окрестности точки x0, т.е. на (x0,х) для функций f(x) и g(x) выполняются условия теоремы Коши. Следовательно, существует точка сÎ(x0, х) такая, что
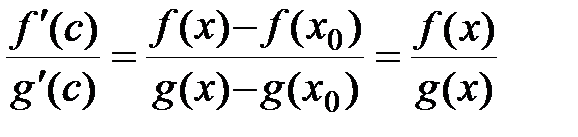 , т.к. f(x0) = g(x0) = 0.
, т.к. f(x0) = g(x0) = 0.
Перейдем к пределу при x 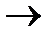 x0
x0 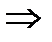 с
с 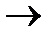 x0:
x0:
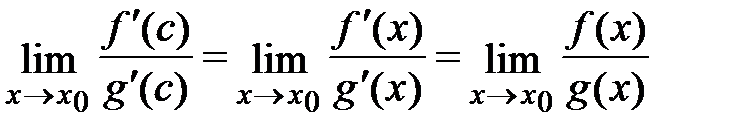 .
.
Ч.т.д.
Замечание. На практике при раскрытии неопределенности типа 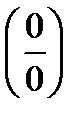 можно пользоваться правилом Лопиталя и в случаях, когда x®±¥, x®¥.
можно пользоваться правилом Лопиталя и в случаях, когда x®±¥, x®¥.
Для раскрытия неопределенностей типа 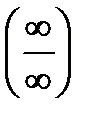 существует аналог правила Лопиталя.
существует аналог правила Лопиталя.
Теорема.
Пусть функции f(x) и g(x) непрерывны и дифференцируемы в некоторой окрестности точки x0, за исключением самой точки x0, причем 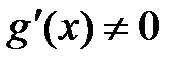 . Пусть
. Пусть 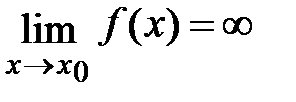 ,
, 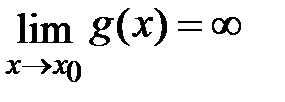 . Тогда если существует предел отношения производных функций
. Тогда если существует предел отношения производных функций 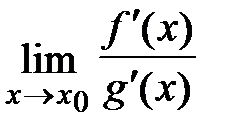 , то существует предел отношения самих функций
, то существует предел отношения самих функций 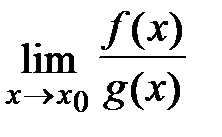 , причем они равны между собой, т.е.
, причем они равны между собой, т.е. 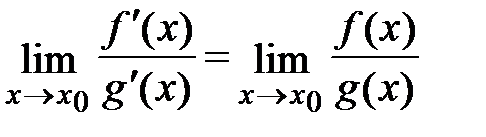 .
.
В дальнейшем это утверждение будем также называть правилом Лопиталя.
Замечание 1. Правилом Лопиталя можно пользоваться при раскрытии неопределенностей вида (¥-¥), (0×¥), (1¥), (¥0), (00), сводя их к неопределенностям типа 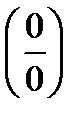 ,
, 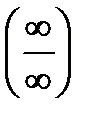 .
.
Замечание 2. Если после применения правила Лопиталя опять получаем неопределенность вида 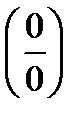 или
или 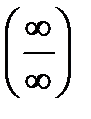 , то его можно применить повторно.
, то его можно применить повторно.
Пример: Вычислить пределы по правилу Лопиталя.
1. Чтобы применять правило Лопиталя при неопределенности вида 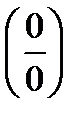 или
или 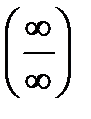 , нужно продифференцировать отдельно числитель и знаменатель дроби, и вычислить полученный предел.
, нужно продифференцировать отдельно числитель и знаменатель дроби, и вычислить полученный предел.
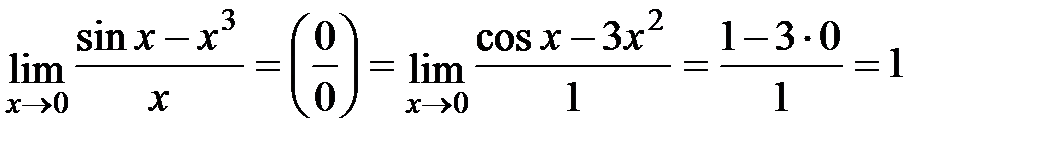 .
.
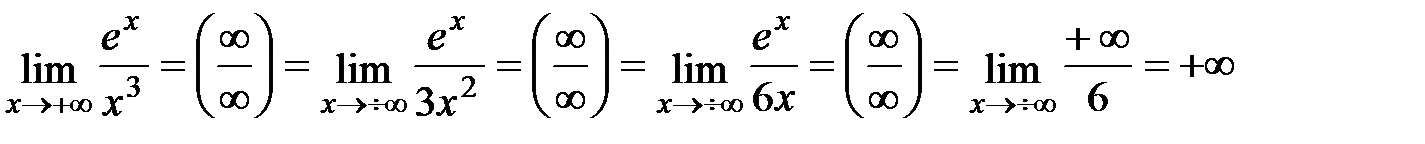 .
.
Вывод: показательная функция (y=an) всегда растет быстрее, чем степенная (у=xn).
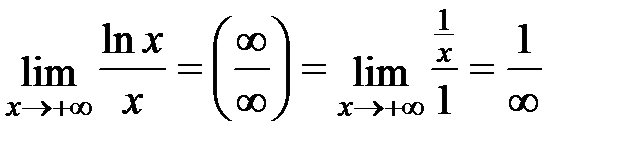 .
.
Вывод: логарифмическая функция (y=logax) растет медленнее, чем степенная.
2. Неопределенность вида (0×¥) нужно преобразовать в неопределенность вида 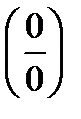 или
или 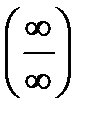 , опустив один из множителей в знаменатель в отрицательной степени, и потом применять правило Лопиталя.
, опустив один из множителей в знаменатель в отрицательной степени, и потом применять правило Лопиталя.
3. При показательной неопределенности: (00), (1¥), (¥0); прежде чем применять правило Лопиталя, нужно прологарифмировать этот предел по основанию e.
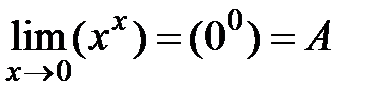 .
.
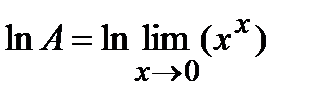 =
= 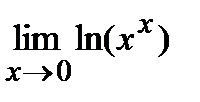 =
= 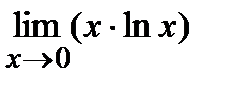 =(0×¥)=
=(0×¥)= 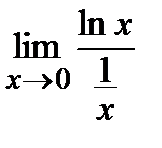 =
= 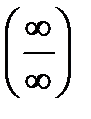 =
= 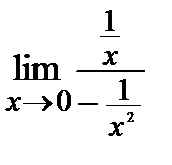 =
=
= 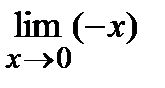 =0;
=0;
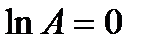 Þ A=e0=1.
Þ A=e0=1.
Формулы Тейлора и Маклорена.
Пусть функция 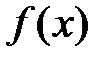 n раз дифференцируема в окрестности точки x0.Найдем многочлен
n раз дифференцируема в окрестности точки x0.Найдем многочлен 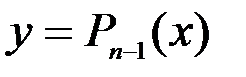 степени не выше n-1, такой что
степени не выше n-1, такой что
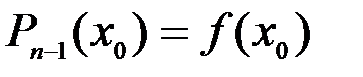 ,
, 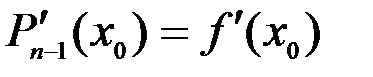 ,,…,
,,…, 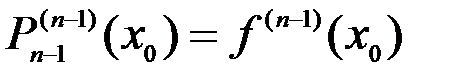 .
.
Такой многочлен в некотором смысле «близок» к функции 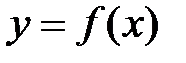 .
.
Будем искать этот многочлен в форме многочлена, разложенного по степеням 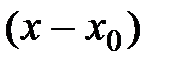 , с неопределенными коэффициентами:
, с неопределенными коэффициентами:
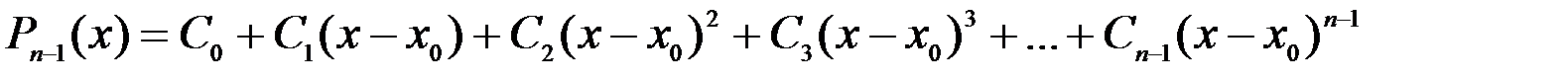 .
.
Неопределенные коэффициенты 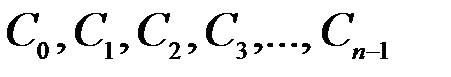 определим так, чтобы выполнялись перечисленные выше условия.
определим так, чтобы выполнялись перечисленные выше условия.
Найдем производные от 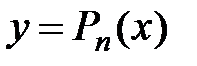 :
:
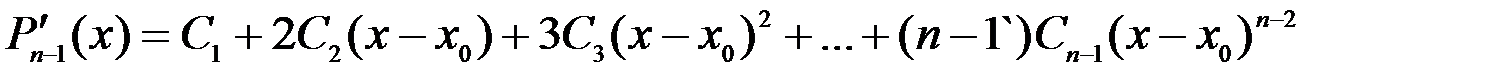 ;
;
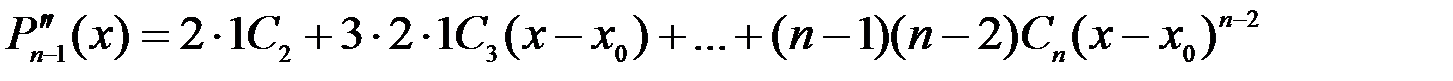 ;…
;…
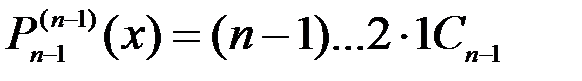 .
.
Подставляя 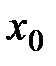 вместо
вместо 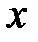 , находим:
, находим:
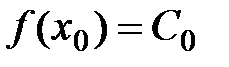 ,
, 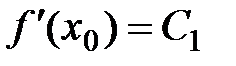 ,
, 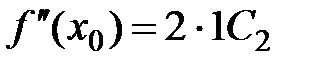 ,
, 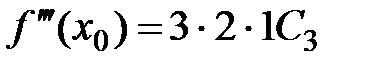 , …,
, …, 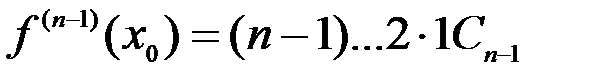 . Отсюда
. Отсюда
Þ 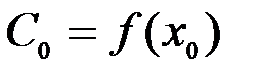 ,
, 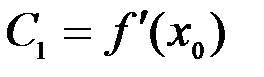 ,
, 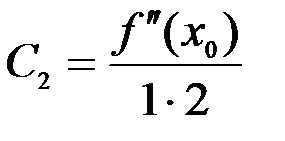 ,
, 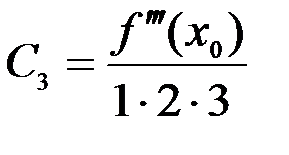 ,…,
,…, 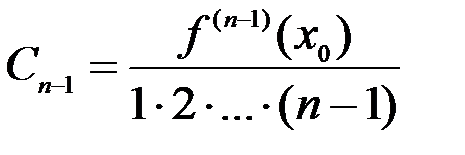 .
.
Искомый многочлен будет иметь вид:
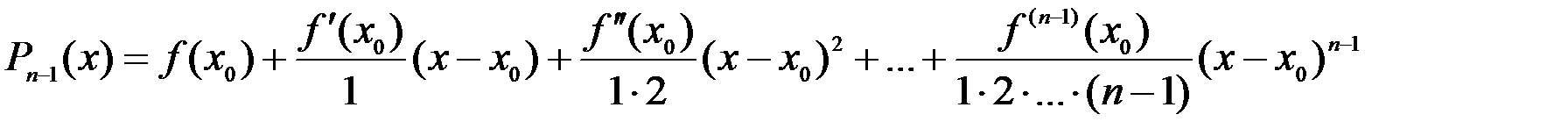 , или
, или
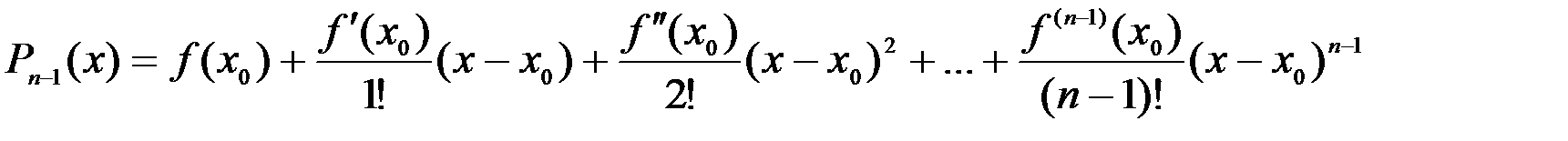 .
.
Этот многочлен мы будем называть многочленом Тейлора.
Теорема. Пусть функция 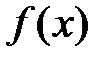 n раз дифференцируема в окрестности точки x0. Тогда в этой окрестности для функции
n раз дифференцируема в окрестности точки x0. Тогда в этой окрестности для функции 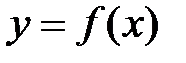 справедлива следующая формула Тейлора:
справедлива следующая формула Тейлора:
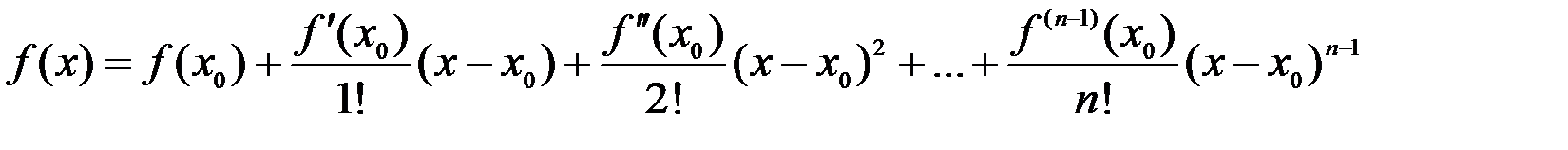 +
+
+ 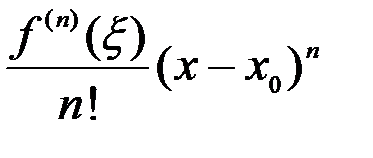 .
.
Здесь 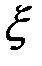 некоторая точка, заключенная между
некоторая точка, заключенная между 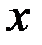 и
и 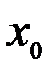 (
(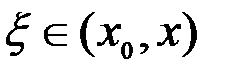 ), зависящая от
), зависящая от 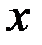 , а
, а 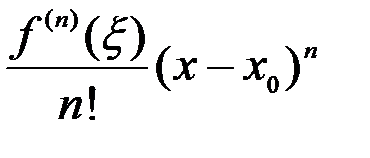 =
= 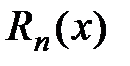 - остаточный член в форме Лагранжа.
- остаточный член в форме Лагранжа.
Доказательство:
Обозначим через 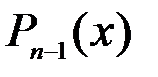 многочлен
многочлен
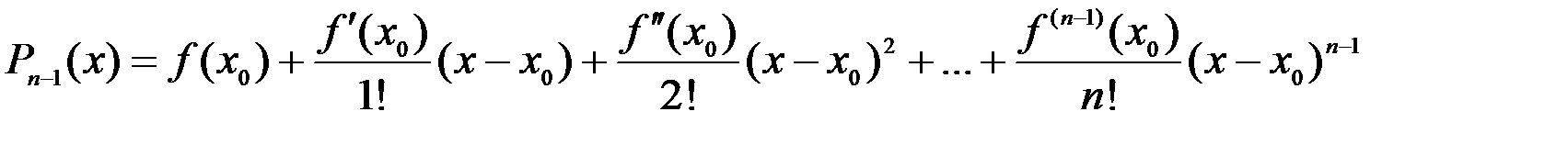 .
.
Ясно, что для каждого выбранного 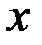 существует такое число
существует такое число 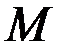 , для которого будет выполняться равенство:
, для которого будет выполняться равенство:
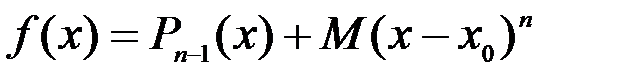 . (1)
. (1)
Покажем, что это число 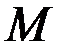 при уже выбранном
при уже выбранном 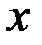 будет равно
будет равно 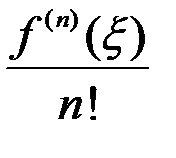 при некотором
при некотором 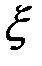 из промежутка
из промежутка 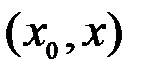 .
.
Определим функцию
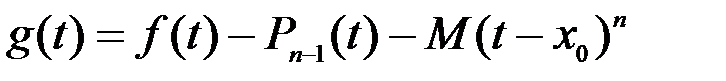 .
.
Ясно, что
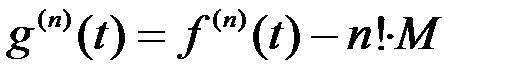
Следовательно, доказательство мы закончим, если покажем, что в некоторой точке 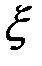 (
(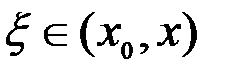 ) будет выполняться равенство:
) будет выполняться равенство: 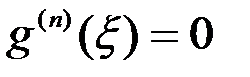 .
.
Непосредственными вычислениями проверяется (см. многочлен Тейлора!), что для всех 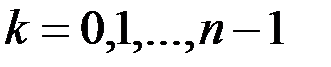 выполняются равенства:
выполняются равенства:
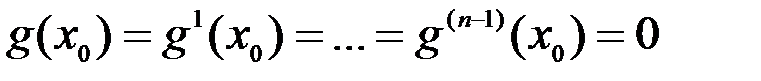 (2)
(2)
Число 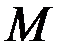 выбрано таким образом, чтобы выполнялось равенство (1) и, следовательно,
выбрано таким образом, чтобы выполнялось равенство (1) и, следовательно, 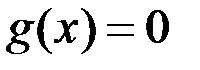 . Таким образом, для функции
. Таким образом, для функции 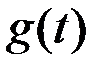 на промежутке
на промежутке
[ 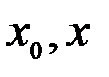 ] выполняются все условия теоремы Ролля. Следовательно, на интервале (
] выполняются все условия теоремы Ролля. Следовательно, на интервале (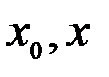 ) существует такая точка
) существует такая точка 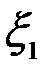 , производная функции
, производная функции 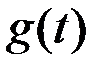 , в которой равна нулю, то есть
, в которой равна нулю, то есть 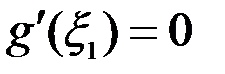 . Но тогда с учетом (2) теорему Ролля можно применить к функции
. Но тогда с учетом (2) теорему Ролля можно применить к функции 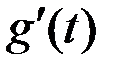 на промежутке [
на промежутке [ 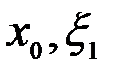 ] и так далее. Применяя, в конце концов, теорему Ролля к функции
] и так далее. Применяя, в конце концов, теорему Ролля к функции 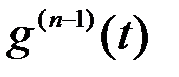 на соответствующем промежутке, получим точку
на соответствующем промежутке, получим точку 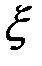 , для которой будет справедливо равенство
, для которой будет справедливо равенство 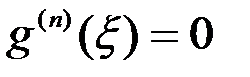 .
.
Утверждение доказано.
Если x0=0, то формула Тейлора превращается в формулу Маклорена:
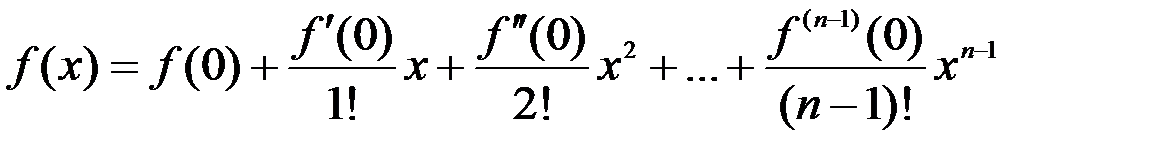 +
+ 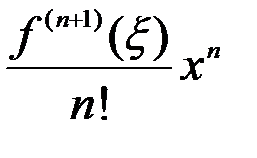
Заметим, что числа n могут выбираться различными, в зависимости и от наличия у функции производных соответствующего порядка, и от необходимой точности расчетов. Например, формула Тейлора для n=4 будет иметь вид:
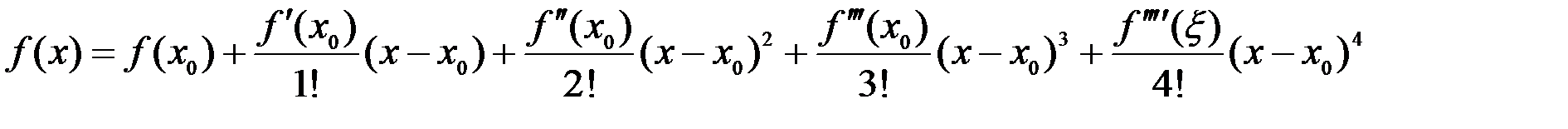
Разложение некоторых элементарных функций по формуле Маклорена.
1. 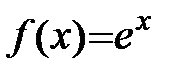 .
.
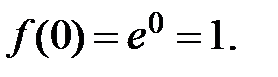
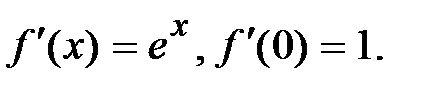
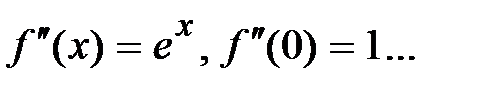
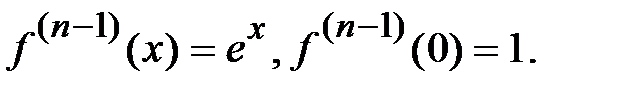
Þ 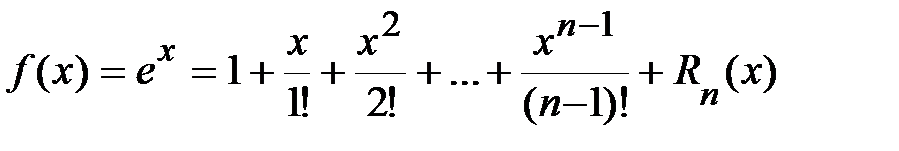 ,
,
где 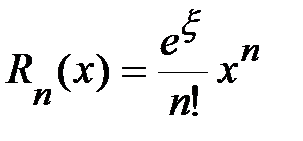 .
.
2. 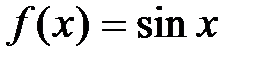 .
.
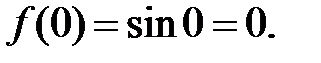
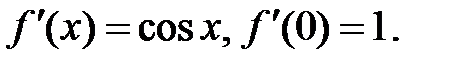
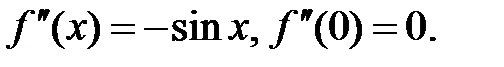
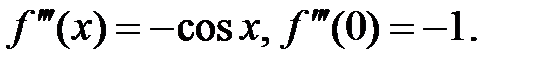
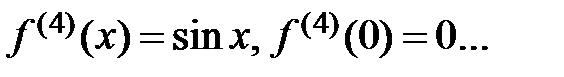
Þ 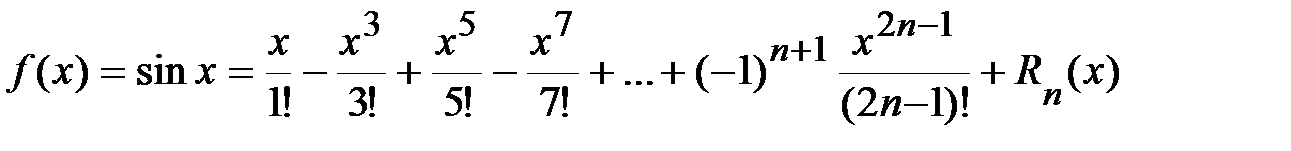 ,
,
где 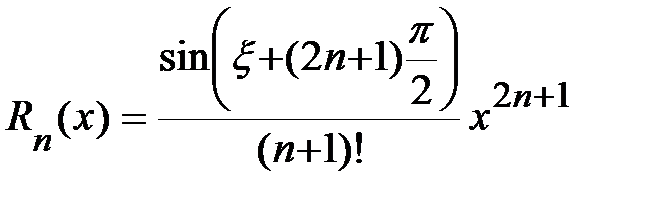 .
.
3. 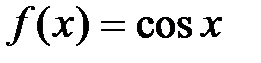 .
.
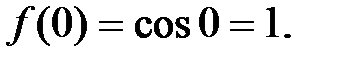
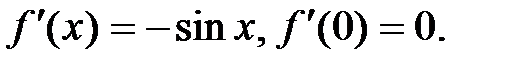
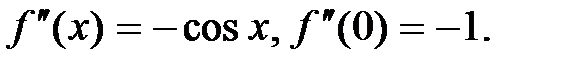
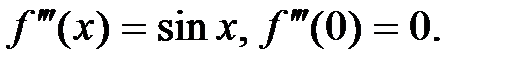
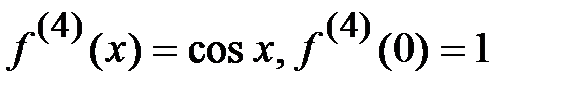 ,…
,…
Þ 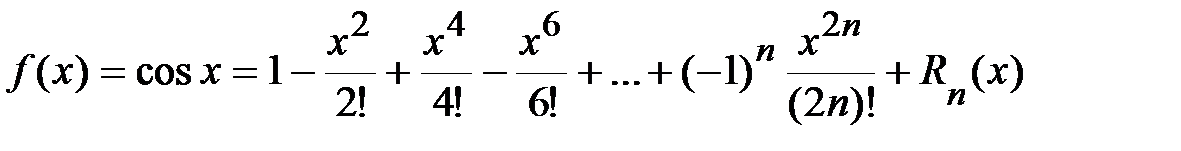 ,
,
где 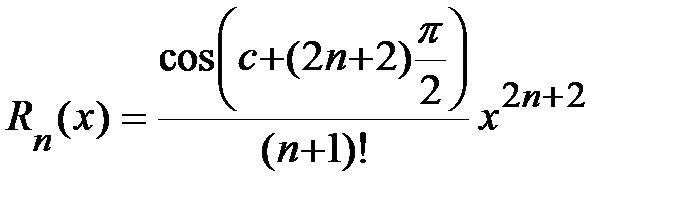 .
.
Пример:
Разложить функцию 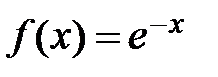 по формуле Маклорена, взяв 4 слагаемых.
по формуле Маклорена, взяв 4 слагаемых.
Воспользуемся формулой Маклорена для функции 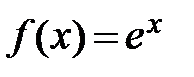 , заменив x на
, заменив x на
(-x):
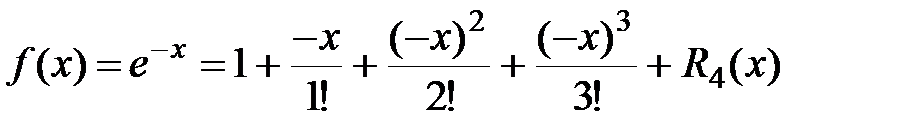 .
.
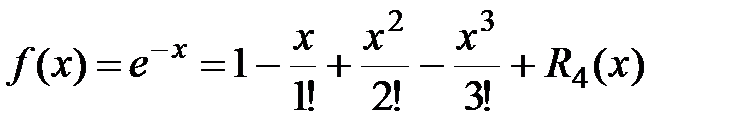 .
.
Приложения формул Тейлора и Маклорена.
Формулы Тейлора и Маклорена имеют широчайшее применение, как для приближенного вычисления значений целого ряда табулированных функций таких, например, как 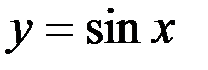 ,
, 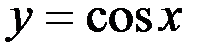 ,
, 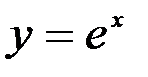 и др., так и для замены сложных функций при решении практических задач многочленами.
и др., так и для замены сложных функций при решении практических задач многочленами.
В качестве примера приложения формулы Маклорена, определим количество членов в разложении функции 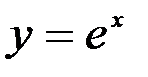 по указанной формуле для вычисления ее значения с точностью до 0.001 при любом x из промежутка [-1,1].
по указанной формуле для вычисления ее значения с точностью до 0.001 при любом x из промежутка [-1,1].
Поскольку 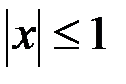 , то в остаточном члене
, то в остаточном члене 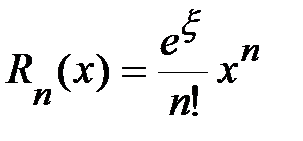 величина
величина 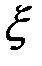 удовлетворяет неравенству:
удовлетворяет неравенству: 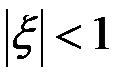 . Следовательно,
. Следовательно,
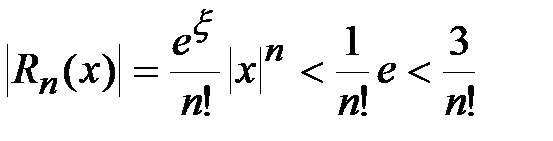 .
.
Очевидно, что если мы заменим на промежутке [-1,1] функцию 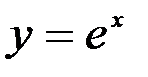 соответствующим многочленом Тейлора, то значения этого многочлена на указанном промежутке будут отличаться от соответствующих значений функции на величину меньшую, чем
соответствующим многочленом Тейлора, то значения этого многочлена на указанном промежутке будут отличаться от соответствующих значений функции на величину меньшую, чем 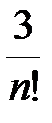 . Выбирая n из условия
. Выбирая n из условия 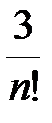 <0.001, мы получим, что
<0.001, мы получим, что 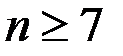 , поскольку (
, поскольку (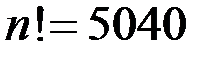 ).
).
Отметим, что формула Тейлора может использоваться и при вычислении пределов.
Признаки монотонности функции.
Пусть функция 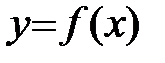 определена и непрерывна на промежутке (a;b).
определена и непрерывна на промежутке (a;b).
Определение: Функция 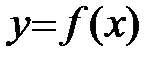 называется неубывающей (невозрастающей) на (a;b), если для любых x1<x2, принадлежащих (a;b), выполняется
называется неубывающей (невозрастающей) на (a;b), если для любых x1<x2, принадлежащих (a;b), выполняется 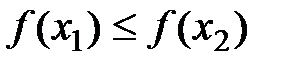 (
(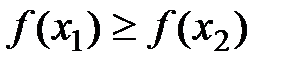 ).
).
Определение: Функция 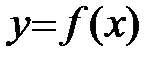 называется возрастающей (убывающей) на (a;b), если для любых x1<x2, принадлежащих (a;b), выполняется
называется возрастающей (убывающей) на (a;b), если для любых x1<x2, принадлежащих (a;b), выполняется 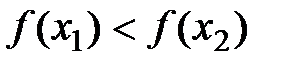 (
(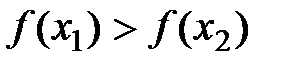 ).
).
Теорема 1.
Для того чтобы функция 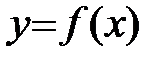 , дифференцируемая на (a;b), была возрастающей, необходимо, чтобы производная на этом промежутке была неотрицательна, т.е.
, дифференцируемая на (a;b), была возрастающей, необходимо, чтобы производная на этом промежутке была неотрицательна, т.е. 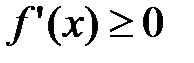 , и достаточно, чтобы
, и достаточно, чтобы 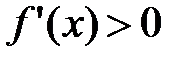 .
.
Доказательство:
Необходимость.
Пусть f(x) возрастает на (a;b). Тогда для любых 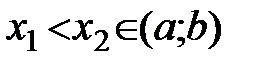 выполняется
выполняется 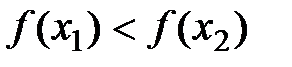 .
.
Þ 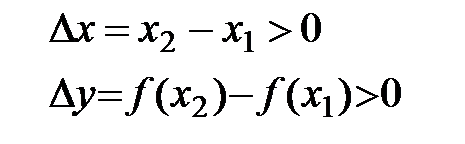 Þ
Þ 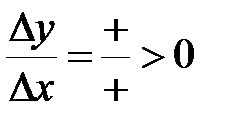 .
.
По определению производной: 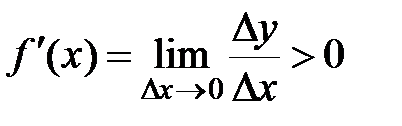 .
.
Достаточность.
Пусть 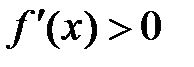 на (a;b). f(x) дифференцируема на (a;b). Выберем на этом промежутке 2 точки х1; х2.
на (a;b). f(x) дифференцируема на (a;b). Выберем на этом промежутке 2 точки х1; х2.
Тогда на (х1; х2) выполняется условие теоремы Лагранжа:
существует точка с Î(х1; х2) такая, что 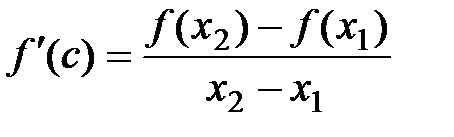 .
.
Þ 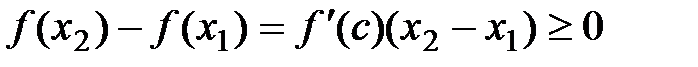 (т.к.
(т.к. 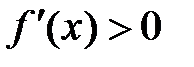 ).
).
Þ 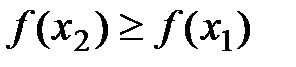 . Þ
. Þ 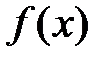 возрастает на (a;b).
возрастает на (a;b).
Ч.т.д.
Теорема 2.
Для того чтобы функция 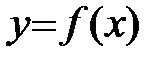 , дифференцируемая на (a;b), была убывающей, необходимо, чтобы производная на этом промежутке
, дифференцируемая на (a;b), была убывающей, необходимо, чтобы производная на этом промежутке 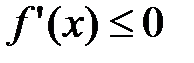 и достаточно, чтобы
и достаточно, чтобы 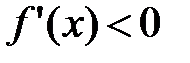 .
.
Доказательство проводится аналогично.
Пример: Найти интервалы возрастания и убывания функции 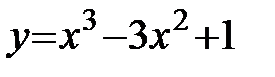 .
.
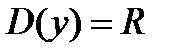 .
.

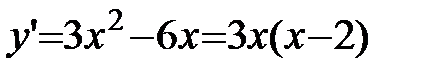 .
.
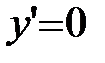 Þ
Þ 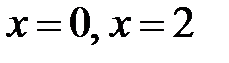 .
.
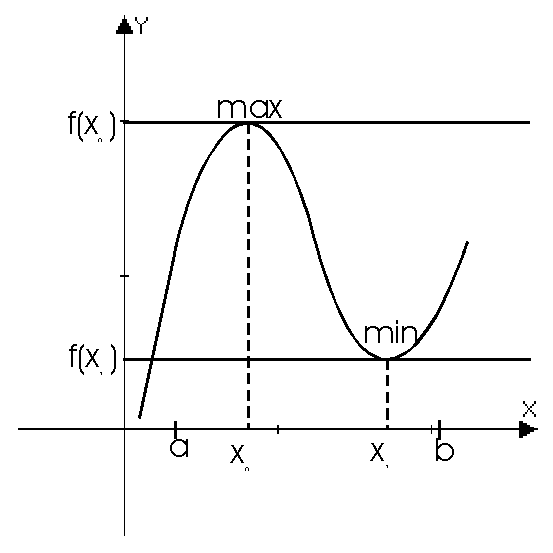 Экстремум функции.
Экстремум функции.
Пусть функция 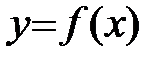 определена в окрестности точки x0.
определена в окрестности точки x0.
Определение: Точка x0 называется точкой строгого локального максимума, если существует такая ее окрестность точки, в которой выполняется неравенство 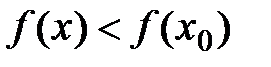 .
.
x0 — max.
Определение: Точка x0 называется точкой строгого локального минимума, если существует такая ее окрестность точки, в которой выполняется неравенство 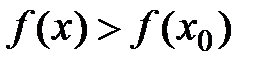 .
.
x0 — min.
Точки локального максимума и минимума называются точками экстремума.
Необходимое условие экстремума дифференцируемой функции.
Если функция 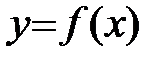 , дифференцируемая в точке x0, имеет в этой точке экстремум, то производная
, дифференцируемая в точке x0, имеет в этой точке экстремум, то производная 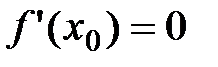 .
.
Доказательство:
Пусть для определенности точка x0 — max.
Тогда по определению существует такая ее окрестность 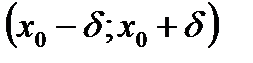 , в которой выполняется неравенство
, в которой выполняется неравенство 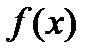 <
< 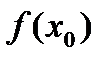 .
.
Т.о. на интервале 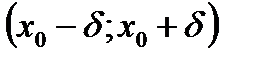 в точке x0 функция принимает наибольшее значение
в точке x0 функция принимает наибольшее значение 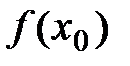 .
.
Тогда по теореме Ферма: 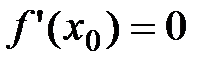 .
.
Аналогично доказывается для минимума функции.
Ч.т.д.
Однако, возможна ситуация, когда функция 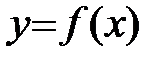 будет иметь экстремум в точке x0 в том случае, когда производная
будет иметь экстремум в точке x0 в том случае, когда производная 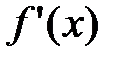 не существует.
не существует.
Точки, в которых производная 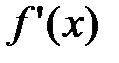 либо равна 0, либо не существует, называются критическими точками производной.
либо равна 0, либо не существует, называются критическими точками производной.
Замечание 1: Обратное утверждение не верно. Не всякая функция, производная которой в точке равна нулю или не существует, имеет в этой точке экстремум.
Замечание 2. Функция имеет экстремум только в критических точках.
Достаточное условие экстремума.
Пусть функция определена в критической точке x0 и дифференцируема в некоторой окрестности этой точки, за исключением, может быть, самой x0. Если «при переходе» через точку x0 слева направо производная меняет знак с плюса на минус, то x0 – точка максимума; с минуса на плюс – точка минимума.

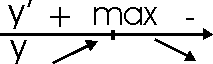
Доказательство:
Пусть производная меняет знак с «+» на «-».
Тогда слева от х0, т.е. на (х0-δ,х0) 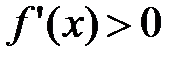 .
.
| y |
| x |
| 0 |
| x0 |
| f(x0) |
| x0+d |
| x0-d |
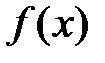 возрастает.
возрастает.
Справа от х0, т.е. на (х0, х0+δ) 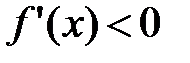 .
.
Þ справа от х0 функция 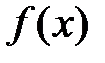 убывает.
убывает.
Т.о. в окрестности точки х0 выполняется
неравенство 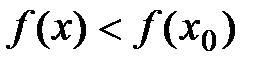 .
.
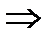 х0 – точка локального максимума.
х0 – точка локального максимума.
Аналогично доказывается для минимума.
Ч.т.д.
Пример: Исследовать функцию на монотонность и найти точки экстремума.
а) 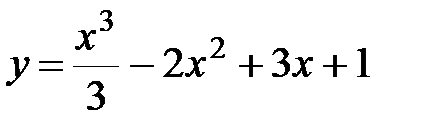 .
.
1. Область определения функции D(y)=R.
2. 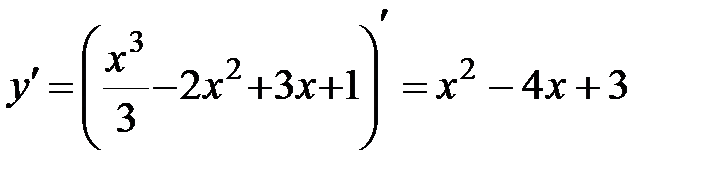 .
.
Критические точки: 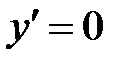 .
. 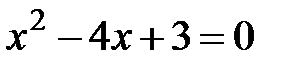 Þ
Þ 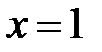 ,
, 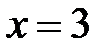 .
.
| x | (-∞;1) | x=1 | (1;3) | x=3 | (3;+∞) |
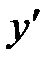
| + | 0 | – | 0 | + |
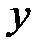
| возрастает | max
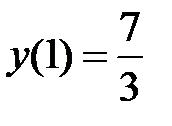
| убывает | min y(3)=1 | возрастает |
б) 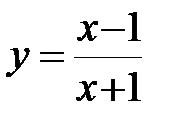 .
.
1. Область определения функции D(y): x¹-1.
2. 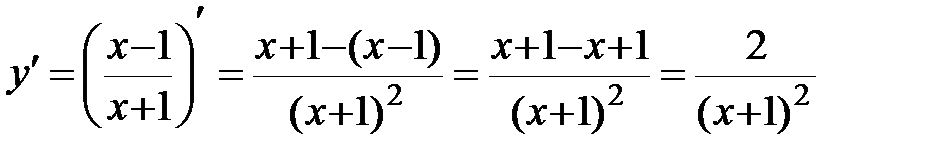 ;
;
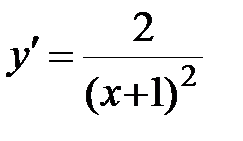 .
.
Критические точки: 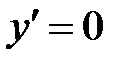 , т.е. числитель равен нулю Þ нет точек;
, т.е. числитель равен нулю Þ нет точек;
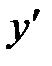 – не существует, т.е. знаменатель равен нулю Þ
– не существует, т.е. знаменатель равен нулю Þ 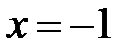 .
.
| x | (-∞;-1) | x=-1 | (-1;+∞) |
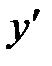
| + | не существует | + |
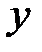
| возрастает | не существует | возрастает |
Точек экстремума нет.
Наибольшее и наименьшее значения функции на отрезке.
Пусть функция 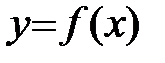 определена и непрерывна на замкнутом промежутке [a;b] и имеет внутри этого промежутка конечную производную.
определена и непрерывна на замкнутом промежутке [a;b] и имеет внутри этого промежутка конечную производную.
Тогда по второй теореме Вейерштрасса она на этом отрезке принимает свои наибольшее и наименьшее значения.
Очевидно, что эти значения могут достигаться либо в критических точках, либо на концах отрезка.
Поэтому для нахождения наибольшего и наименьшего значений функции применяют следующий алгоритм решения:
1. Находим критические точки функции. Отбираем те точки, которые принадлежат данному отрезку.
2. Вычисляем значения функции в найденных точках.
3. Вычисляем значения функции на концах отрезка.
4. Из полученных значений функции выбираем наибольшее и наименьшее.
Исследование функции на максимум и минимум с помощью производной второго порядка.
Пусть функция 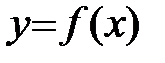 определена и непрерывна на промежутке (a;b).
определена и непрерывна на промежутке (a;b).
Теорема.
Пусть 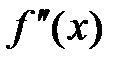 существует и непрерывна в некоторой окрестности точки
существует и непрерывна в некоторой окрестности точки 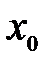 . Пусть
. Пусть 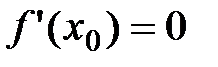 . Если
. Если 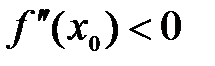 , то в точке
, то в точке 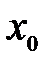 функция имеет максимум; если
функция имеет максимум; если 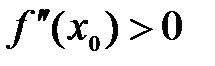 , то в точке
, то в точке 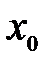 функция имеет минимум.
функция имеет минимум.
Доказательство:
Докажем для максимума.
Пусть 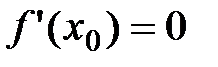 . Пусть
. Пусть 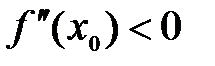 .
.
Так как, по условию, 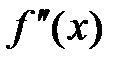 непрерывна в некоторой окрестности точки
непрерывна в некоторой окрестности точки 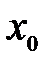 , то найдется некоторая окрестность
, то найдется некоторая окрестность 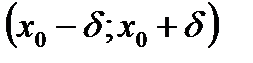 , во всех точках которой вторая производная
, во всех точках которой вторая производная 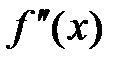 будет отрицательна.
будет отрицательна.
Так как 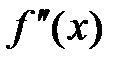 есть производная от первой производной, т.е.
есть производная от первой производной, т.е. 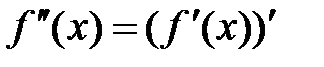 , то из условия
, то из условия 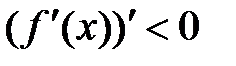 следует, что
следует, что 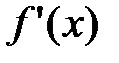 убывает на промежутке, содержащем точку
убывает на промежутке, содержащем точку 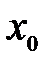 , т.е. в окрестности
, т.е. в окрестности 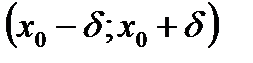 .
.
Так как 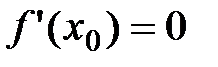 , Тогда слева от
, Тогда слева от 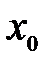 , т.е. на (х0-δ,х0) имеем
, т.е. на (х0-δ,х0) имеем 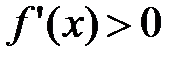 , а справа от
, а справа от 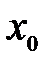 , т.е. на (х0, х0+δ) имеем
, т.е. на (х0, х0+δ) имеем 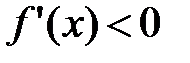 , т.е. производная
, т.е. производная 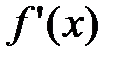 «при переходе» через точку x0 слева направо меняет знак с плюса на минус. А это значит, что точка
«при переходе» через точку x0 слева направо меняет знак с плюса на минус. А это значит, что точка 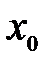 – точка максимума.
– точка максимума.
Аналогично доказывается для минимума.
Ч.т.д.
Если в критической точке 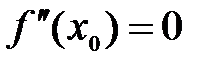 , то в этой точке может быть или максимум, или минимум или не быть ни максимума, ни минимума. В этом случае исследование проводится с помощью первой производной.
, то в этой точке может быть или максимум, или минимум или не быть ни максимума, ни минимума. В этом случае исследование проводится с помощью первой производной.
Пример: Исследовать на максимум и минимум функцию.
а) 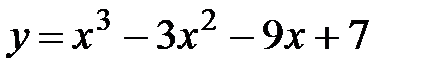 .
.
1. Область определения функции D(y)=R.
2. 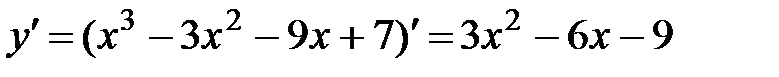 .
.
Критические точки: 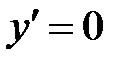 .
. 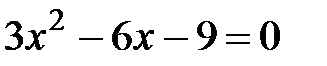 ,
, 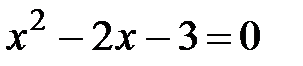 Þ
Þ 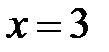 ,
, 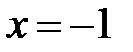 .
.
3. 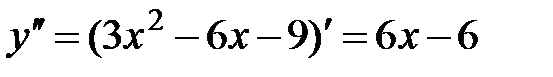 .
.
| x | x=-1 | x=3 |
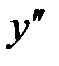
| -12 | 12 |
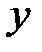
| max y(-1)=12 | min y(3)=-20 |
б) 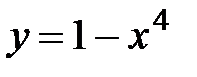 .
.
1. Область определения функции D(y)=R.
2. 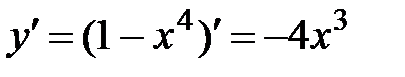 .
.
Критические точки: 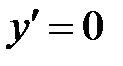 .
. 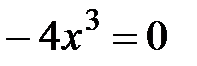 Þ
Þ 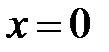 .
.
3. 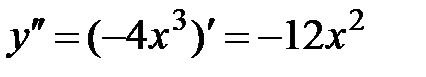 .
.
| x | (-∞;0) | x=0 | (0;+∞) |
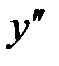
| 0 | ||
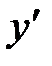
| + | 0 | – |
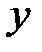
| возрастает | max y(0)=1 | возрастает |
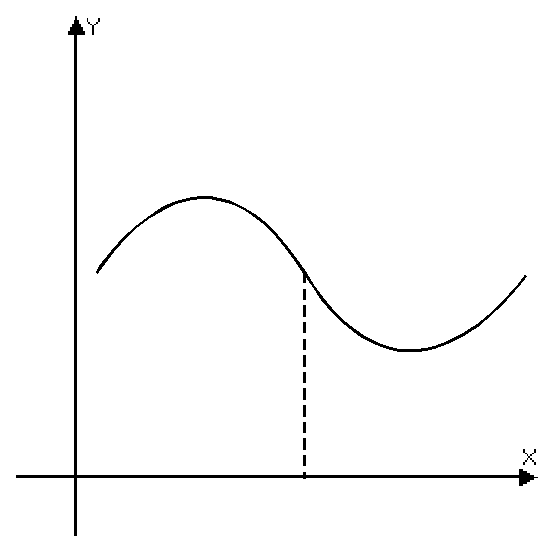
Выпуклые и вогнутые функции.
Пусть функция 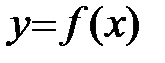 дифференцируема на интервале (a;b). Тогда на этом интервале в каждой точке графика функции существует касательная, причем не параллельная оси OY.
дифференцируема на интервале (a;b). Тогда на этом интервале в каждой точке графика функции существует касательная, причем не параллельная оси OY.
Определение: Функция называется выпуклой, если ее график лежит над любой касательной, проведенной к этому графику.
Определение: Функция называется вогнутой, если ее график лежит под любой касательной, проведенной к этому графику.
На разных участках промежутка функция может быть выпуклой или вогнутой.
Признак выпуклости.
Пусть функция 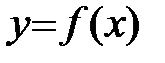 имеет на интервале (a;b) непрерывную производную второго порядка. Если
имеет на интервале (a;b) непрерывную производную второго порядка. Если 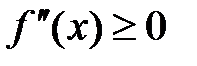 , то функция выпукла на промежутке (a;b). Если
, то функция выпукла на промежутке (a;b). Если 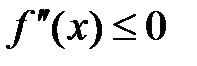 , то функция вогнута на промежутке (a;b).
, то функция вогнута на промежутке (a;b).
Доказательство:
Пусть для определенности на (a;b) 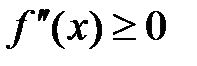 .
.
Возьмем точку x0Î(a;b) и составим уравнение касательной к графику функции в точке с абсциссой x0:
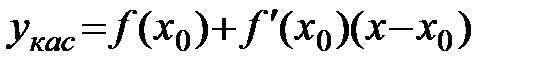 (1)
(1)
Разложим функцию 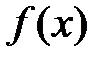 в окрестности точки x0 по формуле Тейлора, причем возьмем два члена разложения и остаточный член:
в окрестности точки x0 по формуле Тейлора, причем возьмем два члена разложения и остаточный член:
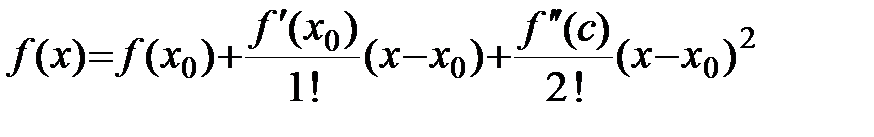 ,
, 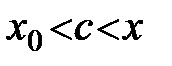 (2)
(2)
| x |
| y |
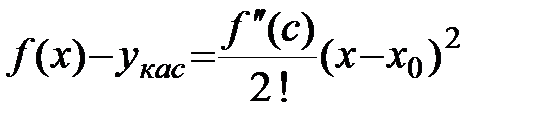 .
.
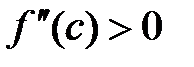 на (a;b)
на (a;b) 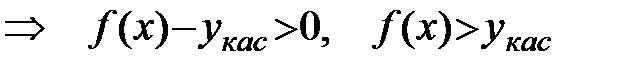 .
.
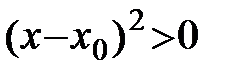
График функции проходит над касательной.
Тогда по определению: функция выпукла.
Вогнутость доказывается аналогично.
Ч.т.д.
Замечание: Условие 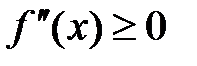 (
(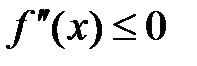 ) является не только достаточным, но и необходимым для выпуклых (вогнутых) функций.
) является не только достаточным, но и необходимым для выпуклых (вогнутых) функций.
Определение: Точка, отделяющая промежуток выпуклости функции от промежутка ее вогнутости, называется точкой перегиба.
Необходимые условия существования точки перегиба функции.
Пусть функция 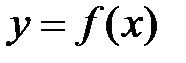 в точке x0 имеет точку перегиба. Если в этой точке существует производная второго порядка, то она обращается в ноль
в точке x0 имеет точку перегиба. Если в этой точке существует производная второго порядка, то она обращается в ноль 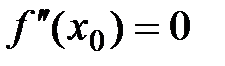 или не существует.
или не существует.
Точки перегиба следует искать среди точек, вторая производная которых равна нулю (y²=0) или не существует. Такие точки называются критическими точками второго рода.
Достаточное условие точки перегиба функции.
Пусть 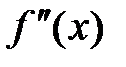 непрерывна в окрестности точки
непрерывна в окрестности точки 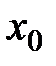 , за исключением, может быть, самой точки
, за исключением, может быть, самой точки 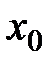 . Если «при переходе» через
. Если «при переходе» через 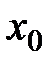
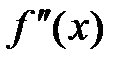 меняет знак, то точка
меняет знак, то точка 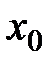 — точка перегиба.
— точка перегиба.
Доказательство:
Пусть «при переходе» через точку 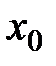
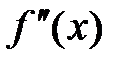 меняет знак с «+» на «-».
меняет знак с «+» на «-».
| + |
| - |
| x0 |
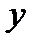
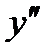
Тогда слева от точки 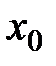 — функция выпукла, а справа — вогнута. Тогда по определению: точка
— функция выпукла, а справа — вогнута. Тогда по определению: точка 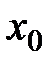 — точка перегиба.
— точка перегиба.
Ч.т.д.
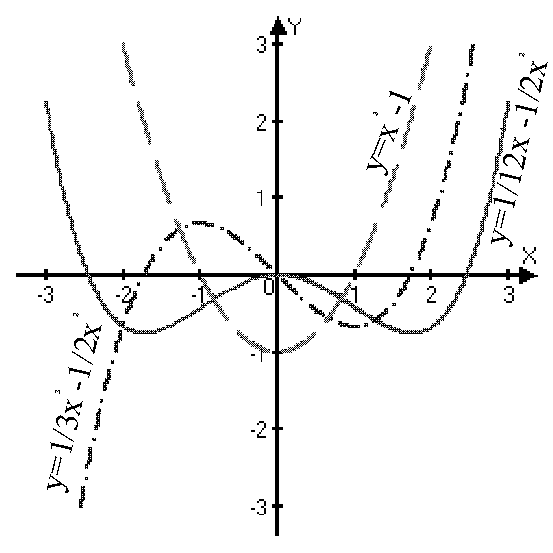 Пример: Исследовать функцию на перегиб.
Пример: Исследовать функцию на перегиб. 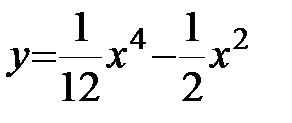 .
.
D(y)=R.
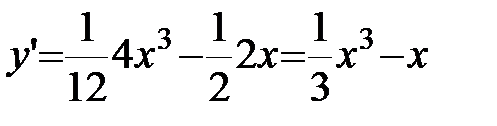 ;
; 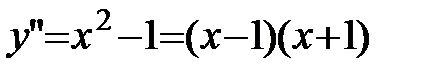 .
.
Критические точки второго рода:
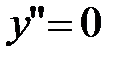 :
: 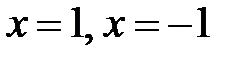 ;
;
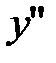 не существует: точек нет.
не существует: точек нет.
При переходе через точки 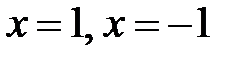 вторая производная
вторая производная 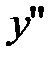 меняет знак.
меняет знак.
Þ 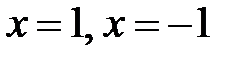 — точки перегиба.
— точки перегиба.
Асимптоты графика функции.
Определение: Прямая l называется асимптотой графика функции 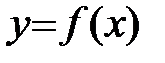 , если расстояние от точки М на графике до прямой l стремится к нулю при удалении точки М по графику функции от начала координат.
, если расстояние от точки М на графике до прямой l стремится к нулю при удалении точки М по графику функции от начала координат.
Асимптоты бывают вертикальные, горизонтальные, наклонные.
Вертикальной асимптотой называется прямая x=a, если 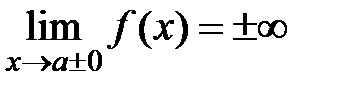 .
.
Находят вертикальную асимптоту по точкам разрыва второго рода (бесконечный разрыв).
Наклонной асимптотой называется асимптота, уравнение которой имеет вид: 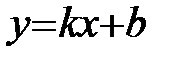 .
.
Оказывается, что если 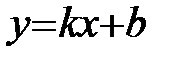 является асимптотой, то
является асимптотой, то 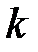 и
и 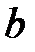 в уравнении определяются следующим образом
в уравнении определяются следующим образом 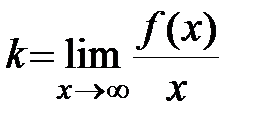 ,
, 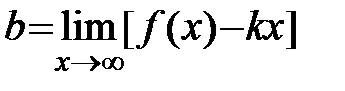 .
.
Доказательство:
| y |
| x |
| f(x) |
| kx+b |
| x |
| N |
| Q |
| M(x;y) |
| y=kx+b |
| асимптота |
| график функции |
По определению асимптоты: если ОМ 
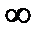 , то |MN|
, то |MN| 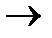 0.
0.
Þ |MQ|→0 при x→±∞, т.к. 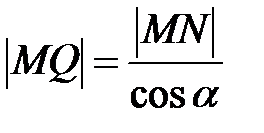 .
.
По чертежу: 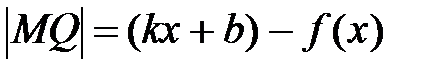 .
.
Перейдем к пределу при x→±∞:
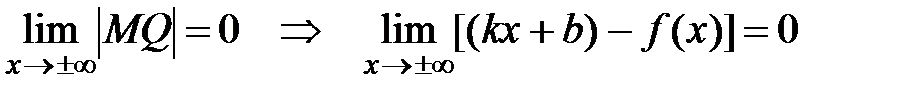 (*)
(*)
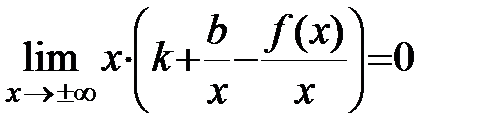
Þ 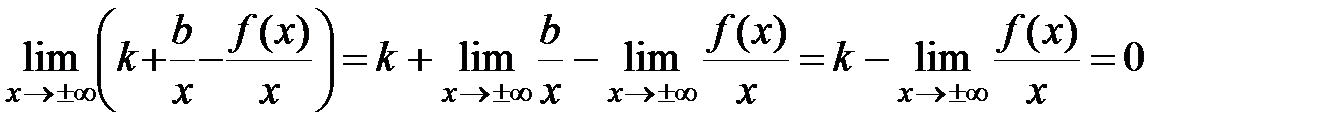 .
.
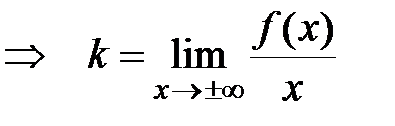 .
.
Из (*) Þ 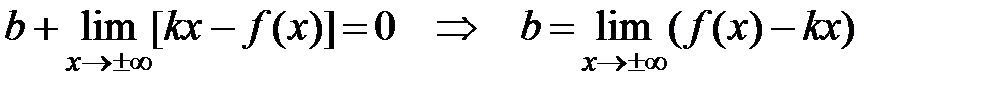 .
.
Ч.т.д.
Замечание 1: Чтобы у кривой были наклонные асимптоты, нужно, чтобы соответствующие пределы в определении k и b были конечными, причем предел при x→+∞ и предел при x→-∞ нужно вычислять отдельно.
Замечание 2: Если k=0, то y=b. Наклонная асимптота в этом случае называется горизонтальной.
Замечание 3: Кривая никогда не пересекает вертикальную асимптоту, а горизонтальные и наклонные асимптоты кривая может пересекать и даже бесконечное число раз.
Пример: Найти асимптоты графика функции 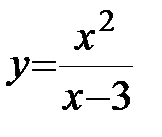 .
.
D(y): x¹3.
Þ x=3 – точка разрыва.
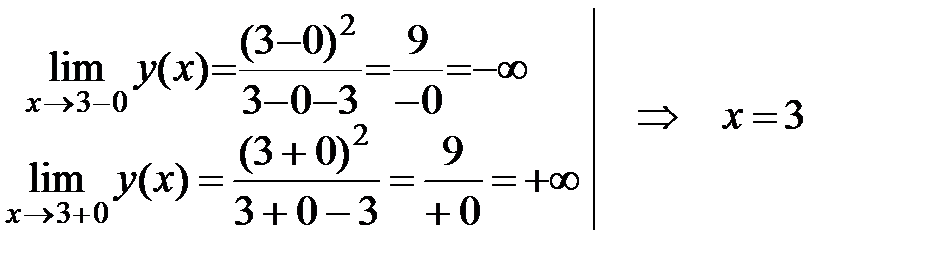 — вертикальная асимптота.
— вертикальная асимптота.
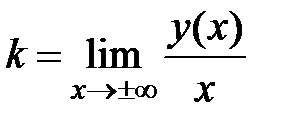 =
= 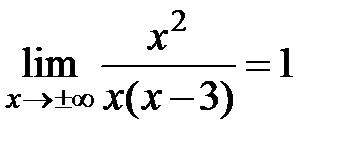 ;
;
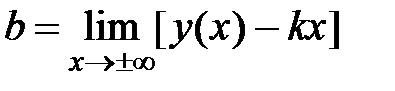 =
= 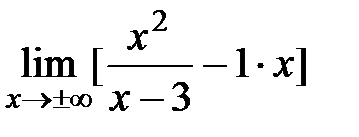 = =
= = 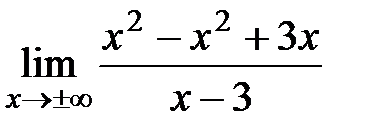 =3 Þ
=3 Þ 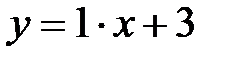 .
.
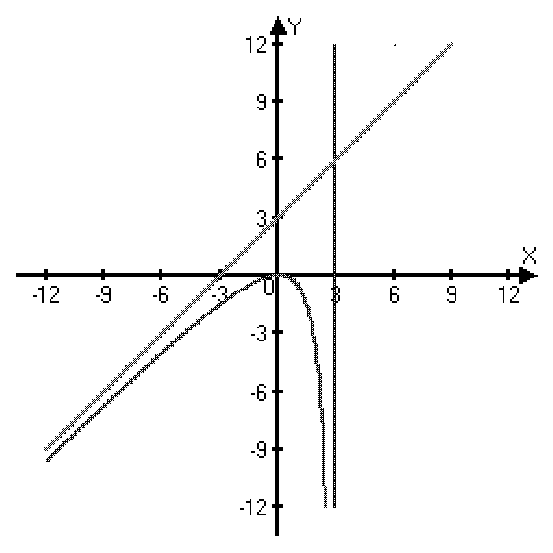
Þ
 2020-05-11
2020-05-11 503
503






