ПРАКТИЧЕСКАЯ РАБОТА
ПЛОЩАДЬ ПОВЕРХНОСТИ СФЕРЫ И ОБЪЕМ ШАРА.
Цель: закрепить навыки решения практических задач на вычисление площади поверхности сферы и объема шара
Теоретическая часть:
СФЕРА.
Определение: Сферой называется поверхность, состоящая из всех точек пространства, которые расположены на данном расстоянии от данной точки.
Основные элементы:
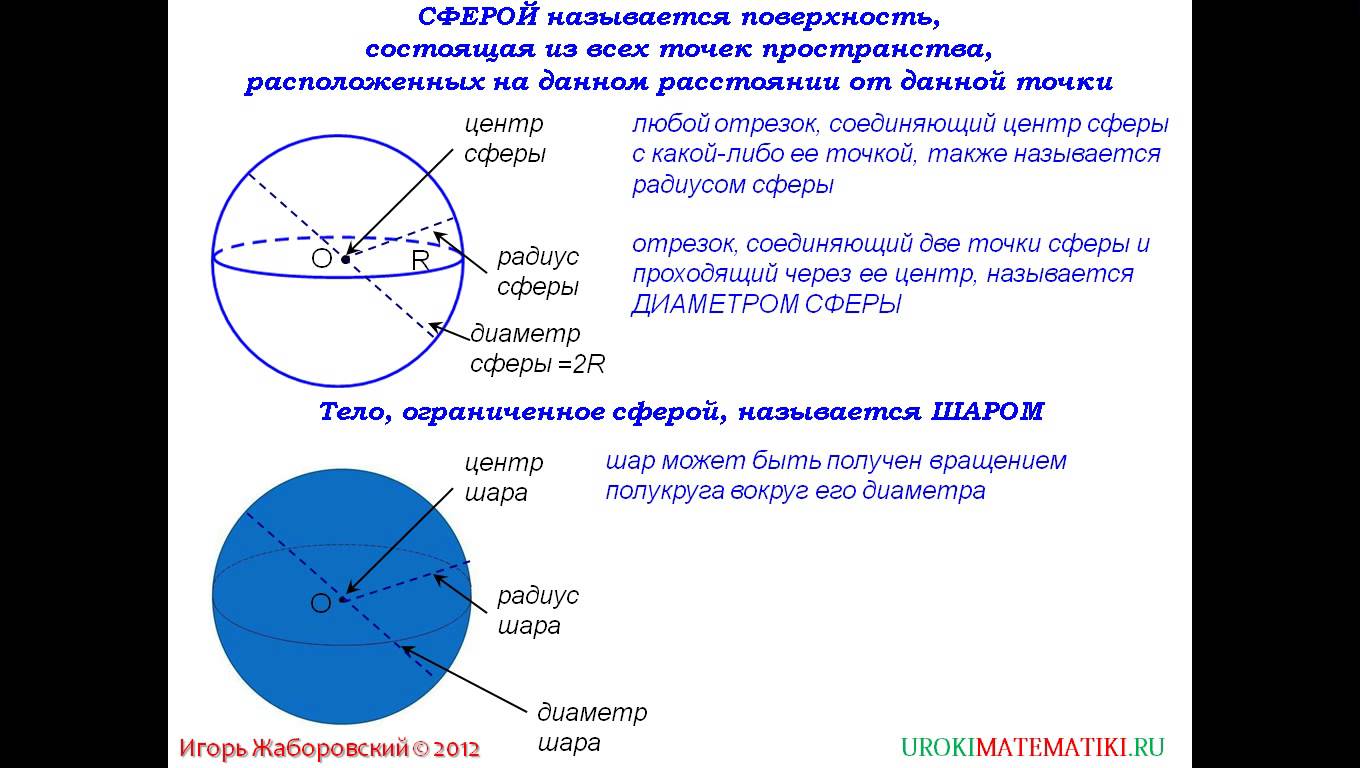
Рис. 1.
Данная точка – центр сферы.
Данное расстояние – радиус сферы.
Радиус сферы – любой отрезок, соединяющий центр и какую-нибудь точку сферы.
Диаметр сферы – отрезок, соединяющий две точки сферы и проходящий через ее центр. Диаметр сферы равен 2R.
Сфера может быть получена вращением полуокружности вокруг ее диаметра.
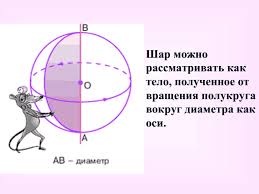
Рис. 2.
Площадь сферы:
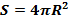 ,
,
где 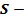 площадь сферы;
площадь сферы;
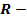 радиус сферы;
радиус сферы;
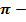 постоянная, равная 3, 14.
постоянная, равная 3, 14.
ШАР.
Определение: Шаром называется тело, ограниченное сферой.
Основные элементы:
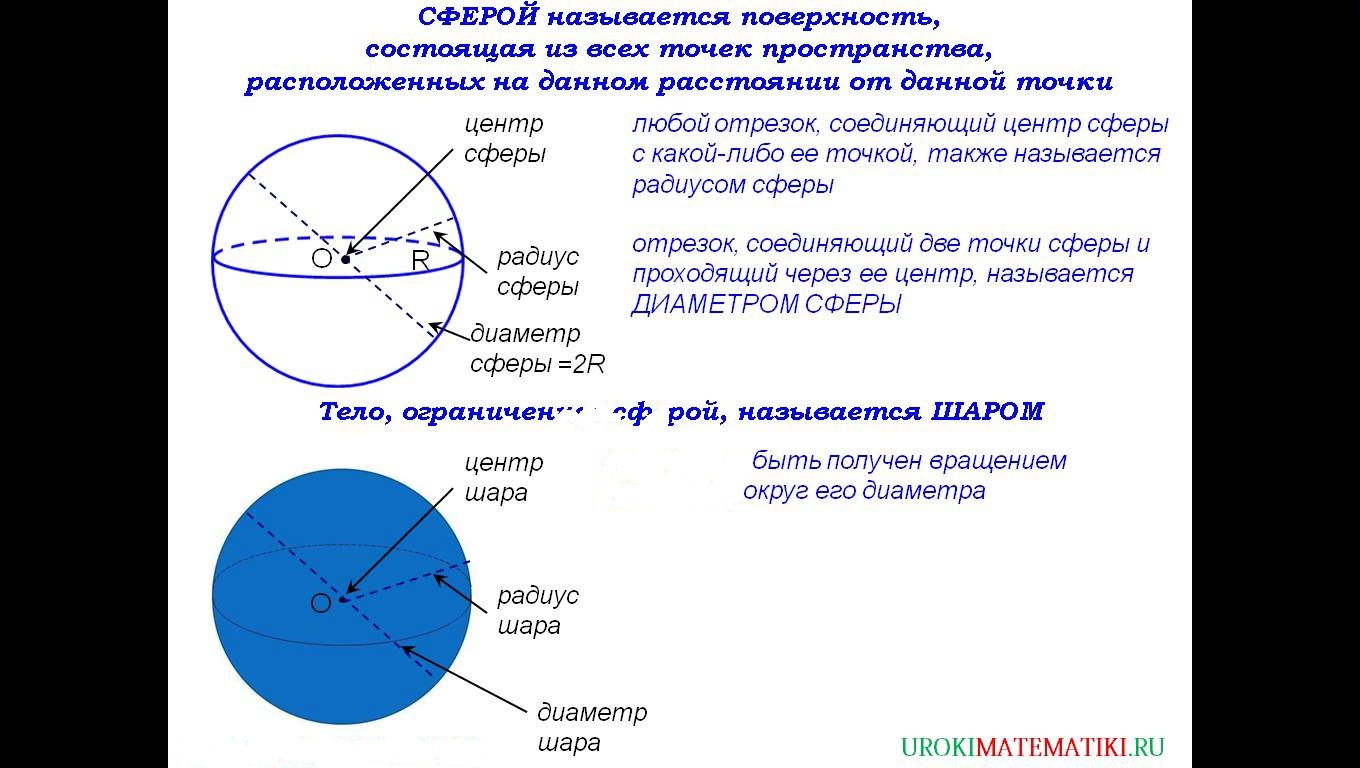
Рис. 4.
Радиус шара – любой отрезок, соединяющий центр и какую-нибудь точку сферы.
Диаметр шара – отрезок, соединяющий две точки сферы и проходящий через ее центр. Диаметр сферы равен 2R.
Центр шара – точка О.
Теорема: Объем шара радиуса R равен
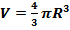 ,
,
где 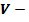 объём шара;
объём шара;
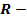 радиус шара;
радиус шара;
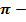 постоянная, равная 3, 14.
постоянная, равная 3, 14.
| Части шара | ||||
Шаровый сегмент
часть шара отсекаемая от него какой-нибудь плоскостью | Шаровый сектор
тело, полученное вращением кругового сектора с углом, меньшим | Шаровый слой часть шара, заключенная между двумя параллельными секущими плоскостями | ||
|
| ||||
Объем шарового сегмента: 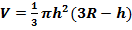 , где V , где V  объем шарового сегмента; объем шарового сегмента; 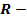 радиус шара; радиус шара; 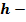 высота сегмента высота сегмента 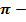 постоянная, равная 3, 14. постоянная, равная 3, 14. | Объем шарового сектора:
где V
| Объем шарового слоя:
где
| ||
Площадь сегментовой поверхности: 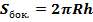 , где , где  площадь сегментовой поверхности шара; площадь сегментовой поверхности шара; 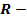 радиус шара; радиус шара; 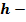 высота сегмента высота сегмента 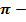 постоянная, равная 3, 14. постоянная, равная 3, 14. | Площадь полной поверхности:
где
| Площадь боковой поверхности:
где
| ||
Упражнения:
1. Найдите площадь сферы, если радиус сферы равен:
а) 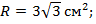
б) 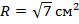
2. Площадь сферы равна 256π см2. Найдите радиус сферы.
3. Найдите объем шара, если радиус R равен 0,75 см.
4. Найдите радиус шара, если объем шара равен 576π м3
1. Найдите площадь сферы, если радиус равен:
а) 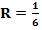 дм;
дм;
б) 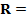 5 см;
5 см;
в) 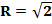 м;
м;
г) 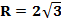 см
см
| Дано: | Решение: |
а) 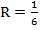 дм; б) дм; б) 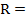 5 см; в) 5 см; в) 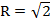 м; г) м; г) 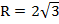 см см 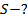 | Площадь сферы равна: 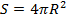 . Подставляем а) . Подставляем а) 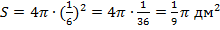 б) б) 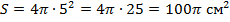 в) в) 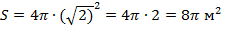 г) г) 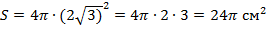 |
| Ответ: а) б) в) г) | |
2. Площадь сферы равна 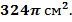 Найдите радиус R сферы.
Найдите радиус R сферы.
| Дано: | Решение: |
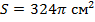 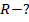 | Формула площади сферы: 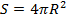 . . 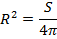 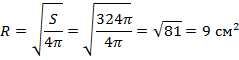 |
| Ответ: | |
3. Найдите объем шара, если радиус R равен 3 см.
| Дано: | Решение: |
| R = 3 см V -? | Формула объёма шара: 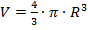 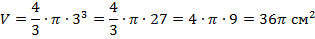 |
| Ответ: | |
4. Найдите радиус шара, если объем шара равен 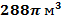
| Дано: | Решение: |
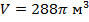 R -? R -? | Формула объёма шара: 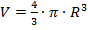 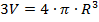 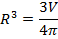 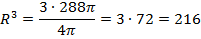 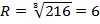 м м |
| Ответ: | |
Часть А:
1. Напишите название элементов сферы
2. Объем шара равен 288π см3. Найдите диаметр шара.
Часть В:
Вставьте пропущенное слово.
1. Поверхность, состоящая из всех точек пространства, которые расположены на данном расстоянии от данной точки, называется _____________.
2. ___________ – любой отрезок, соединяющий центр и какую-нибудь точку сферы.
3. ___________ – отрезок, соединяющий две точки сферы и проходящий через ее центр.
4. Сфера может быть получена вращением __________ вокруг ее диаметра.
5. Запишите формулу нахождения площади сферы.
Часть С:
Решить задачу.
1. Объём шара равен 12348π см3. Найдите площадь его поверхности, деленную на π.
 2020-05-12
2020-05-12 766
766
 , вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов
, вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов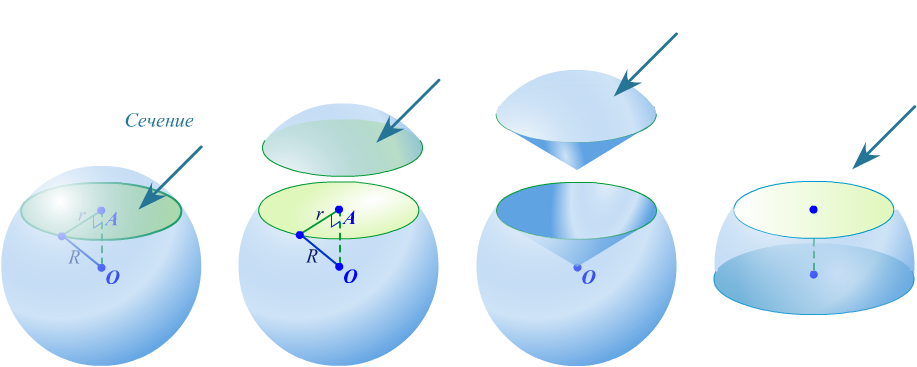
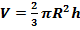 ,
,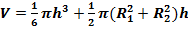 ,
,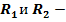 радиусы оснований слоя;
радиусы оснований слоя;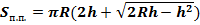 ,
,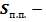 площадь полной поверхности шарового сектора;
площадь полной поверхности шарового сектора;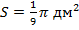
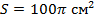
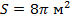
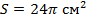
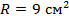
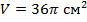
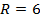 м
м






