Проведение линейной и сплайновой аппроксимации

Одномерная линейная аппроксимация. Для представления физических закономерностей и при проведении научно-технических расчетов часто используются зависимости вида y (x), причем число точек этих зависимостей ограничено. Возникает задача приближенного вычисления значений функции в промежутках между узловыми точками (интерполяция) и за их пределами (экстраполяция). Эта задача решается аппроксимацией исходной зависимости, т.е. ее подменой какой-либо достаточно простой функцией. Система MathCAD предоставляет возможность аппроксимации двумя важными типами функций: кусочно-линейной и сплайновой.

& При кусочно-линейной интерполяции вычисления дополнительных точек выполняются по линейной зависимости. Графически это означает просто соединение узловых точек отрезками прямых, для этого используется функция linterp (VX,VY, x).

& Для заданных векторов VX и VY узловых точек и заданного аргумента x linterp (VX,VY, x) возвращает значение функции при ее линейной аппроксимации. При экстраполяции используются отрезки прямых, проведенных через две крайние точки.

Задача_5. Рассмотрим использование этой функции на примере. Пусть задаются 10 точек: по оси Ox – целые числа, их значение по оси Oy есть случайная величина.

¿ _5. 1) Зададим начальные значения и массив экспериментальных данных (X,Y), исходный массив данных Y задается генератором случайных чисел rnd:

2) Вычислим интерполирующее значение в одной точке X=5:

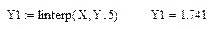
3) Самостоятельно вычислить интерполирующее выражение в точке 6,23.

4) Построить график зависимости Y от X. Выбрать тип линии – точки (points), толщиной – 3.

5) Зададим теперь массив Ym интерполирующих значений массива Yв m точках. Задать перед графиком:

6) Построить на имеющемся графике еще одну зависимость –Ym от Xm. Выбрать тип линии – точки (points), толщиной – 3, изменив символы точек. Просмотреть и проанализировать результат.

7) Наконец, перед графиком зададим непрерывную интерполирующую функцию, которую назовем Ylin, которая пройдет через все точки от 0 до max(X):

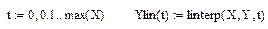
8) Построить на имеющемся графике зависимость Ylin от t.

 

& При небольшом числе узловых точек гораздо лучшие результаты дает сплайн-аппроксимация. При ней исходная функция заменяется отрезками кубических полиномов, проходящих через три смежные узловые точки. Коэффициенты полиномов рассчитываются так, чтобы непрерывными были первая и вторая производные. Линия, которую описывает сплайн-функция напоминает по форме гибкую линейку, закрепленную в узловых точках.

Для осуществления сплайновой аппроксимации система MathCAD предлагает функции:

interp (VS,VX,VY,x) – возвращает значение y(x) для заданных векторов VS, VX, VY и заданного значения x, при этом

VS – вектор вторых производных, созданный функцией cspline(X,Y), pspline(X,Y) или lspline(X,Y);

VX – вектор опытных значений аргумента, расположенных в порядке возрастания;

VY – вектор опытных значений функции;

x – значение аргумента, при котором вычисляется интерполирующее значение функции.

& Для определения вектора VS используется одна из следующих функций:

cspline (VX,VY) – возвращает VS вектор коэффициентов кривой, которая приближается к кубической параболе в граничных точках;

pspline (VX,VY) – возвращает VS вектор коэффициентов кривой, которая приближается к квадратичной параболе в граничных точках;

lspline (VX,VY) – возвращает VS вектор коэффициентов кривой, которая приближается к прямой линии в граничных точках;

Сплайн-аппроксимация проводится в два этапа:

1) С помощью функции cspline, pspline или lspline отыскивается вектор VS вторых производных функции y(x), заданной векторами VX, VY ее значений (абсцисс и ординат).

2) Для каждой искомой точки вычисляется значение y(x) с помощью функции interp.

Задача_6. Применим описанные функции к рассмотренному выше примеру и сравним получающиеся результаты.

¿ _6. 1) Задать

2) Задать аппроксимирующие функции, используя каждый их этих векторов. Назовем функции Ylsp(t), Ypsp(t), Ycsp(t), где t, как и выше, ранжированная переменная:

3) Для сравнения результатов, построить график зависимости Y от X (отобразить точки). На этом же графике построить зависимости Ylin, Ylsp, Ypsp, Ycsp от t. 

Задача_7.    Пусть задается вектор исходных данных

Задать линейно-интерполирующую функцию и сплайн-итерполирующую функцию. Построить графики и сравнить результаты.

  & Функция csort (M,n) переставляет строки матрицы таким образом, чтобы отсортированным оказался n-ый столбец.

¿ _7. 1) Так как вектор X – это нулевой столбец матрицы V, упорядочим его функцией csort (V,0).

2) Присвоим векторам X и Y значения из нулевого и из первого столбца матрицы соответственно:

 

3) Задать интерполирующую (линейно) функцию lint(x) и вычислить ее значения в точках 2 и 7,71.

4) Сплайн-интерполяция: зададим вектор SV, используя cspline(X,Y).

5) Задать интерполирующую функцию fits(x) и вычислим fits(2) и fits(7,71).

6) Определим индексы i и j: i изменяется от 0 до длины вектора X минус 1;

7) Введем переменную q равную 100; зададим j в диапазоне от 0 до q. Вычислим .

8) Представим графически данные массива и линейно-интерполирующую функцию и данные массива и сплайн-интерполирующую функцию. Построить в одном шаблоне графики функций Y(X) и lint(x_j); в другом шаблоне Y(X) и fits(x_j). Для первого графика задать точечный тип линии.