Формула Ньютона-Лейбница

Теорема. Если функция 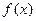непрерывна на отрезке 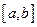, а F(x) – любая ее первообразная, то имеет место формула

                 ,

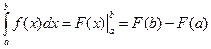 которая называется формулой Ньютона-Лейбница.

 

Вычислить интегралы:

 

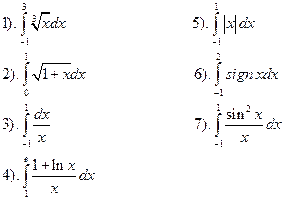
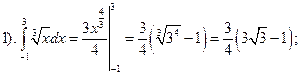
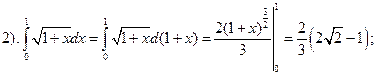
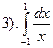 не существует, так как  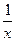не ограничена.

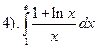, подынтегральная функция непрерывна на 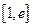, следовательно, можно применить формулу Ньютона-Лейбница

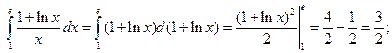
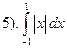. Первообразную от  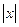мы не знаем. Можно воспользоваться свойством аддитивности интеграла

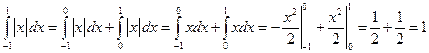
Существует также свойство интеграла на симметричном промежутке

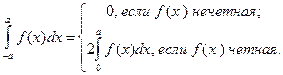
Так как 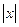 - четная функция, то .

 

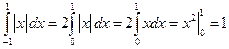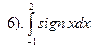. Нельзя применить формулу, так как функция разрывная. Применим свойство аддитивности 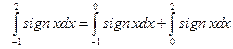. На промежутке 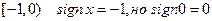. Воспользуемся теоремой: если изменить значение интегрируемой функции в одной точке (или в конечном числе точек), то значение интеграла не изменится, так как 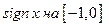имеет одну точку разрыва и ограничена, следовательно, она интегрируема. Тогда изменим значение  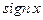в точке  и положим в первом интеграле подынтегральную функцию 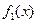, а во втором аналогично 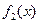, тогда

                        .

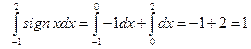Здесь воспользовались формулой .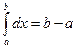

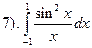. Функция интегрируема, так как точка разрыва одна () функция ограничена на промежутке 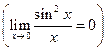. Первообразная не выражается в элементарных функциях и формулу Ньютона-Лейбница нельзя применить. Но функция четная, а промежуток симметричный, значит, интеграл равен нулю.

 

 

Интегрирование по частям.

Если функци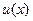и и 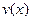 интегрируемы вместе со своими производными на отрезке 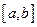, то имеет место формула интегрирования по частям

                                         .

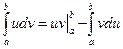Формула остается справедливой, если вместо непрерывности производных потребовать только их интегрируемость.

 

Вычислить интегралы:

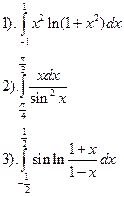
1). Функция четная, промежуток симметричный.

        

 

.

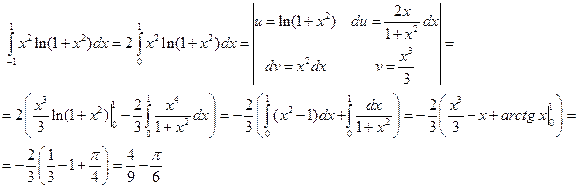
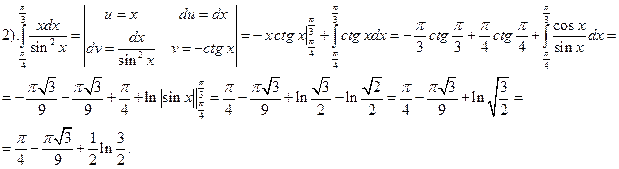
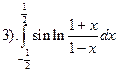 Проверим, что подынтегральная функция является нечетной

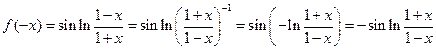
Так как на этом промежутке функция непрерывна, следовательно, она интегрируема и промежуток симметричный, а, значит, интеграл равен нулю.

 

Формула замены переменного.

Пусть функция 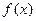непрерывна на отрезке 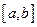, функция  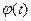определена и непрерывна вместе со своей производной 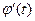на отрезке 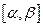, причем для всех  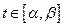выполняется неравенство  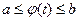и, следовательно, имеет смысл сложная функция 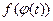. Если при этом 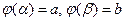, то имеет место формула

                                    ,

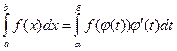 которая называется формулой замены переменной в определенном интеграле.

Вычислить интегралы:

.

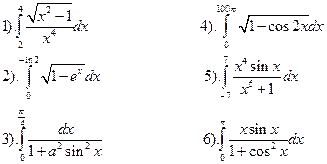
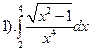Сделаем замену 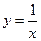 , тогда .

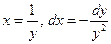Найдем новые пределы   

                                              

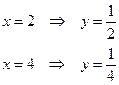
Так как 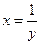 - непрерывно дифференцируема на 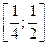, то применим формулу замены переменной

,

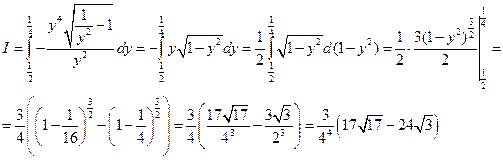Здесь 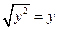, так как .

 

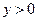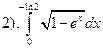. Сделаем замену:

     

 

 

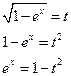
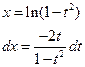
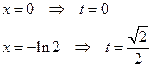
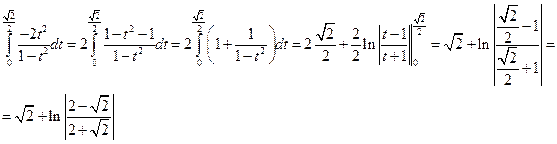
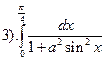. Интеграл вида 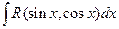, причем 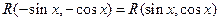, значит, применим подстановку  .

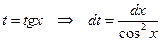Преобразуем интеграл к удобному виду

               

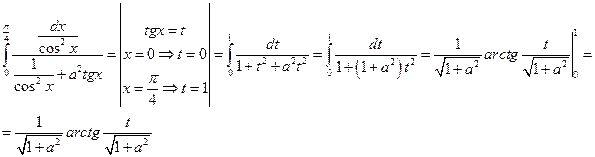
Замена в определенном интеграле удобна тем, что не надо возвращаться к старой переменной, достаточно поменять пределы.

 

 

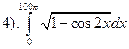
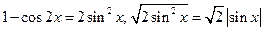
С помощью формулы замены переменной легко доказать теорему:

Если 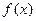 - непрерывная на всей числовой прямой периодическая с периодом T функция, то для любого числа 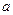выполняется равенство

                                .

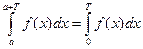Наша функция имеет период 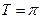, тогда

.

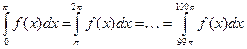Тогда .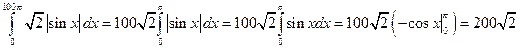

 

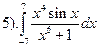. Функция нечетная, промежуток симметричный, интеграл равен нулю.

 

.

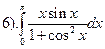Можно проверить, что 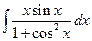 не берется, но с помощью замены переменной можно убрать не берущуюся часть

                                 

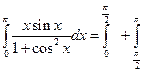
Во втором интеграле сделаем такую замену, чтобы пределы интегрирования совпали с первым интегралом. Это будет при .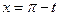

Тогда при .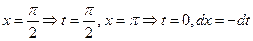

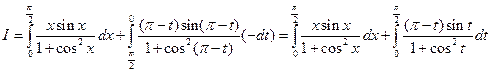
Если второй интеграл разбить на разность двух и вместо t подставить x, то не берущаяся часть пропадет и останется только

.

 

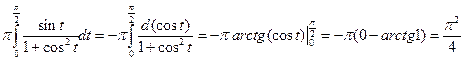7). Можно ли в интеграле 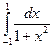 сделать замену  ?

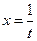По теории функция 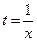 должна быть непрерывна вместе со своей производной на промежутке 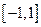, но это не выполняется. Поэтому замену сделать нельзя. Посмотрим все же, что получится при такой замене.

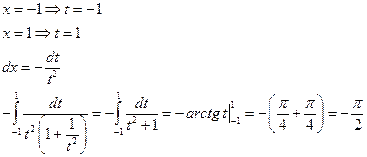
Интеграл получился отрицательный, хотя подынтегральная функция была строго больше нуля. При неверном применении формулы вышел неверный ответ.

 

8). Найти ошибку при следующей замене переменной.

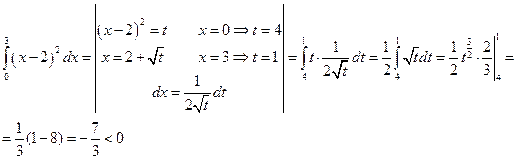
Ответ не верен, так как под интегралом стояла положительная функция. Ошибка в том, что 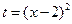 переводит отрезок  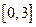в отрезок 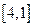, однако обратной функции здесь не существует 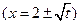, а найденная обратная функция при  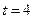не дает . Лучше при подстановке брать функцию монотонную, тогда не будет проблем с обратной функцией.