Основные теоретические сведения

Пирамида.

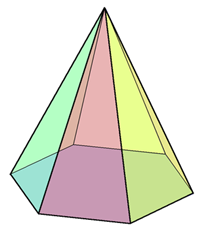Элементы пирамид

боковые грани — треугольники, сходящиеся в вершине;

боковые ребра — общие стороны боковых граней;

вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания;

высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания

диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания;

основание — многоугольник, которому не принадлежит вершина пирамиды.

 

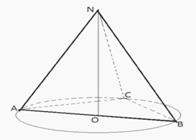В основании пирамиды лежит прямоугольный треугольник.

NO - высота пирамиды.

O - середина гипотенузы АВ.

O – центр описанной окружности.

OC = OA = OB.

 

Если все боковые рёбра равны, то:

· вокруг основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр;

· боковые рёбра образуют с плоскостью основания равные углы;

Если боковые грани наклонены к плоскости основания под одним углом, то:

· в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр;

· высоты боковых граней равны;

· площадь боковой поверхности равна половине произведения периметра основания на высоту боковой грани.

Пирамида называется правильной, если в основании лежит правильный многоугольник, а ее высота падает в центр основания.

Апофема — высота боковой грани правильной пирамиды, проведённая из её вершины.

Свойства правильной пирамиды:

· боковые рёбра правильной пирамиды равны;

· в правильной пирамиде все боковые грани — равные равнобедренные треугольники;

· в любую правильную пирамиду можно как вписать, так и описать вокруг неё сферу;

· если центры вписанной и описанной сферы совпадают, то сумма плоских углов при вершине пирамиды равна 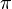, а каждый из них соответственно 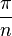, где n — количество сторон многоугольника основания;

 

 

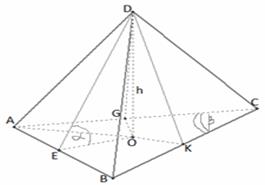 DO - высота пирамиды.

DAO - угол между боковым ребром и плоскостью основания.

DKO - угол между боковой гранью и плоскостью основания.

DK – апофема.

 

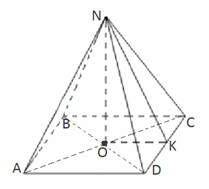
NO - высота пирамиды,

NDO - угол между боковым ребром и плоскостью основания

NKO - угол между боковой гранью и плоскостью основания

NK - апофема.

Формулы

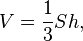 где 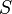— площадь основания и 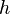— высота;

 

Объём треугольной пирамиды может быть вычислен по формуле:

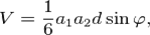где 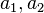— скрещивающиеся рёбра, 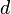— расстояние между 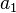и 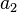, 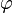— угол между 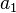и ;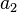

· Боковая поверхность — это сумма площадей боковых граней:

· Полная поверхность — это сумма площади боковой поверхности и площади основания:

· Площадь боковой поверхности в правильной пирами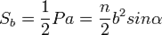де:

где 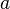— апофема, 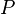— периметр основания, 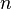— число сторон основания, 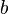— боковое ребро, 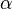— плоский угол при вершине пирамиды.

Тетраэдр.