Операция отыскания производной называется дифференцированием

Занятие №85

Тема: Связь между дифференцируемостью и непрерывностью функций. Формулы дифференцирования.

Операция отыскания производной называется дифференцированием.

Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного - в правилах дифференцирования.

Пример 1. Найти производную функции

.

Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.

.

Из таблицы производных выясняем, что производная "икса" равна единице, а производная синуса - косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:

.

Пример 2. Найти производную функции

.

Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:

Пример 3. Найти производную функции

.

.

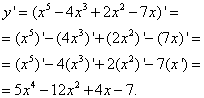Пример 4. Найти производную функции

.

Решение. Допустим, с производной косинуса всё понятно, скажут многие, начинающие изучать производные. А как быть с производной синуса двенадцати, делённых на пи? Ответ: считать равной нулю! Здесь синус (функция всё-таки!) - ловушка, потому что аргумент - не переменная икс или любая другая переменная, а просто число. То есть, синус этого числа - тоже число. А производная числа (константы), как мы знаем из таблицы производных, равна нулю. Итак, оставляем только минус синус икса и находим его производную, не забывая про знак:

.

Ответ:

.

Пример 5. Найти производную функции

.

Решение. Второе слагаемое - тот же случай, что и первое слагаемое в предыдущем примере. То есть, число, а производная числа равна нулю. Находим производную второго слагаемого как производную частного:

Ответ:

Пример 6. Найти производную функции

.

Решение. Находим производную первого слагаемого:

.

Находим производную второго слагаемого:

.

Находим производную третьего слагаемого:

.

Здесь двойка перед иксом - постоянный множитель, поэтому его просто вынесли за знак производной.

Собираем всё вместе:

.

Если требуется в окончательном решении получить выражение с корнями, то преобразуем степени в корни и получаем искомую производную:

.

Пример 7. Найти производную функции

.

Решение. Находим производную первого слагаемого:

.

Здесь первая двойка в числителе промежуточного выражения была константой, её производная равна нулю.

Находим производную второго слагаемого:

Находим производную третьего слагаемого:

Здесь применяли знания из школьного курса о действиях с дробями, их преобразовании и сокращении.

Собираем всё вместе, обращая внимание на то, что знаки производных первого и третьего слагаемых противоположны знакам слагаемых в исходном выражении:

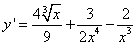.Самостоятельная работа

В тетрадях для лекций записать теорию и решить задачи!

 Только решение самостоятельной работы отправляете по электронной почте:

luda181929@yandex.ru

В работе указывайте ФИО и группу

Пожалуйста, задания отправляйте по расписанию занятий, но не позднее следующего занятия, иначе такие работы не будут проверяться!!!