2020-05-13
230
Основой для вычисления статистической оценки параметра системы является реализация случайной величины, которая формируется во время прогонов вероятностной имитационной модели.
Для оценки математического ожидания случайной величины используется формула
,
где 
– значения случайной величины, которые принадлежат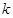 
-му интервалу интервального статистического ряда; 
– частота 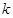-го интервала; 
– общее количество испытаний.
Для оценки дисперсии случайной величины используется формула
Оценка среднего квадратического отклонения:
.
Задание 1. Смоделировать 
экспериментов по схеме Бернулли: эксперимент состоит из 
независимых испытаний, в каждом из которых вероятность появления события 
равна 
.
| № варианта |
|
|
|
| 1 | 8 | 5 | 0,7 |
| 2 | 9 | 6 | 0,6 |
| 3 | 6 | 4 | 0,8 |
| 4 | 7 | 5 | 0,5 |
| 5 | 9 | 7 | 0,65 |
| 6 | 8 | 6 | 0,45 |
| 7 | 6 | 4 | 0,9 |
| 8 | 8 | 6 | 0,55 |
| 9 | 7 | 5 | 0,8 |
| 10 | 9 | 7 | 0,75 |
Задание 2. Смоделировать экспериментов, в каждом из которых происходит одно из событий 
, которые образуют полную группу: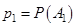 
, 
, 
, 
.
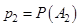| № варианта |
| 
| 
| 
| 
|
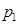
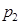
| 1 | 8 | 0,26 | 0,19 | 0,35 | 0,20 |
| 2 | 9 | 0,19 | 0,25 | 0,36 | 0,20 |
| 3 | 6 | 0,20 | 0,24 | 0,31 | 0,25 |
| 4 | 7 | 0,18 | 0,26 | 0,32 | 0,24 |
| 5 | 9 | 0,19 | 0,25 | 0,32 | 0,24 |
| 6 | 8 | 0,17 | 0,27 | 0,32 | 0,24 |
| 7 | 6 | 0,26 | 0,21 | 0,30 | 0,23 |
| 8 | 8 | 0,23 | 0,21 | 0,36 | 0,20 |
| 9 | 7 | 0,24 | 0,21 | 0,32 | 0,23 |
| 10 | 9 | 0,14 | 0,31 | 0,32 | 0,23 |
Задание 3. Смоделировать 4 возможных значения НСВ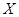 
, равномерно распределенной на отрезке 
.
| № варианта |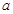 
| 
|
| 1 | 1 | 8 |
| 2 | –2 | 6 |
| 3 | –3 | 9 |
| 4 | 2 | 7 |
| 5 | 4 | 10 |
| 6 | –1 | 7 |
| 7 | 5 | 13 |
| 8 | 2 | 8 |
| 9 | –3 | 5 |
| 10 | –4 | 6 |
Задание 4. Смоделировать 5 возможных значения НСВ 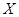, распределенной экспоненциально с параметром 
.
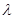| № варианта | 
|
| 1 | 2,0 |
| 2 | 2,5 |
| 3 | 2,0 |
| 4 | 1,5 |
| 5 | 3,5 |
| 6 | 4,5 |
| 7 | 4,0 |
| 8 | 5,0 |
| 9 | 6,5 |
| 10 | 5,5 |
Задание 5. Смоделировать 4 возможных значения НСВ 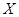, распределенной нормально с параметрам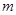и 
и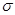 
.
| № варианта |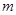
|
|
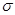
| 1 | 6 | 2 |
| 2 | 4 | 6 |
| 3 | 12 | 4 |
| 4 | 8 | 3 |
| 5 | 20 | 5 |
| 6 | 15 | 7 |
| 7 | 3 | 4 |
| 8 | 10 | 5 |
| 9 | 7 | 3 |
| 10 | 10 | 2 |
Задание 6. Используя результаты 100 имитационных прогонов для оценки времени (в мин.) пребывания посетителей в системе:
1) построить интервальный статистический ряд, разбив область реализаций на 8 одинаковых интервалов;
2) вычислить оценки для математического ожидания, дисперсии, среднего квадратического отклонения;
3) построить гистограмму частот.
| 180+К | 188 | 206 | 190+К | 197 | 167 | 198 | 194 | 210 | 176 |
| 190 | 182 | 160 | 202 | 189-К | 181+К | 200 | 211-К | 188 | 207-К |
| 176 | 186 | 204+К | 170 | 225 | 190 | 180 | 212 | 200-К | 191 |
| 174 | 187 | 184 | 200 | 190 | 222 | 210-К | 192 | 183 | 223-К |
| 197 | 190+К | 178 | 207 | 203 | 174 | 190 | 179+К | 208 | 187 |
| 173 | 193 | 199 | 211-К | 194 | 207 | 179 | 187 | 171+К | 201 |
| 177 | 180 | 188 | 198 | 210+К | 190 | 164 | 182 | 200 | 191 |
| 171-К | 195 | 190 | 166 | 205 | 185 | 217 | 180 | 220 | 191 |
| 192 | 178 | 208-К | 199 | 155 | 191-К | 180+К | 196-К | 172+К | 187+К |
| 194 | 12-К | 211 | 190 | 201 | 182 | 220 | 161 | 188 | 215 |
(К – номер варианта)
ІІІ. Составить отчет. Требования к отчету. В отчете должны быть приведены:1. Краткие теоретические сведения.2. Решение своего варианта с необходимыми пояснениями.
