Практическое занятие № 7-8
Тема: Вероятностное моделирование
Цель работы: Освоить методику моделирования случайных величин и статистической обработки результатов моделирования.
Краткие теоретические сведения.Для имитации случайных явлений различной природы достаточно получить на ЭВМ последовательность значений случайной величины, равномерно распределенной на отрезке 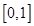 . Процесс принятия значений случайной величиной называют её моделированием.
. Процесс принятия значений случайной величиной называют её моделированием.
Моделирование дискретной случайной величины
Пусть 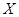 – дискретная случайная величина (ДСВ), которая задана законом распределения
– дискретная случайная величина (ДСВ), которая задана законом распределения
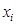
| 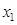
| 
| … | 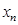
|
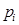
| 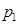
| 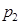
| … | 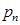
|
Для того чтобы смоделировать дискретную случайную величину 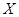 , нужно:
, нужно:
1) Разбить интервал 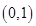 на
на 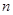 частичных интервалов
частичных интервалов 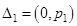 ,
, 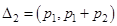 , …,
, …, 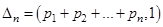 .
.
2) Выбрать случайное число 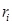 (например, с помощью генератора случайных чисел или из таблицы случайных чисел). Если
(например, с помощью генератора случайных чисел или из таблицы случайных чисел). Если 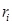 попало в частичный интервал
попало в частичный интервал 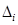 , то считать, что случайная величина
, то считать, что случайная величина 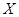 приняла значение
приняла значение 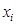 .
.
Моделирование полной группы событий
Пусть 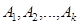 – полная группа событий, наступление которых необходимо исследовать,
– полная группа событий, наступление которых необходимо исследовать, 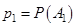 ,
, 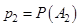 ,…,
,…, 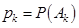 –вероятности наступления этих событий.
–вероятности наступления этих событий.
Для того чтобы смоделировать испытания, в каждом из которых наступает одно из событий 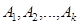 , нужно:
, нужно:
1) смоделировать ДСВ 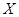 по закону распределения
по закону распределения
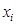
| 1 | 2 | … | 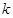
|
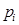
| 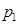
| 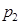
| … | 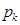
|
2) если в испытании ДСВ 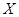 приняла возможное значение
приняла возможное значение 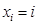 , то считать, что произошло событие
, то считать, что произошло событие 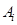 .
.
Моделирование непрерывной случайной величины
Пусть 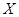 – непрерывная случайная величина (НСВ), которая имеет функцию распределения
– непрерывная случайная величина (НСВ), которая имеет функцию распределения 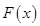 и плотность распределения
и плотность распределения 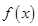 .
.
Для моделирования НСВ 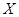 применяют метод обратной функции:
применяют метод обратной функции:
1) Для того, чтобы смоделировать возможное значение 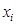 НСВ
НСВ 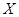 с известной функцией распределения
с известной функцией распределения 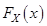 , нужно выбрать случайное число
, нужно выбрать случайное число 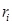 и решить относительно
и решить относительно 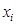 уравнение
уравнение
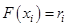 .
.
2) Для того, чтобы смоделировать возможное значение 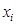 НСВ
НСВ 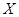 с известной плотностью распределения
с известной плотностью распределения 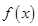 , нужно выбрать случайное число
, нужно выбрать случайное число 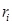 и решить относительно
и решить относительно 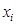 уравнение
уравнение
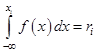
или
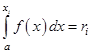
где 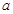 – наименьшее конечное возможное значение НСВ
– наименьшее конечное возможное значение НСВ 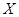 .
.
Для моделирования непрерывной случайной величины, равномерно распределенной на 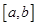 , функцию распределения
, функцию распределения
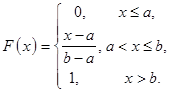
нужно приравнять к случайному числу 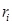 :
:
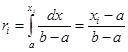
Откуда значение случайной величины, равномерно распределенной на 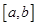 :
:
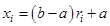 .
.
Для моделирования непрерывной случайной величины, распределенной экспоненциально с параметром 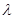 , нужно решить относительно
, нужно решить относительно 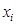 уравнение
уравнение
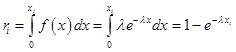 .
.
Откуда значение случайной величины, распределенной экспоненциальнос параметром 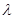 :
:
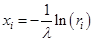 .
.
Для моделирования непрерывной случайной величины, распределенной нормально с параметрами 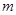 и
и 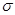 нужно сначала смоделировать непрерывную случайную величину, распределенную стандартно с параметрами
нужно сначала смоделировать непрерывную случайную величину, распределенную стандартно с параметрами 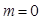 и
и 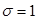 . Для этого вычисляют сумму
. Для этого вычисляют сумму
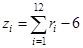
Тогда значения случайной величины, распределенной нормальнос параметрами 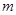 и
и 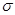 :
:
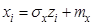 .
.
 2020-05-13
2020-05-13 183
183







