Решите самостоятельно системы уравнений 1-3 (ОГЭ задание 9)

Системы уравнений

Решить систему уравнений – значит найти множество её решений или доказать, что решений нет.

Решением системы двух уравнений с двумя переменными является пара значений переменных, обращающая каждое уравнение системы в верное числовое равенство

Системы уравнений с двумя переменными можно решать:

· способом подстановки;

· способом алгебраического сложения;

· графическим способом

· *способом ведения новых переменных

Способ подстановки «хорош» при решении систем, когда одно из уравнений является уравнением первой степени. Полезно помнить алгоритм решения этим способом:

1.    Из уравнения первой степени выражают одну переменную через другую.

2.    Подставляют полученное выражение в уравнение второй степени

3.    Решают получившееся уравнение.

4.    Находят соответствующие значения второй переменной.

Графический способ применим к решению любой системы, но с помощью графиков уравнений можно приближенно находить решения системы. Лишь некоторые найденные решения системы могут оказаться точными. В этом можно убедиться, подставив их координаты в уравнения системы.

 

1) Решим методом подстановки

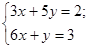
2) Решим методом алгебраического сложения эту же систему

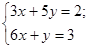
Сделаем выводы о преимуществах и недостатках методов.

Выбор способа решения зависит от уравнений, входящих в систему.

3) Решить систему

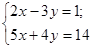
4) Решить систему

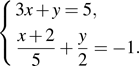
Решение.

Подставим 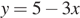во второе уравнение системы, получим уравнение относительно 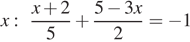. Отсюда . Подставим в уравнение 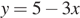, получим: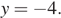

 

Ответ: (3; −4).

 

Решите самостоятельно системы уравнений 1-3 (ОГЭ задание 9)

1. Решите систему уравнений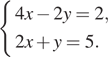

В ответе запишите сумму компонентов решений системы.

2. Решите систему уравнений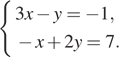

В ответе запишите сумму решений системы.

3. Решите систему уравнений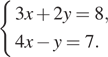

В ответе запишите сумму решений системы.

4. Решите систему уравнений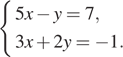

В ответе запишите сумму решений системы.

5. Решите систему уравнений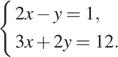

В ответе запишите сумму решений системы.

6. Решите систему уравнений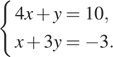

В ответе запишите сумму решений системы.

 

Графический способ применим к решению любой системы, но с помощью графиков уравнений можно приближенно находить решения системы. Лишь некоторые найденные решения системы могут оказаться точными. В этом можно убедиться, подставив их координаты в уравнения системы.

1 Окружность, изображенная на рисунке, задается уравнением 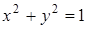. Используя этот рисунок, для каждой системы уравнений укажите соответствующее ей утверждение.

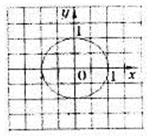А) 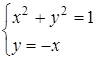             1) Система имеет одно решение

Б) 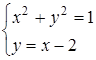              2) Система имеет два решения

В) 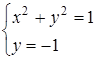             3) Система не имеет решений

 

А	Б	В

Ответ:

 

 

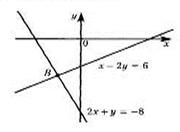
2. Вычислите координаты точки В.

 

 

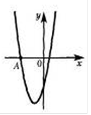
3. На рисунке изображен график функции 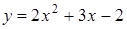. Вычислите абсциссу точки А.