Если система состоит из двух уравнений второй степени с двумя переменными, то найти ее решения обычно бывает трудно. В отдельных случаях такие системы удается решить, используя способ подстановки или способ сложения.
1. Решим систему уравнений

Решение: Выразим из второго уравнения переменную x через y: 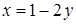 .
.
Подставим в первое уравнение вместо x выражение  , получим уравнение с переменной y:
, получим уравнение с переменной y:
 .
.
После упрощения получим равносильное уравнение
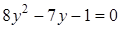 .
.
Решив его, найдем, что  ,
,  . Подставив в формулу
. Подставив в формулу 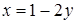
 , получим:
, получим:  .
.
Подставив в формулу 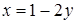 ;
;  , получим:
, получим:
 .
.
И так, система имеет два решения:
 ,
,  и
и  ,
,  .
.
Ответ можно записать также в виде пар:  ,
,  .
.
2. Решим систему уравнений

Решение: Т.К.  , выразим из второго уравнения переменную y через x:
, выразим из второго уравнения переменную y через x:  .; Подставим в первое уравнение вместо y выражение
.; Подставим в первое уравнение вместо y выражение  .
.
Получим уравнение относительно x:  .
.  ,
,  .
.
По формуле  находим y:
находим y:
 ,
,  .
.
Значит, система имеет два решения:
 ,
,  и
и  ,
,  .
.
Ответ:  ,
,  .
.
Решите системы уравнений
1) 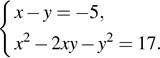
2) 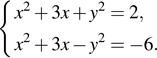
3) 
4) 
5) 
6) 
7) 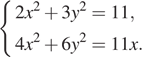
8) 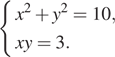
 2020-05-11
2020-05-11 103
103







