2020-05-11
851
Установим теперь, как и при каких условиях можно определить спектральную плотность непрерывного сигнала X(jω) через его отсчеты в дискретные моменты времени, т. е. через значения дискретного сигнала xд(n) = xд(nTд). Для этого запишем общее выражение для спектральной плотности МИП — модели дискретного сигнала в непрерывном времени:
Подставляя выражение для МИП (1.3), получаем:
Откуда, с учетом «фильтрующего свойства» δ-функции, окончательно приходим к соотношению:
Это выражение называется прямым дискретным по времени преобразованием Фурье (ДВПФ).
Раскладывая экспоненты по формуле Эйлера, нетрудно показать, что для вещественных последовательностей:
т.е. спектральная плотность амплитуд вещественной последовательности является четной, а спектральная плотность фаз — нечетной функцией частоты.
При выполнении условий теоремы отсчетов спектральная плотность Xи(jω) в основной полосе (–π/Tд ≤ ω ≤ π/Tд) совпадает с точностью до множителя 1/Tд со спектром непрерывного сигнала, что позволяет рассчитать последний через отсчеты:
|
|
|
Обратное ДВПФ получается из формулы обратного преобразования Фурье подстановкой t = nTд:
При выполнении условий теоремы уиттекера — котельникова — шеннона бесконечные пределы интегрирования можно заменить на конечные.
А спектральную плотность непрерывного сигнала — на спектральную плотность МИП. В результате получим выражение для обратного ДВПФ в виде
Обратим внимание на то, что в выражениях ДВПФ (1.21) и (1.25) спектральная плотность дискретного сигнала остается непрерывной функцией частоты и может быть вычислена через дискретные отсчеты.
Отметим также, что выражения (1.23) и (1.25) справедливы только для сигналов с ограниченным спектром, в то время как (1.21) справедливо всегда, в том числе и при наличии эффекта наложения.
Рассмотрим теперь особенности спектрального представления сигнала, заданного на конечном интервале наблюдения, длительностью T. После дискретизации такой сигнал x д(n) на отрезке [0, T ] представляется конечным числом отсчетов: x (0), x (1),..., xN – 1, взятых через интервал дискретизации T д. Полное число отсчетов N = T / T д. Считается, что никакой другой информации о спектральных свойствах сигнала x д(n), кроме этих отсчетов, нет (рис. 1.4, а).
Методика изучения таких дискретных сигналов — искусственная периодизация с последующим разложением в ряд Фурье дискретного периодического сигнала, точнее, его модели — модулированной импульсной последовательности (рис. 1.4, б).
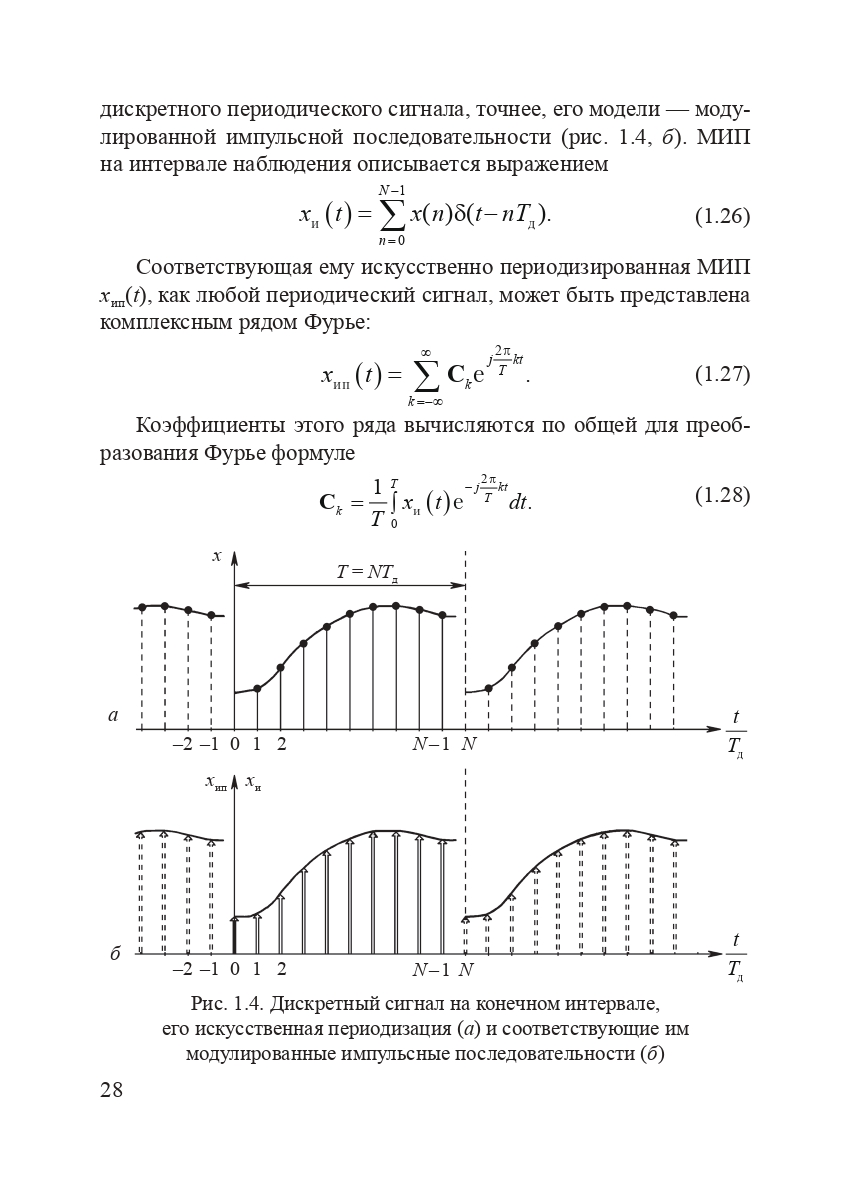
МИП на интервале наблюдения описывается выражением
|
|
|
Соответствующая ему искусственно периодизированная МИП x ип(t), как любой периодический сигнал, может быть представлена комплексным рядом Фурье:
Коэффициенты этого ряда вычисляются по общей для преобразования Фурье формуле
В этом выражении на интервале интегрирования периодическая МИП совпадает с непериодической. Поэтому, подставляя в (1.28) выражение (1.26), получим:
Откуда, с учетом «фильтрующего» свойства δ-функции, получаем:
В этом выражении связь с временным масштабом определяет только сомножитель 1/ T.
Рис. 1.4. дискретный сигнал на конечном интервале, его искусственная периодизация (а) и соответствующие им модулированные импульсные последовательности (б)
Прямым дискретным преобразованием Фурье (ДПФ) называют выражение
Сравнивая два последних выражения, приходим к выводу, что коэффициенты ДПФ X (k) — это коэффициенты разложения в ряд Фурье периодического импульсного сигнала (МИП), площади импульсов которого равны x (n).
Обратное дискретное преобразование Фурье (ОДПФ)определяется выражением
где ядро преобразования обозначено как
Справедливость (1.32) доказывается путем прямой подстановки в него выражения прямого ДПФ:
Внутренняя сумма представляет собой сумму N членов геометрической прогрессии, поэтому
что и превращает выражение (1.33) в тождество.
Отметим основные свойства ДПФ:
1. Линейность преобразования.
Коэффициенты ДПФ дискретной последовательности y (n) = = ax 1(n) + by 1(n) определяются суммой ДПФ коэффициентов: Y (k) = a X 1(k) + b X 2(k).
2. Периодичность коэффициентов ДПФ.
Число различных коэффициентов X (k) равно числу отсчетов дискретного сигнала за период N, ибо функция W N–kn периодична по k с периодом N. Поэтому X (N) = X (0), X (N + 1) = X (1),..., X (k 1 + N) = X (k 1), k 1 < N.
При этом коэффициент X (0)— постоянная составляющая, представляет собой среднее значение по всем отсчетам:
3. Симметрия коэффициентов ДПФ.
Если x (n) — вещественная последовательность, то коэффициенты ДПФ, номера которых симметричны относительно N /2, образуют комплексно-сопряженные пары. Для доказательства этого свойства запишем выражение для коэффициента ДПФ с номером N – k:
С учетом того, что W N–Nn = 1, получаем:
То есть
4. ДПФ сдвинутой последовательности.
Если y (n)— последовательность, образованная путем сдвига периодической (с периодом N) последовательности x (n) на m отсчетов (m < N), то ее ДПФ-коэффициенты
действительно:
Произведя замену переменных n 1 = n + m и учитывая, что x (n 1) W N–kn 1 — периодическая последовательность с периодом N,получаем:
5. ДПФ симметричной последовательности.
Если x (n) = x (N – n), т. е. дискретная последовательность образована путем дискретизации четной функции времени, то ее ДПФ коэффициенты являются вещественными. (доказывается путем представления W N–kn + W Nkm по формуле Эйлера.)
6. Сдвиг коэффициентов ДПФ.
Определим, какой дискретной последовательности соответствуют коэффициенты ДПФ, сдвинутые по частоте на l отсчетов:
Таким образом, коэффициенты ДПФ, сдвинутые по частоте на l отсчетов, соответствуют дискретной последовательности, умноженной на W Nkn.
Такая последовательность образуется в результате операции цифрового гетеродинирования:
y (n) = x (n) W N–nl. (1.38)
7. ДПФ круговой, или циклической свертки двух последовательностей.
Круговой, или циклической сверткой двух периодических (с периодом N)дискретных последовательностей x (n)и h (n)называется последовательность y (n), образованная следующим образом:
Последовательность y (n) — периодическая, с тем же периодом.
Выражение для коэффициентов ДПФ циклической свертки найдем через соответствующие обратные ДПФ:
Подставив (1.40) и (1.41) в (1.39), получим:
Поскольку
То
Откуда следует, что
т.е. ДПФ циклической свертки равно произведению соответствующих коэффициентов ДПФ.
|
|
|
Последнее свойство является очень важным для цифровой обработки сигналов, поскольку позволяет использовать ДПФ для вычисления реакции на выходе цифрового фильтра, которая, как будет показано ниже, описывается линейной сверткой входной последовательности и импульсной характеристики фильтра.
В заключение установим связь между спектральной плотностью непериодического аналогового сигнала X (j ω), спектральной плотностью МИП X и(j ω) и коэффициентами ДПФ X (k).
Коэффициенты разложения в ряд Фурье периодического сигнала определяются значениями спектральной плотности соответствующего непериодического сигнала на частотах, кратных частоте повторения. В частности, для модели дискретного сигнала — периодической МИП:
Как показано при определении ДПФ, коэффициенты разложения в ряд Фурье периодического импульсного сигнала (искусственно периодизированной МИП) вычисляются по формуле
Из сопоставления этого выражения с выражением для коэффициентов ДПФ (1.31) следует, что коэффициенты ДПФ представляют собой отсчеты спектральной плотности непериодической МИП на частотах, кратных 2 π/ T:
Откуда с учетом выражения (1.10) получаем связь между коэффициентами ДПФ и спектральной плотностью аналогового сигнала:
Приведенные соотношения проиллюстрированы на рис. 1.5.
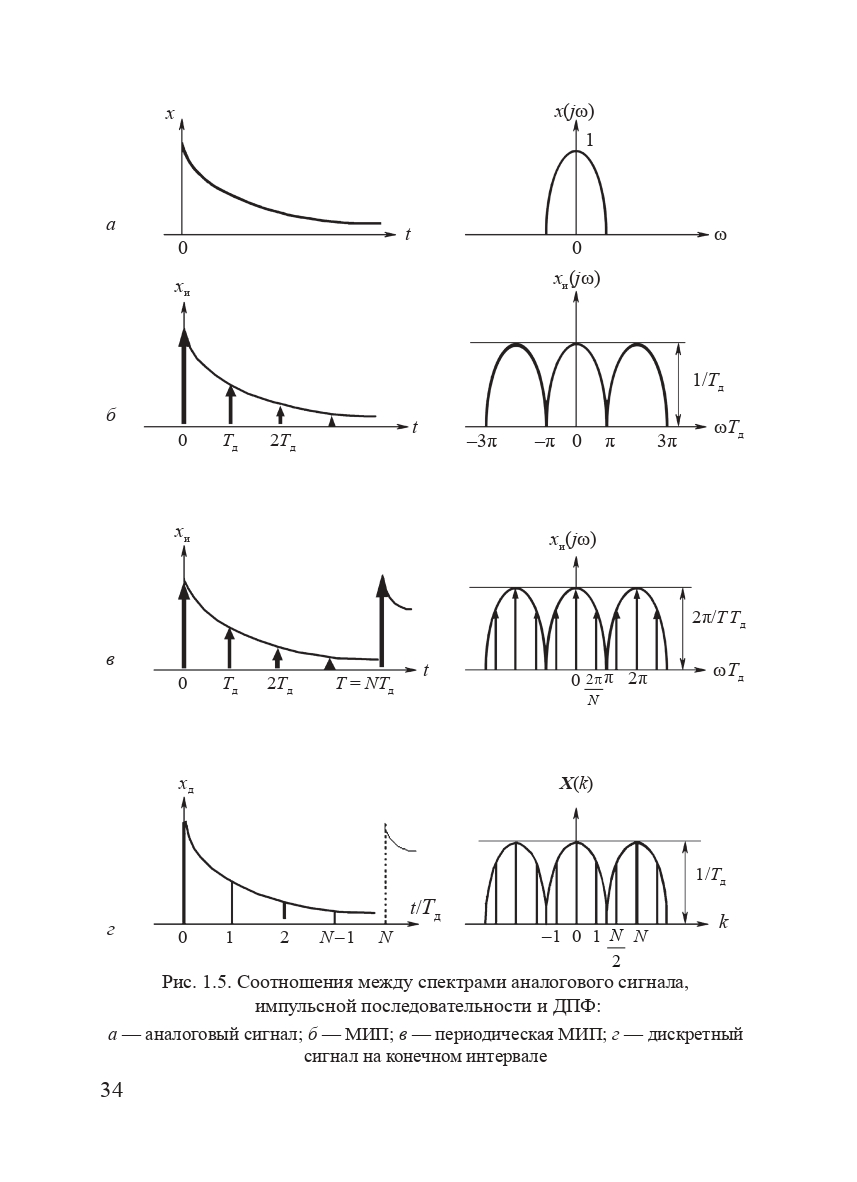
Рис. 1.5. соотношения между спектрами аналогового сигнала, импульсной последовательности и ДПФ: а — аналоговый сигнал; б — МИП; в — периодическая МИП; г — дискретный сигнал на конечном интервале
