Линейные конгруэнтные генераторы

На практике используют более сложные программные генераторы. В большинстве современных программных генераторов используется свойство конгруэнтности, которое заключается в том, что два целых числа  и 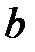 называются конгруэнтными по модулю , если их разность  является числом, которое делится на  без остатка (т.е. является кратным ). Записывается это так:

.

Например, чтобы найти число, конгруэнтное числу 134 по модулю 10, необходимо найти целочисленный остаток от деления 134 на 10, который равен 4, т.е. .

Среди методов генерирования случайных чисел наиболее распространенным является линейный мультипликативный конгруэнтный метод:

                        (1)

где ,  и  – целые числа. Чтобы получить новое число, необходимо взять псевдослучайное число 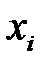 (или задать выходное ), умножить его на коэффициент 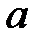, прибавить константу  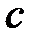и привести полученное число по модулю , т.е. разделить на , и получить остаток. Этот остаток и будет следующим псевдослучайным числом . В случае правильного подбора параметров этот генератор возвращает случайные числа от 0 до .

Полученные по формуле (1) значения  принадлежат диапазону 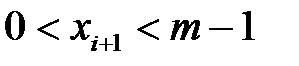 и имеют равномерное дискретное распределение. Для того, чтобы получить случайное значение  из промежутка , необходимо число разделить на . В этом случае все значения 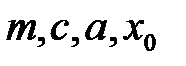 должны быть положительными и удовлетворять условиям: ; . Полученная по формуле (1) последовательность называется линейной конгруэнтной последовательностью.

Одним из недостатков линейных конгруэнтных генераторов является то, что полученные случайные числа  существенно зависят от значений 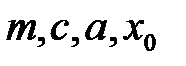 и вычисляются по одной и той же формуле (1), т.е. не являются абсолютно случайными. Но, несмотря на то, что алгоритм их получения является  детерминированным, при условии соответствующего выбора констант  последовательность чисел , на основе которых получают значения , полностью удовлетворяет большинству статистических критериев. Ещё один недостаток этих генераторов заключается в том, что случайные числа , полученные с помощью генератора, могут принимать только дробно-рациональные значения .

Более того, числа  могут принимать лишь некоторые из указанных значений в зависимости от выбранных параметров 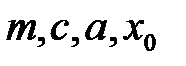, а также от того, как реализуется операция деления чисел с плавающей точкой на число  в компьютере, т.е. в зависимости от типа компьютера и системы программирования. Например, если 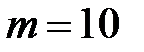, , то получим последовательность 7; 6; 9; 0; 7; 6; 9; 0, которая не является случайной. Это свидетельствует о важности правильного выбора значений констант 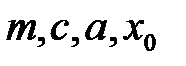. Правильно подобранные значения иногда называют магическими числами.

Конгруэнтная последовательность всегда является циклической, т.е. она начинает повторяться через определенное количество случайных чисел. Количество значений, после которых случайные числа начинают повторяться, называется полным периодом генератора и является основным его параметром. Значения полного периода зависят от разрядности компьютера, а также от значений 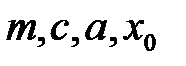. Справедлива теорема, которая определяет условия существования полного периода генератора:

1) Числа  и 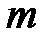 должны быть взаимно простыми;

2)  делилось бы на каждый простой делитель модуля ,

3)  делилось бы на 4, если модуль  кратный 4.

Если , то генератор называется смешанным, а если  – мультипликативным.

Рассмотрим, як нужно выбирать параметры линейного конгруэнтного генератора, чтобы получить последовательность с полным периодом. Для получения такой последовательности нужно выбирать значения , где  – длина разрядной сетки компьютера. Для 32-разрядного компьютера 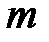 – наибольшее число, которое может быть воспроизведено в нём, данное число равно  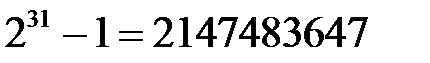(один разряд отводится под знак числа). В этом случае деление  выполнять не обязательно. Если в результате работы генератора будет получено , которое больше чем то, которое может быть воспроизведено в компьютере, возникнет переполнение разрядной сетки. Это приведет к потере крайних левых двоичных знаков целого числа, которые превышали допустимый размер. Однако, разряды, которые остались, являются значениями . Таким образом, при генерировании вместо операции деления можно воспользоваться переполнением разрядной сетки.

По поводу константы  теорема утверждает, что для получения последовательности с полным периодом генератора значение  должно быть нечетным, и, кроме того,  должно делиться на 4. Для такого генератора начальное значение  может быть произвольным и находиться в диапазоне от 0 до . Если , то получим мультипликативный конгруэнтный метод, который предусматривает применение рекуррентных выражений:

                     (2)

Этот метод более скоростной, чем предыдущий, однако, не даёт последовательности с полным периодом. Действительно, из выражения (2) видно, что значение  может появиться в том случае, если последовательность вырождается в нуль. Вообще, если  – любой делитель  и  кратно , все следующие элементы мультипликативной последовательности  будут кратными  Таким образом, если , нужно, чтобы  и  были взаимно простыми числами с  и находились между 0 и

Что касается выбора , то в случае, когда , где 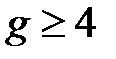, имеем  или 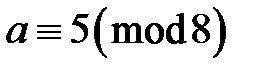. В этом случае четвертая часть всех возможных значений множителей даёт длину периода, равную , который и будет максимальным периодом генератора.

Существуют и другие конгруэнтные методы генерирования случайных чисел, среди которых следует отметить аддитивный.

Наипростейший генератор, последовательность которого  зависит более чем от одного из предыдущих значений - это генератор, который использует числа Фибоначчи:

.

Этот генератор широко использовался в 50-е годы ХХ столетия, но, как показали дальнейшие исследования, статистические свойства его достаточно низкие.

Рассмотренные методы генерирования случайных чисел не касаются исследований, которые используют языки или пакеты моделирования. Эти средства содержат встроенные генераторы случайных чисел, качество которых зависит от разработчиков этих программных средств.