Составим и решим симплексным методом задачу, двойственную задаче об использовании сырья, сформулированной в 2.4 (см. пример 4). Экономико-математическая модель формулируется так: найти максимум функции F= 6х1 + + 2х2 + 2,5х3 + 4х4, выражающей прибыль предприятия, при следующих ограничениях:

Решение задачи симплексным методом привело к следующему результату: максимальное значение функции F, равное 1050 ден. ед., достигается при оптимальном решении (0, 225, 0, 150, 475, 0, 0). Первые четыре компоненты этого решения дают оптимальный план выпуска продукции, а последние три -остатки сырья видов I, II и III.
Рассмотрим эту задачу как исходную и составим двойственную ей. Матрица В условий прямой задачи и матрица В’ - транспонированная матрица В - имеют следующий вид:
| 5 | 1 | 0 | 2 | 1000 | 5 | 4 | 1 | 6 | |||
| B= | 4 | 2 | 2 | 1 | 600 | B’= | 1 | 2 | 0 | 2 | |
| 1 | 0 | 2 | 1 | 150 | 0 | 2 | 2 | 2.5 | |||
| 6 | 2 | 2.5 | 4 | Fmax | 2 | 1 | 1 | 4 | |||
| 1000 | 600 | 150 | Zmin |
В двойственной задаче нужно найти минимум функции
Z = 1000y1 + 600y2 +150,
при ограничениях 
Систему ограничений-неравенств двойственной задачи обратим в систему уравнений: 
Применив теперь алгоритм симплекс-метода, решим поставленную задачу: Zmin= 1050. Оптимальное решение (0; 1; 3; 1; 0; 5.5; 0).
Запишем соответствующие переменные прямой и двойственной задач:
x1 x2 x3 x4
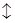 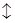 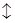 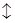 y4 y5 y6 y7
y4 y5 y6 y7
| x5 x6 x7
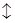 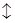 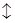 y1 y2 y3
y1 y2 y3
|
Компоненты у1, у2, у3 оптимального решения двойственной задачи оценивают добавочные переменные х5, х6, х7 прямой задачи.
Равенство нулю переменной у1 в оптимальном решении свидетельствует о том, что переменная х5 положительна в оптимальном решении прямой задачи, или что подстановка компонент оптимального решения в первое неравенство системы ограничений прямой задачи не обращает его в строгое равенство.
Переменные у2, у3 положительны, а соответствующие им переменные прямой задачи х6, х7 равны нулю в оптимальном решении прямой задачи. Подстановка компонент оптимального решения во второе и третье неравенства прямой задачи обращает их в строгие равенства.
Экономический смысл этого обстоятельства состоит в том, что сырья вида I у нас имеется с излишком и мы не особенно «дорожим» им, поэтому устанавливаем для него нулевую оценку, а вот сырье видов II и III является дефицитным, оно все целиком расходуется, поэтому мы оцениваем эти виды сырья некоторыми положительными оценками (у2 = 1, у3 = 3).
Как оценить единицу сырья каждого вида в зависимости от той прибыли, которую приносит предприятию реализация продукции А1, А2, А3, А4? Подчеркнем, что речь идет не о стоимости сырья при его приобретении предприятием. Нас интересует относительная стоимость сырья с точки зрения получения максимальной прибыли при изменении его запасов. Ясно, что ценность того или иного вида сырья будет определяться величиной роста максимальной прибыли при увеличении, например запаса сырья i-го вида.
Cогласно выводу из теоремы об оценках DFmax = yiDbi.
В этой формуле уi -компонента оптимального решения двойственной задачи. Здесь особенно ощутимо видна стоимостная сущность переменных двойственной задачи. Они выступают как условные цены единицы i-го вида сырья. Поэтому переменные двойственной задачи часто называют объективно обусловленными оценками.
Вернемся к оптимальному плану двойственной задачи. При этом нас будут интересовать только первые три компоненты: у1 = 0, у2 = 1, у3 = 3 этого решения, которые соответствуют добавочным переменным прямой задачи х5, х6, х7, выражающим величины остатков сырья видов I, II, III.
Ответим на вопрос: как изменится оптимальный план выпуска продукции, а вместе с ним и максимальная прибыль, если увеличивать запасы сырья каждого вида?
Пусть запас сырья вида I увеличился на 100 усл. ед. Пользуясь формулой (5.3), получим
DFmax = y1Db1 = 0*100 = 0,
т. е. прибыль не увеличится, оптимальное решение не изменится. Последний вывод закономерен, ибо выпуск продукции в условиях прямой задачи лимитируется наличием сырья видов II, III.
Увеличим на 100 ед. запас сырья вида II. Тогда
DFmax = y2*100 = 1*100 = 100 ден. ед.
Решая прямую задачу симплексным методом (рекомендуется сделать самостоятельно) с измененной правой частью второго ограничения-неравенства: 4х1 + 2х2 + 2х3 + х4 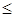 700, получим оптимальное решение
700, получим оптимальное решение
(0, 275, 0, 150, 425, 0; 0).
Увеличив на 100 усл. ед. запас сырья III, получим
DFmax = y3*100 = 3*100 = 300 ден. ед.
При этом измененном условии максимальная прибыль равна 1350 усл. ед. при оптимальном плане (0, 175, 0, 250, 325, 0, 0). В справедливости последнего утверждения можно убедиться, решив симплексным методом прямую задачу с измененной правой частью третьего ограничения-неравенства: х1 + 2х3 + х4 £ 250.
 2020-05-11
2020-05-11 214
214








