Примеры решения заданий

Пусть необходимо найти оптимальный план производства двух видов продукции Р и R, то есть такой план, при котором целевая функция (общая прибыль) была бы max, а имеющиеся ресурсы использовались бы наилучшим образом.

Таблица 2.1

Данные о запасе и нормах расхода ресурсов

Типы ресурсов	Норма расхода ресурса на ед.		Объем ресурса (запасы)
	P	R
A	2	1	12
B	0,1	0,5	4
C	3,5	1	18
Прибыль на ед. изделия	4	5	-

Требуется:

I. Cформулировать экономико-математическую модель задачи в виде ОЗЛП.

II. Привести ОЗЛП к канонической форме.

III. Сформулировать экономико-математическую модель задачи двойственной к исходной.

IV. Построить многогранник решений (область допустимых решений) и найти оптимальную производственную программу путем перебора его вершин и геометрическим способом.

V. Решить задачу с помощью симплекс-таблиц.

Решение:

I. Оптимизационная модель задачи запишется следующим образом:

а) целевая функция

б) ограничения:

в) условия неотрицательности переменных х₁≥0; х₂≥0.

II. Приведем ОЗЛП к канонической форме. Для этого введем дополнительные переменные x ₃, x ₄ и x ₅.

а) целевая функция

б) ограничения:

в) условия неотрицательности переменных .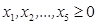

III. Сформулируем экономико-математическую модель задачи двойственную к исходной. Матрица В условий прямой задачи и матрица В’ – транспонированная матрица В – имеют следующий вид:

	2	1	12			2	0,1	3,5	4
B=	0,1	0,5	4		B’=	1	0,5	1	1
	3,5	1	18			12	14	18	Zmin
	4	1	Fmax

В двойственной задаче нужно найти минимум функции

Z = 12y₁ + 14y₂ +18y₃, при ограничениях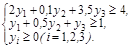

Систему ограничений-неравенств двойственной задачи обратим в систему уравнений:

Компоненты у₁, у₂, у₃ оптимального решения двойственной задачи оценивают добавочные переменные х₃, х₄, х₅ прямой задачи.

VI. Построим многогранник решений (область допустимых решений) и найдем оптимальную производственную программу путем перебора его вершин и геометрическим способом.

Преобразуем нашу систему ограничений, найдя в каждом из уравнений х₂ и отложим их на графике. Любая точка на данном графике с координатами х₁, х₂ представляет вариант искомого плана. Однако ограничения по ресурсу А сужают область допустимых решений. Ими могут быть все точки, ограниченные осями координат и прямой, так как не может быть израсходовано ресурса больше, чем его на предприятии имеется. Если точки находятся на самой прямой, то ресурс используется полностью. Аналогичные рассуждения можно привести для ресурсов В и С. В результате условиям задачи будет удовлетворять любая точка лежащая в пределах заштрихованного многоугольника. Данный многоугольник называется областью допустимых решений.

Определим точки пересечения линий ограничений с осями:

1) : (0;12) и (6; 0);

2) 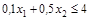: (0; 8) и (40; 0);

3) 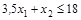: (0; 18) и (5,14; 0);

Однако нам необходимо найти такую точку, в которой достигался бы max целевой функции.

Оптимальную производственную программу можно найти двумя способами:

1) путем перебора его вершин

Находим координаты вершин многоугольника ABCDE и подставляя в целевую функцию находим ее значение.

А: А (0; 0)          Z(A) =4×0+5×0=0

В: В (0; 8)          Z(B) = 4×0+5×8=40

С: – это пересечение первого и второго уравнений

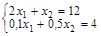; ; -9 x ₂=-68 x ₂=7,555; x ₁=2,222.

С (2,22; 7,55)     Z(C) = 4×2,22+5×7,55=8,88+37,77=46,65

 

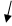
D: – это пересечение первого и третьего уравнений

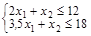; 1,5 x ₁=6; x ₁=4; x ₂=4.

D (4; 4)                Z(D)=4×4+5×4=20+25=45

E: (5,14; 0)         Z(E) = 4×5,14+5×0=20,56

Находим max значение целевой функции. Оно находится в точке
С (2,22; 7,55). Таким образом max прибыль составит 46,65 у.д.е. при выпуске продукта Р в количестве 2,22 у.е. и R – 7,55 у.е.

2) геометрическим способом

Целевая функция геометрически изображается с помощью прямой уровня, т.е. прямой на которой Z=C₀+C₁X₁+C₂X₂ – принимает постоянное значение.

Если С – произвольная const, то уравнение прямой имеет вид

C₀+C₁X₁+C₂X₂=С

При изменении const С получаем различные прямые, параллельные друг другу. При увеличении С прямая уровня перемещается в направлении наискорейшего возрастания функции Z, т.е. в направлении ее градиента. Вектор градиента

Точкой min Z будет точка первого касания линии уровня с допустимым многоугольником. Точкой max – точка отрыва линии уровня от допустимого многоугольника. Эти точки чаще всего совпадают с некоторыми вершинами допустимого многоугольника, хотя их может быть и бесчисленное множество, если линия уровня Z параллельна одной из сторон допустимого многоугольника. Это точка С (2,22; 7,55)

Z=46,65 у.д.е.

VII. Решим задачу с помощью симплекс-таблиц.

Пусть необходимо найти оптимальный план производства двух видов продукции P и R.

1. Построим оптимизационную модель:

F(X)=4X₁+5X₂→max                  

1. Преобразуем задачу в приведенную каноническую форму. Для этого введем дополнительные переменные X₃, X₄ и X₅.

F(X)=4X₁+5X₂→max                  

Построим исходную симплекс-таблицу и найдем начальное базисное решение.

Баз. пер.	Своб. член	Х1	Х2	Х3	Х4	Х5
Х3	12	2	1	1	0	0
Х4	4	0,1	0,5	0	1	0
Х5	18	3,5	1	0	0	1
F	0	– 4	– 5	0	0	0

Базисное решение (0; 0; 12; 4; 18). F=0.

Находим генеральный столбец и генеральную строку

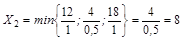. Генеральный элемент 0,5.

Баз. пер.	Своб. член	Х1	Х2	Х3	Х4	Х5
Х3	4	1,8	0	1	2	0
Х2	8	0,2	1	0	2	0
Х5	10	3,3	0	0	-2	1
F	40	– 3	0	0	-10	0

Базисное решение (0; 8; 4; 0; 10). F=40.

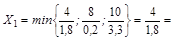2,22222. Генеральный элемент 1,8.

Баз. пер.	Своб. член	Х1	Х2	Х3	Х4	Х5
Х1	2,22	1	0	0,55	1,11	0
Х2	7,56	0	1	-0,11	1,77	0
Х5	2,74	0	0	1,82	5,63	1
F	46,65	0	0	-1,665	-13,3	0

Базисное решение (2,22; 7,56; 0; 0; 2,74). F=46,65.

Эта таблица является последней, по ней читаем ответ задачи. Оптимальным будет решение (2,22; 7,56; 0; 0; 2,74), при котором F_max =46,65, т.е. для получения наибольшей прибыли, равной 46,65 денежных единиц, предприятие должно выпустить 2,22 единиц продукции вида P и 7,56 единиц продукции вида R, при этом ресурсы A и B будут использованы полностью, а 2,74 единиц ресурса С останутся неизрасходованными.