Лекция 7
СТРУКТУРНЫЙ АНАЛИЗ СЛУЧАЙНЫХ ПРОЦЕССОВ
Задачи структурного анализа
Рассмотрим некоторую реализацию 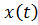 случайного процесса (рис. 4.1).
случайного процесса (рис. 4.1).
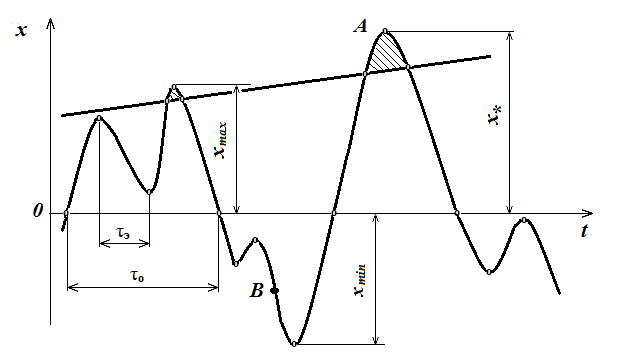
Рис. 4.1
Отметим на ней характерные точки, соответствующие им значения процесса и интервалы времени между ними:
- точки пересечения среднего (нулевого) уровня, называемые нулями процесса;
- точки, соответствующие экстремальным значениям процесса, которые называются экстремумами процесса;
- точку А, соответствующую наибольшему для данной реализации максимуму процесса, называемую абсолютным максимумом процесса;
- точку В, соответствующую перегибу траектории процесса, называемую точкой перегиба;
- точки пересечения случайного процесса с некоторым уровнем, определяющие число превышений (выбросов) за этот уровень;
- интервалы времени 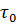 между двумя соседними нулями, от которых зависит частота процесса, рассчитанная по пересечениям нулевого уровня (частота по нулям);
между двумя соседними нулями, от которых зависит частота процесса, рассчитанная по пересечениям нулевого уровня (частота по нулям);
- интервал времени 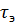 , которые соответствуют двум соседним экстремумам, определяющие частоту процесса по экстремумам;
, которые соответствуют двум соседним экстремумам, определяющие частоту процесса по экстремумам;
- отрезки 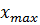 и
и 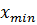 между нулевой линией и соответствующим экстремумом, называемые экстремальными значениями процесса (максимумом и минимумом);
между нулевой линией и соответствующим экстремумом, называемые экстремальными значениями процесса (максимумом и минимумом);
- отрезок 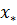 между нулевой линией и наибольшим максимумом процесса, называемый значением абсолютного максимума;
между нулевой линией и наибольшим максимумом процесса, называемый значением абсолютного максимума;
- приращение процесса 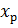 между двумя соседними экстремумами, называемое размахом процесса.
между двумя соседними экстремумами, называемое размахом процесса.
Получение вероятностной информации о количестве указанных выше точек за некоторый промежуток времени и о величинах указанных выше отрезков по заданным вероятностным характеристикам процессов (по корреляционным функциям или энергетическим спектрам) является задачей структурного анализа случайных процессов.
Нули, выбросы, перегибы траектории и другие особые точки случайного процесса
Число пересечений нулевого уровня (число нулей) некоторой функции 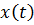 в течение времени
в течение времени 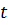 можно найти по формуле (функционал Стайнберга)
можно найти по формуле (функционал Стайнберга)
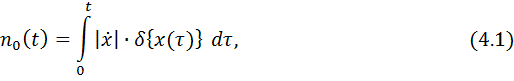
где 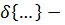 дельта-функция.
дельта-функция.
Поскольку при дифференцировании функции ее экстремумы переходят в нули, то из (4.1) число экстремумов функции 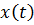 за время
за время 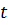 можно найти по формуле
можно найти по формуле

Число точек перегиба траектории, в которых вторая производная равна нулю:
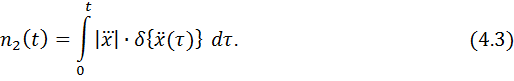
Обобщив соотношения (4.1) – (4.3), получим следующее выражение для нахождения числа особых точек траектории функции 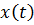 , в которых ее
, в которых ее 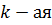 по счету производная равна нулю:
по счету производная равна нулю:
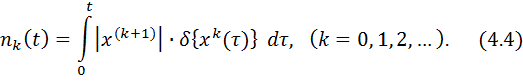
В случае, когда 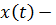 случайная функция, для определения вероятностных характеристик числа особых точек следует ввести соответствующие функции распределения вероятностей случайных величин и рассмотреть приведенные выше соотношения как функции случайных аргументов. Так, если через
случайная функция, для определения вероятностных характеристик числа особых точек следует ввести соответствующие функции распределения вероятностей случайных величин и рассмотреть приведенные выше соотношения как функции случайных аргументов. Так, если через 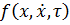 обозначить плотность совместного распределения вероятностей функции
обозначить плотность совместного распределения вероятностей функции 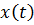 и ее производной для некоторого момента времени
и ее производной для некоторого момента времени 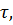 среднее число нулей этой функции за время t
среднее число нулей этой функции за время t
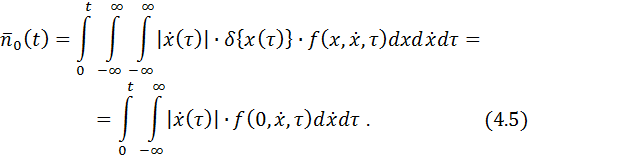
Определение числа превышений процессом 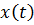 некоторого уровня х сводится к определению числа нулей разности
некоторого уровня х сводится к определению числа нулей разности 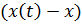 . Если случайная функция
. Если случайная функция 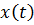 стационарна, из (4.5) получаем следующее выражение для нахождения среднего числа превышений процессом
стационарна, из (4.5) получаем следующее выражение для нахождения среднего числа превышений процессом 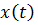 уровня х в единицу времени:
уровня х в единицу времени:

При этом среднее число пересечений нулевого уровня (т.е. среднее число нулей) в единицу времени
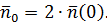
По аналогии с (4.6) получаем выражения для определения среднего числа экстремумов и точек перегиба траектории в единицу времени:
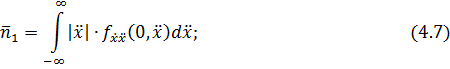
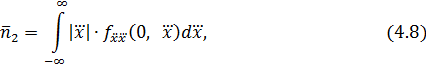
где 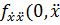 ) - плотность совместного распределения вероятностей первой и второй производных при
) - плотность совместного распределения вероятностей первой и второй производных при 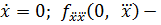 плотность совместного распределения вероятностей второй и третьей производных при
плотность совместного распределения вероятностей второй и третьей производных при 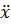 =0.
=0.
Подставив в (4.6) – (4.8) выражения для плотностей распределения вероятностей для Гауссовых стационарных процессов, получим:
- среднее число превышений процессом 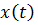 уровня х в единицу времени
уровня х в единицу времени
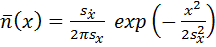 ; (4.9)
; (4.9)
- среднее число пересечений процессом 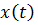 нулевого уровня в единицу времени
нулевого уровня в единицу времени

- среднее число экстремумов процесса 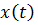 в единицу времени
в единицу времени

- среднее число точек перегиба процесса 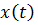 в единицу времени
в единицу времени

где 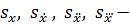 средние квадратические отклонения процесса и его первых трех производных соответственно.
средние квадратические отклонения процесса и его первых трех производных соответственно.
Сложность структуры случайного процесса характеризуется отношением числа экстремумов к числу нулей

Для процесса простой структуры 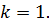
 2020-05-11
2020-05-11 413
413







