Миноры. Алгебраические дополнения. Обратная матрица

 

1. Минором М_ij элемента a_ij называется определитель, составленный из элементов, оставшихся после вычеркивания i-ой стоки и j-го столбца, на пересечении которых находится этот элемент.

Пример 1. Пусть А= , тогда  =

Этот минор получается из A путём вычёркивания второй строки и третьего столбца.

Пример 2. Пусть дана матрица А= 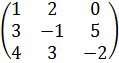. Найдем её миноры.

М₁₂= = - 6 - 20= - 26

 

М₃₁₌₌ = 10-0= 10

 

2. Алгебраическим дополнением А_ij элемента a_ij называется минор М_ij этого элемента, взятый со знаком (. А_ij =( _ij

Пример 1.. Пусть дана матрица А= 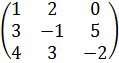. Найдем её алгебраические дополнения некоторых элементов.

А₂₂ = = 1  (-2-0) = -2

А₁₂=  = -1  (-6-20) = 26

 

3.  Обратная матрица - матрица, для которой выполняется равенство:

 А А^-1=Е, где А^-1- обратная матрица, Е- единичная матрица.

 Алгоритм нахождения обратной матрицы:

1. Вычислить определитель матрицы А.

2. Вычислить все алгебраические дополнения и записать из них матрицу А^*.

3. Транспонировать матрицу А^*, записать матрицу А^*т.

4. Умножить полученную матрицу на .

 

Пример.  Найти обратную матрицу для матриц В=

1) Находим определитель матрицы В: 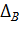= 6-(-4) =10 0, следовательно, обратная матрица существует.

2) Алгебраические дополнения:

А₁₁= 3= 3; А₁₂= 4=-4

А₂₁= (-1)= 1; А₂₂= 2= 2

А^*=

3) записать матрицу А^*т =

4) Записать обратную матрицу: А^-1= =

Пример 2. Найти обратную матрицу для матрицы В =

 

1) Находим определитель матрицы. = -1, следовательно, обратная матрица существует.

2) Матрица из алгебраических дополнений:

В^*=

3) Транспонируем матрицу:

В^*т=

4).Обратная матрица:

В^-1= =

Проверка:

А^-1= =

1. Находим неизвестные, выполняем умножение Х=А^-1В

Х=

Х₁= -  =

Х₂= -  –  =-

 

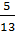
2. Сделаем проверку:

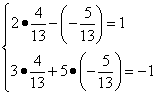
Следовательно, ответ правильный (1; -1)

Решите системы методом Крамера и матричным методом.

1)

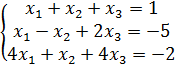
2)

3)

4)

5)

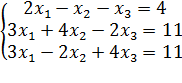
6)

 

 

 Решение систем линейных уравнений методом Гаусса

Метод Гаусса заключается в преобразовании расширенной матрицы к эквивалентной ей матрице ступенчатого вида. Называется по- другому «методом последовательного исключения неизвестных».

Алгоритм решения системы уравнений методом Гаусса:

Пусть дана система линейных уравнений:

 

1) Записать расширенную матрицу

2) Выполнить «прямой ход», привести матрицу к треугольному виду:

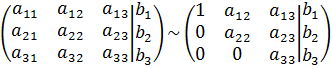
3) Выполнить «обратный ход», записав полученную эквивалентную систему, найти , , .

Во время выполнения «прямого хода» можно выполнять следующие преобразования матрицы:

1) Умножать и делить всю строку (столбец) на одно и то же число, отличное от нуля;

2) Складывать и вычитать уравнения;

3) Менять строчки (столбцы) местами;

4) Отбрасывать нулевую строку (столбец).

Пример.

Запишем расширенную матрицу и выполним её преобразования:

 

 

Записываем эквивалентную систему:

 

Подставим 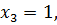 в первое уравнение , .

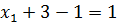Записываем ответ (-1; 3; 1).

Решите системы методом Гаусса:

1)     

2)

3)

4)

5)

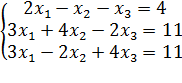
6)

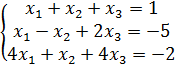
7)

 

 

Выполните задания по темам