ТЕМА: «Формулы половинного угла в тригонометрии».
Список формул половинного угла
Для начала перечислим все формулы половинного угла:
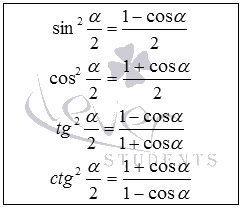
Доказательство формул половинного угла
Из формулы соs2х=соs2 x-sin2 x при х =  получаем cosα = соs2
получаем cosα = соs2  -sin2
-sin2 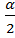 (1)
(1)
Выпишем основное тригонометрическое тождество в виде соs2  +sin2
+sin2  =1(2)
=1(2)
Складывая равенства (1) и (2) получим: 1+ cosα = соs2  -sin2
-sin2  + соs2
+ соs2  +sin2
+sin2 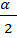 =
=
2 соs2  (3)
(3)
Вычитая из равенства (2) равенство (1) получим: 1- cosα = соs2  +sin2
+sin2  - соs2
- соs2  +sin2
+sin2 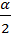 =2 sin2
=2 sin2  (4)
(4)
Из формулы (3) получим: соs2 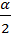 =
= 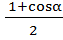 (5)
(5)
Из формулы (4) получим: sin 2 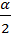 =
= 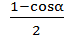 (6)
(6)
Разделим равенство (6) на равенство (5), а затем равенство (5) на равенство (6) получим:
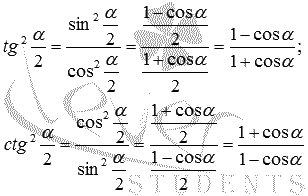
Так мы доказали все формулы половинного угла.
Примеры использования
Пример.
Зная, что 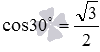 , вычислите при помощи формулы половинного угла значение косинуса 15 градусов.
, вычислите при помощи формулы половинного угла значение косинуса 15 градусов.
Решение.
Формула половинного угла для косинуса имеет вид 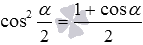 , тогда
, тогда 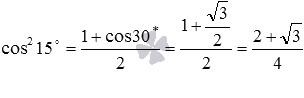 . Итак, значение квадрата косинуса 15 градусов найдено, осталось по нему найти значение самого косинуса.
. Итак, значение квадрата косинуса 15 градусов найдено, осталось по нему найти значение самого косинуса.
Так как угол 15 градусов является углом первой координатной четверти, то косинус этого угла должен быть положительным (при необходимости смотрите раздел теории знаки синуса, косинуса, тангенса и котангенса по четвертям). Таким образом, так как 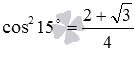 , то
, то 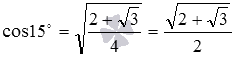 .
.
Ответ:
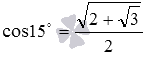 .
.
Обязательно стоит обратить Ваше внимание, что для применения формул половинного угла аргументы не обязательно должны иметь явный вид 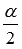 и
и 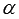 , главное – чтобы аргумент в правой части формул половинного угла был вдвое больше аргумента в левой части формул. К примеру, формула половинного угла для синуса позволяет записать равенство
, главное – чтобы аргумент в правой части формул половинного угла был вдвое больше аргумента в левой части формул. К примеру, формула половинного угла для синуса позволяет записать равенство 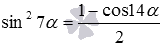 или
или 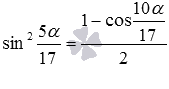 .
.
отдельного рассмотрения.
Пример№2.
Вычислить соs  , если cosα=-0,02 и 0<α<π
, если cosα=-0,02 и 0<α<π
Решение:
соs2  =
= 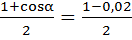 =0,49. Так как 0 < α < π, то 0 <
=0,49. Так как 0 < α < π, то 0 < 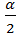 <
< 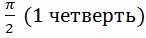 , поэтому соs
, поэтому соs  >0, таким образом соs
>0, таким образом соs 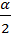 =
= 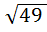 = 7
= 7
Ответ: соs 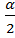 = 7
= 7
Пример№3.
Вычислить tg  , если cosα=0,8 и π <α< 2π.
, если cosα=0,8 и π <α< 2π.
Решение: tg 2 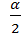 =
= 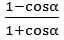 =
= 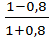 =
= 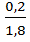 =
= 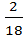 =
= 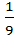 . Так как π <α< 2π, то
. Так как π <α< 2π, то  <
< 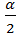 <
< 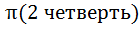 , поэтому tg
, поэтому tg 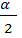 < 0, отсюда tg
< 0, отсюда tg 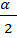 =
= 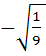 =
=  .
.
Ответ: tg 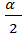 =
=  .
.
Пример№4.
Упростите выражение 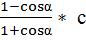 tg 2
tg 2 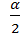 -
- 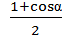
Решение: 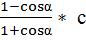 tg 2
tg 2 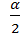 -
- 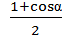 = tg 2
= tg 2 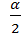 *
* 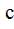 tg 2
tg 2 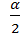 - соs2
- соs2  =1- соs2
=1- соs2  = sin 2
= sin 2 
Ответ: sin 2 
Пример№5.
Вычислить 2соs2  - 1= 2
- 1= 2 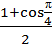 - 1 = 1+
- 1 = 1+ 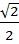 - 1 =
- 1 = 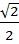
Ответ: 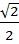
Пример№6.
Вычислить 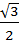 + 2sin 2 150 =
+ 2sin 2 150 = 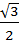 +2
+2 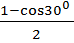 =
= 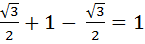
Ответ: 1
Пример№7
Вычислить sin  ,если cosα=0,6 и 2π <α< 3π.
,если cosα=0,6 и 2π <α< 3π.
Решение: sin 2 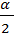 =
= 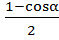
sin 2 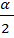 =
= 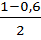 =
= 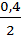 = 0,2. Так как 2π <α< 3π, то
= 0,2. Так как 2π <α< 3π, то 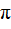 <
< 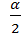 <
< 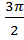 (3 четверть), значит sin
(3 четверть), значит sin 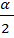 = -
= - 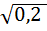
Ответ: - 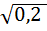
Пример№8
Вычислить соs 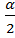 ,если cosα=0,6 и 2π <α< 3π.
,если cosα=0,6 и 2π <α< 3π.
Решение: соs2  =
= 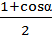
соs2 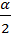 =
= 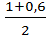 =
= 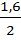 = 0,8. Так как (3 четверть), то соs
= 0,8. Так как (3 четверть), то соs  =
= 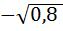
Ответ: - 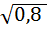
Пример№9
Вычислить tg  ,если cosα=0,6 и 2π <α< 3π.
,если cosα=0,6 и 2π <α< 3π.
Решение: tg 2 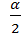 =
= 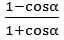 =
= 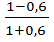 =
= 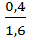 =
= 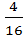 =
= 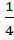 . Так как (3 четверть), то
. Так как (3 четверть), то
tg 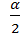 =
=  =
=  .
.
Ответ: 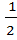
Пример№10
Вычислить сtg  ,если cosα=0,6 и 2π <α< 3π.
,если cosα=0,6 и 2π <α< 3π.
Решение: Так как сtg 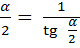 , то сtg
, то сtg 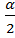 =
= 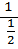 = 2
= 2
Ответ: 2
Пример№11
Упростить выражение: 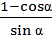
Решение: Так как sin 2 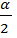 =
= 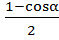 , то 1- cosα = 2 sin2
, то 1- cosα = 2 sin2  , отсюда
, отсюда 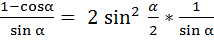 . Пусть
. Пусть 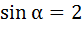 sin
sin 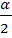 соs
соs  , тогда получим:
, тогда получим: 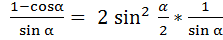 =
= 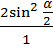 *
* 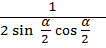 =
= 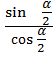 = tg
= tg 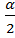
Ответ: tg 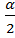
Пример№12
Упростить выражение: 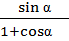
Решение: Так как соs2 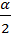 =
= 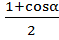 , то 1+ cosα = 2 соs2
, то 1+ cosα = 2 соs2  . Пусть так же
. Пусть так же 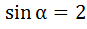 sin
sin 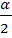 соs
соs  , тогда получим:
, тогда получим: 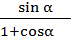 =
= 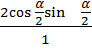 *
* 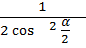 =
= 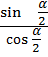 = tg
= tg 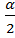
Ответ: tg 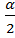
 2020-05-11
2020-05-11 361
361







