а) Выполните заданное число (n) замеров напряжения. В дальнейшем считайте, что систематическая погрешность отсутствует.
б) Определите среднее арифметическое значение
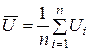
и примите его в качестве действительного значения.
в) Вычислите погрешности замеров
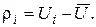
Результат замеров и вычислений оформите в виде таблицы.
г) Определите оценку среднего квадратического отклонения (СКО) погрешности:
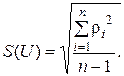
д) Проверьте максимальные и минимальные результаты замеров на наличие грубых погрешностей. Замеры, у которых 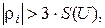 исключаются из рассмотрения, и заново выполняются пункты б...г.
исключаются из рассмотрения, и заново выполняются пункты б...г.
е) Постройте три гистограммы распределения погрешностей замеров для 5, 6, 7 интервалов. Алгоритм построения гистограммы приведен в п. 3.2.
ж) Проверьте гипотезу о том, что результаты наблюдений подчиняются нормальному закону распределения.
В простейшем случае нормальность закона распределения можно оценить по виду гистограмм.
и) Определите оценку СКО результата измерения:
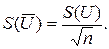
к) Определите доверительные границы ε случайной погрешности при доверительных вероятностях 0,9; 0,95; 0,99.
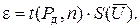
Значения коэффициента Стьюдента 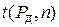 возьмите из таблицы (табл. 2).
возьмите из таблицы (табл. 2).
Таблица 2
| n | P д = 0,9 | P д = 0,95 | P д = 0,99 |
| 10 | 1,83 | 2,26 | 3,25 |
| 16 | 1,75 | 2,13 | 2,95 |
| 25 | 1,71 | 2,06 | 2,80 |
к) Определите доверительные границы погрешности результата измерения. Поскольку систематическая погрешность отсутствует, 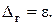
л) Запишите результаты измерения при различных значениях 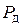 в форме:
в форме: 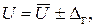
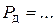
 2020-05-11
2020-05-11 149
149








